Главная | Обратная связь | Поможем написать вашу работу!

Задания и постановка задачи.

Содержание

1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 2. 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 3. 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8

Введение.................................................................................................... Вычисление значения интеграла функции, заданной графически…... Постановка задачи...................................……………………………….. Математическая формулировка задачи................................................. Численный метод решения..................................................................... Инструкция программисту..................................................................... Схема алгоритма....................................................................................... Текст программы..................................................................................... Инструкция пользователю...................................................................... Тестовый пример.................................................................................... Составление таблицы значений функции, заданной в виде разложения в ряд..................................................................................... Постановка задачи...............................................................…………….. Математическая формулировка задачи................................................... Численный метод решения....................................................................... Инструкция программисту....................................................................... Схема алгоритма........................................................................................ Текст программы....................................................................................... Инструкция пользователю........................................................................ Тестовый пример....................................................................................... Работа с матрицами................................................................................... Постановка задачи...................................................…………………….. Математическая формулировка задачи................................................... Численный метод решения....................................................................... Инструкция программисту....................................................................... Схема алгоритма........................................................................................ Текст программы....................................................................................... Инструкция пользователю........................................................................ Тестовый пример....................................................................................... Вывод..........................................................................................................

4 5 5 6 7 9 10 10 13 13 16 16 17 17 18 19 22 22 22 26 26 28 28 28 29 32 35 36 37

Введение

В данной контрольно-курсовой работе требуется применить изученные средства языка программирования Паскаль для решения математических задач путем использования численных методов на компьютере.

Необходимо написать три программы, решающие поставленные задачи, используя предоставленные математические обоснования. Решение данных задач показывает возможности использования компьютера для различного рода прикладных вычислений.

В первой задаче требуется разработать алгоритм и его реализацию для нахождения интеграла функции, заданной графически. Ценность данной задачи заключается в том, что не для каждой функции значение интеграла можно найти аналитически. Однако с использованием предложенного численного метода, возможно, получить конкретное значение с достаточной требуемой точностью.

Во второй задаче необходимо составить алгоритм и реализацию данного алгоритма, который позволит напечатать таблицу значений функции, заданной в виде разложения в ряд. Без использования компьютера процесс вычисления значений такой функции занимает достаточно длительное время. Компьютер же дает возможность значительно ускорить этот процесс, что позволяет, например, проследить изменение значения функции на различных интервалах, т.е. при различных значениях аргумента.

В третьей задаче представлена работа с частным случаем многомерных массивов – матрицей. Использование матриц – весьма распространенное явление в программировании. Это, например, работа с преобразованием графики, моделирование трехмерных объектов. В математике матрицы также часто используются в различных задачах. Умение работать с ними – очень важно.

1. Вычисление значения интеграла функции,

заданной графически

Задания и постановка задачи.

Задание (вариант №15):

Составить программу на языке Turbo Pascal 7.0 вычисления значения интеграла на интервале [a, b] для функции, заданной графически. Значение интеграла вычислить приближённо по итерационной формуле левых прямоугольников:

I = ò f (x) dx @ I n = h (f 1 + f 2 +…+ f n-1),

где h=(b-a)/n – величина шага между двумя соседними точками разбиения интервала интегрирования; fi = f(xi) – значение функции в точке xi = a + h(i –1); i = 1, 2, …, n.

Вычисления закончить при выполнении условия |In – I2n| < e, где e>0 – достаточно малое значение, задаваемое пользователем (точность вычислений). Здесь In, I2n – значения интеграла, вычисленные по данной формуле при количестве разбиения на n и 2n соответственно.

Численные значения всех величин, участвующих в вычислениях, считать параметрами программы и определить их путём ввода.

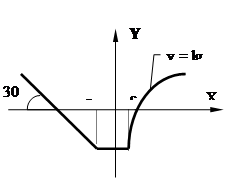График функции:

Пояснение к заданию:

Анализируя график функции можно сделать вывод, что для аналитического задания уравнения функции следует ее рассматривать на различных интервалах:

x <= -c Þ y = kx + b

-c < x < =c Þ y = Ln(c)

c < x Þ y = lg(x),

где kx + b =, lg x = (ln(x))/(ln(10));

x – аргумент функции; y – её значение; c – параметр функции (c>0), вводимые пользователем с клавиатуры.

1.2 Математическая формулировка задачи.

Решение многих задач (например, определение пути при неравномерном движении, работы переменной силы, расходов воды в реках и каналах, площади поперечного сечения судна) находится с помощью определённого интеграла. Иногда для вычисления определённого интеграла от непрерывной на отрезке [a; b] функции f (x) можно просто воспользоваться формулой Ньютона-Лейбница:

S = ò f(x) dx = F(b) – F(a),

где F (x) – первообразная для функции f (x) [ F ¢ (x)= f (x) ].

Однако воспользоваться формулой Ньютона-Лейбница в большинстве ситуаций не представляется возможным.

В этом случае используются приближённые методы для вычисления определённого интеграла. Все они основаны на том, что геометрически интеграл функции f (x) в пределах от a до b представляет собой площадь криволинейной трапеции, ограниченной графиком этой функции, осью Ox и прямыми x = a, x = b. Рассмотрим один из этих методов.

Численный метод решения.

Пусть требуется приближённо вычислить площадь фигуры, ограниченной графиком функции f (x) и прямыми x = a, x = b, y = 0.

Идея алгоритма вычисления площади криволинейной трапеции состоит в следующем:

Разобьем отрезок [a; b] на n равных отрезков точками a = x 0 < x 1 < x 2 <…< xn -1 < xn = b и на каждом из полученных отрезков построим прямоугольник, одной стороной которого будет отрезок [ xi, xi +1 ], а другой – отрезок, длина которого равна f (xi). Этот случай показан на рисунке 2.

Площадь криволинейной трапеции можно приближённо считать равной сумме площадей заштрихованных прямоугольников.

Ясно, что если увеличивать число отрезков [ xi, xi +1 ], т.е. отрезок

[a; b] разбивать на большее число равных отрезков, то сумма их площадей всё с большей точностью будет совпадать с площадью криволинейной трапеции. Значит, точность вычисления площади криволинейной трапеции определяется величиной числа n.

Площадь каждого прямоугольника можно вычислить так. Одна из сторон прямоугольника, построенного на отрезке [ xi, xi +1 ], равна h = (b - a) / n, а вторая – f (xi). Поэтому площадь «левого» прямоугольника равняется s = h * f (xi) = (b - a) / n * f (xi). Тогда площадь криволинейной трапеции равна сумме площадей всех прямоугольников:

S = (b - a)/n * f (x 0) + (b - a)/n * f (x 1) + … + (b - a)/n * f(xn-1) = (b - a)/n * (f(x0) + f(x1) +…+ f(xn-1)).

Таким образом, мы нашли интеграл функции f (x) на отрезке [ a; b ] при числе разбиений отрезка n. Очевидно, что чем больше n, тем больше точность вычисления значения интеграла; однако, при этом время, затрачиваемое на решение задачи, также прямо пропорционально числу n. Отсюда возникает вопрос: как правильно выбрать значение числа n, чтобы за наименьшее время найти значение искомого интеграла с предельно допустимой точностью?

Пусть мы знаем, что при разбиении отрезка интегрирования на n частей интеграл функции на данном интервале равен Integral1. Тогда мы можем также найти значение интеграла при числе разбиений отрезка, равном 2n, и это значение будет равняться некоторому числу Integral2. Очевидно, что оценкой точности вычислений будет являться величина абсолютной погрешности |Integral1 - Integral2|. Но в таком случае, именно величина абсолютной погрешности и есть тот критерий, который показывает, следует ли дальше продолжать вычисления или найденное значение интеграла уже удовлетворяет предельно допустимому уровню погрешности в поставленной задаче.

Тогда алгоритм решения задачи заключается в следующем:

Сначала вычисляется значение интеграла при n разбиений отрезка интегрирования (Integral1). Затем число разбиений n увеличивается в 2 раза и вычисляется значение интеграла при новом числе разбиений (Integral2). После этого проверяется условие завершения работы (|Integral1 - Integral2|<e) и, если работу следует продолжать, то текущее значение Integral2 присваивается значению Integral1, число разбиений n увеличивается в 2 раза, а значение Integral2 вычисляется заново и так далее, пока не будет выполнено условие |Integral1 - Integral2|<e.

Теперь нерешённым остался только вопрос о выборе начального значения числа n. Очевидно, что этот вопрос нельзя разрешить однозначно и одинаково для всех видов функций. Это станет очевидно, если рассмотреть следующую ситуацию: пусть требуется найти определённый интеграл некоторой функции на отрезке, где она принимает некоторое одинаковое значение не менее 2-х раз, и при этом её интеграл не равен произведению этого значения на длину отрезка интегрирования. При некорректном выборе исходного значения n может получиться так, что при разбиении отрезка интегрирования на n и 2n в рассмотрение будут приняты только те точки, значения функции в которых совпадают. Но тогда вычисление интеграла закончатся, т.к. разница между найденными значениями (Integral1 - Integral2) будет равна нулю и, следовательно, явно меньше любой погрешности, значение которой всегда положительно. Но это недопустимо, т.к. реальное значение искомого интеграла может быть далеко от найденного. Поэтому, при рассмотрении каждой новой функции следует производить тщательный анализ и исключение подобных ситуаций. Таким образом, вопрос о выборе начального значения числа разбиений отрезка остается открытым.

Так как рассматриваемая в данной задаче функция не представляет особой сложности, то в предложенном далее алгоритме решения задачи начальное значение числа n будет взято равным единице.

1.4 Описание переменных.

Имя переменной	Тип переменной	Значение
N	integer	Число интервалов разбиения
A	real	Нижний предел интегрирования
B	real	Верхний предел интегрирования
С	real	Параметр функции, определяемый пользователем
H	real	Шаг интегрирования
E	real	Точность вычислений
X	real	Аргумент функции
integral1	real	Значение интеграла при n разбиений
integral2	real	Значение интеграла при 2n разбиений

1.5 Схема алгоритма.

1.6 Текст программы.

PROGRAM KKP2_1_DUB3;

USES CRT;

var

A, B, C, E, ABS_Integral:real;

PROCEDURE ENTER_DATA(VAR PR_1, PR_2, P_PAR,POGR_PRO:REAL);

BEGIN

ClrScr;

Writeln ('Программа для нахождения значения интеграла на определенном промежутке');

Writeln;

writeln('Введите границы интервала [A,B],причем (A<B),число C (0<C<1) и точность E (E>0): ');

writeln;

REPEAT

BEGIN

writeln('Число C: '); readln(P_PAR);

if not (P_PAR>0) then

writeln ('C должно быть больше 0!. Повторите ввод.')

ELSE IF NOT (P_PAR<1) THEN

WRITELN('C должно быть меньше 1!. Повторите ввод.');

END;

UNTIL ((P_PAR>0) AND (P_PAR<1));

REPEAT

BEGIN

writeln('Начало интервала A: '); readln(PR_1);

writeln('Конец интервала B: '); readln(PR_2);

if not (PR_1<PR_2) then

writeln ('A должно быть меньше B!. Повторите ввод.');

END;

UNTIL (PR_1<PR_2);

REPEAT

BEGIN

writeln('Точность E: '); readln(POGR_PRO);

if not (POGR_PRO>0) then

writeln ('E должно быть больше 0!. Повторите ввод.');

END;

UNTIL (POGR_PRO>0);

END;

FUNCTION integration(VAR GR_1,GR_2,F_PAR,POGR_FUNC:REAL):real;

VAR

INTEGRAL1, INTEGRAL2, X, H:REAL;

N:INTEGER;

READY:BOOLEAN;

begin

integral1:=0;

integral2:=0;

n:=1;

REPEAT

N:=N*2;

H:=(GR_2-GR_1)/N;

X:=GR_1;

Integral2:=0;

repeat

if x<=(-F_PAR) then

integral2:=integral2+((1/sqr(3))*(ln(F_PAR)-F_PAR))

ELSE IF((-F_PAR<x) and (x<=F_PAR))

THEN integral2:=integral2+ln(F_PAR)

ELSE if (X>F_PAR) THEN

Integral2:=integral2+LN(X)/LN(10);

X:=X+H;

until not (X<=B);

READY:=abs(integral1-integral2)<POGR_FUNC;

INTEGRAL1:=INTEGRAL2;

UNTIL READY;

INTEGRATION:=INTEGRAL2;

END;

BEGIN

ENTER_DATA(A,B,C,E);

ABS_Integral:=INTEGRATION(A,B,C,E);

Writeln;

Writeln('Ответ: ');

writeln('Интеграл на промежутке от ',A:0:2,' до ',B:0:2,' равен ');

writeln (ABS_Integral:1:3,' с точностью ',E:1:3);

ReadKey;

END.

1.7 Инструкция пользователю.

Данная программа вычисляет значение интеграла функции заданной графически. Интервал интегрирования, точность вычислений и параметр функции вводятся пользователем. Программа вычислит результат и выдаст его (в числовом виде) на экран монитора.

После запуска программы на экране появится описание программы.

В ответ на приглашение к вводу значений следует ввести требуемые величины. Программа не претендует на универсальность, поэтому не стоит вводить запредельные границы интервала или очень маленькую (~0.001) точность вычислений. Поскольку скорость выполнения этой программы напрямую зависит от частоты процессора, то на процессорах, различающихся значительно, время вычислений (и допустимая точность) будут разными. В общем случае это определяется опытным путем.

Если все величины заданы корректно и вычисления не прерывались, то через некоторое время, зависящее от тактовой частоты процессора, программа подсчитает значение интеграла и выдаст его на экран.

В случае если требуется повторное вычисление значения, следует заново запустить программу.

1.8. Тестовый пример.

Программа для нахождения значения интеграла на определенном промежутке

Введите границы интервала [A,B], причем (A<B), число C (0<C<1), число D (D<0) и точность E (E>0):

Число C:

0.9

Число D:

-0.1

Начало интервала A:

Конец интервала B:

Точность E:

Ответ:

Интеграл на промежутке от A до B равен

2.574 с точностью 1.000

Программа для нахождения значения интеграла на определенном промежутке

Введите границы интервала [A,B], причем (A<B), число C (0<C<1), число D (D<0) и

точность E (E>0):

Число C:

0.9

Число D:

-0.1

Начало интервала A:

-0.9

Конец интервала B:

0.9

Точность E:

Ответ:

Интеграл на промежутке от A до B равен

-0.300 с точностью 1.000

2. Составление таблицы значений функции, заданной в виде разложения в ряд

Вариант задания и постановка задачи.

Задание (вариант №15):

Разработать алгоритм и составить программу вычисления таблицы значений функции, заданной в виде разложения в ряд. Значение функции вычислять с точностью e>0, т.е. вычисление суммы членов ряда необходимо прекратить, когда абсолютная величина очередного члена ряда разложения окажется меньше e: | а_к| <e.

При вычислении очередного члена целесообразно воспользоваться рекурентным выражением:

а_к+1=с_ка_к; к= 0, 1, 2,...,

где а_к - некоторый к-ый член ряда; а_к+1 - следующий к+1 -ый член ряда; с_к - коэффициент, определяемый номером к.

При составлении программы необходимо по возможности воспользоваться операторами организации циклов WHILE, REPEAT, FOR.

Границы интервала вычислений функций a и b, величина шага изменения аргумента h и точность вычисления функции e задаются при вводе. На печать выводятся номер по порядку, значение аргумента, соответствующие ему, значение функции и номер члена ряда, на котором закончилось вычисление значение функции, в форме таблицы:

№	Х	f (x)	№ _чл.р.
1
2
3
...

Функция:

2.2 Математическая формулировка задачи.

Некоторые функции нельзя представить в виде конечной формулы, но вычисление значений таких функций часто бывает необходимо для различного рода расчетов. Такие функции могут быть заданы в виде разложения в бесконечный ряд, где при бесконечном увеличении членов ряда каждый последующий член меньше предыдущего. Каждый член ряда – это конкретное значение функции. Нахождение таких членов и дает возможность вычислить значение функции. И чем больше членов ряда рассмотреть, тем более точным получится значение функции.

Численный метод решения.

Пусть требуется приближённо вычислить значение функции, заданной в виде разложения в бесконечный ряд. Идея алгоритма вычисления суммы членов ряда состоит в следующем:

Очевидно, что вычисление значения функции нужно производить за конечное число шагов. А значит, необходим некий ограничивающий фактор, в качестве которого в нашей задаче будет выступать погрешность вычислений e (e>0). Следовательно, вычислив каждый новый член ряда ak, нам необходимо проверить, не будет ли абсолютная величина очередного члена ряда меньше, чем величина погрешности e, т.е. | ak | < e. Если это неравенство не выполнилось, то следует вычислить новый член ряда, иначе можно заканчивать вычисление и выводить результат работы на экран дисплея.

Кроме того, при вычислении очередного члена целесообразно воспользоваться рекуррентным выражением: ak+1 = ck * ak; k = 0, 1, 2, …, где ak – некоторый k-ый член ряда; ak+1 - следующий k+1-ый член ряда; ck – коэффициент, определяемый номером k.

В данном случае нахождение коэффициента ck можно произвести следующим образом:

a_k= ;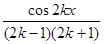

a_k₊₁= ;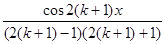

c_k =

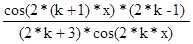
Следовательно, зная значение предыдущего члена ряда, порядковый номер следующего и используя полученную формулу, мы значительно упрощаем нахождение нового члена нашего ряда:

a_k₊₁ =a_k* 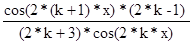; k = 0, 1, 2, …

2.4 Описание переменных.

Имя переменной	Тип переменной	Значение
K	integer	Номер члена ряда
number	integer	Порядковый номер
A	real	Начало интервала
B	real	Конец интервала
H		Шаг интервала
E		Точность
X		Текущее значение аргумента
у		Значение члена ряда
f		Значение функции для текущего аргумента

2.5 Схема алгоритма.

Программа предназначена для вычисления

таблицы значений функции,

заданной в виде разложения в ряд.

Введите границы интервала [A,B] (причем (A<B));

точность E (E>0)

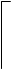и шаг изменения аргумента H (H>0)

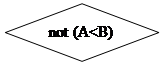ДА

НЕТ

ДА

нет

да

нет

да

нет

2.5.1 Схема алгоритма процедуры Table_begin

¦Номер¦ X ¦ f(x) ¦ Номер члена ряда ¦

2.5.2 Схема алгоритма процедуры Table_end

2.6 Текст программы.

Program kkr1_2;

procedure Table_begin;

begin

writeln(' ----------------------------------------------------------------------------------');

writeln(' ¦Номер¦ X ¦ f(x) ¦ Номер члена ряда ¦');

writeln(' ----------------------------------------------------------------------------------');

end;

procedure Table_end;

begin

writeln(' ----------------------------------------------------------------------------------');

end;

var

K,number:integer;

A,B,H,E,X,y,f:real;

begin

Writeln ('Программа предназначена для вычисления таблицы значений функции, ');

writeln ('заданной в виде разложения в ряд.');

Writeln;

{------------------------------------------------------------------------}

{Ввод данных}

writeln('Введите границы интервала [A,B] (причем (A<B)); точность E (E>0)');

writeln('и шаг изменения аргумента H (H>0)');

writeln;

repeat

begin

writeln('Начало интервала A: '); readln(A);

writeln('Конец интервала B: '); readln(B);

if not (A<B) then writeln ('A должно быть меньше B!. Повторите ввод.');

end;

until (A<B);

repeat

begin

writeln('Точность E: '); readln(E);

if not (E>0) then writeln ('E должно быть больше 0!. Повторите ввод.');

end;

until (E>0);

repeat

begin

writeln('Шаг H: ');readln(H);

if not (H>0) then writeln ('H должно быть больше 0!. Повторите ввод.');

end;

until (H>0);

{------------------------------------------------------------------------}

writeln('Вы ввели: ');

writeln('A=',A:1:5, ' B=',B:1:5,' H=',H:1:5,' E=',E:1:5);

writeln;

{------------------------------------------------------------------------}

X:=A;

number:=0;

Table_begin;

repeat

k:=0;

y:=(cos(2*x))/3;

f:=0;

inc(number);

repeat

inc(k);

y:=y*cos(2*(k+1)*x)*(2*k-1)/((2*k+3)*cos(2*k*x));

f:=f+y;

until (abs(y)<E);

if (number mod 18)=0 then

begin

Table_end;

Table_begin;

end;

writeln(' ¦',number:5,'¦', X:20:13,' ¦ ',(4/Pi)*(0.5-f):16:13, ' ¦ ',k:7,' ¦');

X:=X+H;

until not (X<B);

Table_end;

end.

2.7 Инструкция пользователю.

После запуска программы, она сообщит, что предназначена для составления таблицы значений функции на определенном интервале и попросит ввести значения, необходимые для составления таблицы. К таким значениям относятся начало и конец интервала, шаг изменения аргумента, точность вычислений. Не стоит вводить слишком больших значений (либо слишком маленькую точность), так как тогда время работы программы сильно увеличится.

Чтобы правильно составить требуемую таблицу, программе необходимы значения, которые пользователь введет в программу. Вводить значения надо после приглашения программы к соответствующему действию. Важный момент – если таблица полностью не поместиться на экран, то после заполнения последней строки, помещающейся на данном экране, программа попросит нажать любую клавишу и продолжить составление таблицы на чистом экране, т.е. предварительно очистив предыдущую таблицу.

2.8. Тестовый пример.

Программа предназначена для вычисления таблицы значений функции,

заданной в виде разложения в ряд.

Введите границы интервала [A,B] (причем (A<B)); точность E (E>0)

и шаг изменения аргумента H (H>0):

Начало интервала A:

0.5

Конец интервала B:

7.6

Точность E:

.001

Шаг H:

Вы ввели:

A=0.50000 B=7.60000 H=1.00000 E=0.00100

------------------------------------------------------------------------------------------

¦Номер¦ X ¦ f(x) ¦ Номер члена ряда ¦

------------------------------------------------------------------------------------------

¦ 1 ¦ 0.50000000000 ¦ 0.70477448832 ¦ 7 ¦

¦ 2 ¦ 1.50000000000 ¦ 0.57770993869 ¦ 8 ¦

¦ 3 ¦ 2.50000000000 ¦ 0.71713212380 ¦ 10 ¦

¦ 4 ¦ 3.50000000000 ¦ 0.66752823117 ¦ 10 ¦

¦ 5 ¦ 4.50000000000 ¦ 0.59106729937 ¦ 10 ¦

¦ 6 ¦ 5.50000000000 ¦ 0.72198206866 ¦ 2 ¦

¦ 7 ¦ 6.50000000000 ¦ 0.60541986599 ¦ 9 ¦

¦ 8 ¦ 7.50000000000 ¦ 0.61517755154 ¦ 10 ¦

------------------------------------------------------------------------------------------

3.Работа с матрицами

Вариант задания и постановка задачи.

Задание (вариант №15):

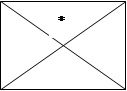
Вычислить сумму элементов матрицы В(К,К), К £ 50, расположенных над двумя диагоналями и под ними:

3.2 Математическая формулировка задачи.

12 Следующая ⇒

Воспользуйтесь поиском по сайту: