 |
Описание экспериментальной установки и метода исследования динамики движения катка по рельсовому пути
|
|
|
|
ФГОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА ФИЗИКИ
ЛАБОРАТОРНАЯ РАБОТА № 8
ИССЛЕДОВАНИЕ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ КАТКА ПО РЕЛЬСУ
Методическое указание к выполнению лабораторной работы по курсу общей
физики для студентов инженерно-технических специальностей
Калининград
ОГЛАВЛЕНИЕ
стр.
1. Введение 3
2. Описание экспериментальной установки и метода исследования динамики движения катка по рельсовому пути 3
3. Исследование энергетического баланса и определение К.П.Д. установки при движении катка 7
4. Порядок выполнения эксперимента и обработки результатов 8
5. Вопросы для проверки 11
6. Список литературы 11
Цель работы:
1. Ознакомление с физическими явлениями при качении твёрдых тел.
2. Изучение законов динамики, описывающих качение твёрдых тел.
3. Измерение момента инерции, момента сопротивления и коэффициента сопротивления качению.
4. Изучение энергетического баланса и измерение потерь энергии при качении.
Используемый реквизит: сменные грузы, ручной секундомер.
ВВЕДЕНИЕ
Катящиеся тела находят широкое применение в различных технических устройствах, особенно – на транспорте. Понимание физических явлений, обеспечивающих качение тел, и умение составить и решить систему уравнений, описывающих такое механическое движение, являются обязательными для каждого инженера-механика.
В большинстве практических приложений тела катятся по твёрдым опорным поверхностям, в частности, по рельсам. Однако в некоторых специальных устройствах типа грузоподъёмников (краны, полиспасты) вращающиеся блоки совершают качение по отвесным тросам или канатам.
|
|
|
Согласно принятой в механике классификации качение – это частный случай либо плоского (плоскопараллельного) движения, т.е. совокупности поступательного и вращательного движений, либо свободного движения как совокупности поступательного и сферического движений. Эти вопросы детально изучаются в курсе теоретической механики. В курсе общей физики обычно рассматривается только первый вид качения при плоском движении тел.
Особым условием, определяющим качение тел при плоском движении, является требование, чтобы в точках касания (контакта) между телом и опорной поверхностью происходило сцепление, обеспечивающее поворот тела относительно мгновенной, неподвижной оси, проходящей через эти точки.
Такие точки тела называются мгновенными центрами скоростей (м.ц.с.). При скатывании тел по отвесным тросам или канатам наличие м.ц.с. обеспечивается всегда. Однако при качении по твёрдым поверхностям возможно неполное сцепление в точках контакта: такое движение называется качением со скольжением. В отсутствие сцепления качение становится невозможным, при этом, например, колёса автомобиля вращаются «вхолостую» (буксуют). Качение тел при условии полного сцепления с опорной поверхностью называется нормальным качением. Кроме того, для нормального качения тело должно иметь радиально-симметричную форму и расположение центра масс на оси симметрии (для шара – в центре симметрии). При смещённом центре масс сила сцепления будет периодически изменяться, качение может происходить с отрывом («подскоком») на опорной поверхности.
В настоящей лабораторной работе требуется выполнить экспериментальное исследование нормального качения по рельсовому пути. Объектом исследования является каток, состоящий из сплошного цилиндра с закреплёнными на его торцах фигурными фланцами.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДА ИССЛЕДОВАНИЯ ДИНАМИКИ ДВИЖЕНИЯ КАТКА ПО РЕЛЬСОВОМУ ПУТИ
|
|
|
2.1. На рис.1 показан общий вид экспериментальной установки, включающей в себя рельсовый путь (2) и систему блоков (4, 5, 6). Горизонтальный и прямой рельсовый путь длиной L = 2,2 м изготовлен из стального швеллера с использованием двух его полок, по которым катится цилиндр катка (1). Для обеспечения устойчивого, нормального качения на поверхности цилиндра проточены две канавки, внутри которых происходит опора на рельсы.
Каток приводится в движение силой натяжения намотанной на него нити (3), на которой подвешен груз (8), опускающийся с начальной высоты h вместе с блоком (6). Блоки (5, 6) образуют полиспаст, уменьшающий высоту подъёма h в два раза по сравнению с длиной нити, намотанной на ободе цилиндра. Постоянная высота подъёма (и спуска) фиксирована двумя упорами: верхним (7) и нижним (9).
Примечание. В процессе наладки схемы для устранения скручивания нити и раскачивания груза вместо блока (6) установлено полукольцо с полированной канавкой, по которой скользит нить. При замене блока на полукольцо сохраняется принцип действия полиспаста и метод теоретического расчёта, приведенный в п. 2.2.
Рис. 1
Общий вид установки с катком
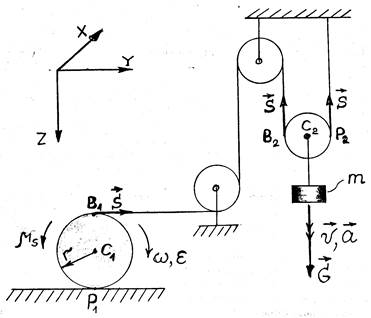
Рис. 2.
Расчётная схема установки.
2.2. На рис. 2 показана принципиальная расчётная схема установки. Здесь даны упрощённые изображения катка и системы блоков с грузом массой m. Показана система координат, на оси которой проектируются уравнения движения.
В т. В1 катка приложена сила натяжения нити 
. В т. Р1 расположен мгновенный центр скоростей, через который проходит (перпендикулярно плоскости рисунка) мгновенная ось вращения катка. В этой точке приложена сила сцепления, на схеме эта сила не обозначена, т.к. она не требуется для расчётов.
Изогнутая стрелка с обозначениями ω, ε условно показывает направление поворота при качении с сонаправленными векторами угловой скорости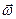 
и углового ускорения 
. В действительности векторы 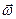и направлены вдоль оси х, имеют положительные проекции на данную ось. Положительную проекцию на ось х имеет вектор момента силы натяжения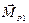 
, вычисляемый относительно м.ц.с. в т. Р1 и равный по модулю: 
, где 2 r – плечо силы , равное расстоянию от точки Р1 до точки В1.
|
|
|
Изогнутая стрелка с обозначением μS условно показывает, что при движении катка к нему приложена пара сил с моментом сопротивления качению, равным по модулю: 
, где: N – нормальная реакция, действующая со стороны рельсового пути; 
δ – плечо пары сил, равное расстоянию между линиями действия силы тяжести GK, приложенной к центру масс катка, и нормальной реакции N = GK. Смещение линии действия силы N объясняется деформацией поверхностей в точках контакта. Пара сил с моментом μS препятствует качению тела; вектор 
направлен противоположно вектору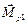 
.
Примечание. На схеме рис. 2 силы GK и N не показаны. Для более детального ознакомления с физическими явлениями при качении тел рекомендуется обратиться к специальным руководствам, приведенным в списке литературы. Имеется также описание в методических указаниях к лабораторной работе № 1 «Исследование качения стальных шаров».
Плечо пары δ называется коэффициентом сопротивления качению, в справочниках его величина дана в сантиметрах. При качении по стальным опорным поверхностям – для тел разной формы, изготовленных из стали,- величина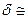 
(10-1 ÷ 10-3) см.
Для исследования нормального качения обычно применяется уравнение – закон динамики мгновенно-вращательного движения тел относительно оси, проходящей через м.ц.с. Векторная форма такого уравнения имеет вид:
(1)
Здесь: JP1 – момент инерции катка относительно мгновенной оси вращения; , , 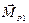- указанные выше векторы углового ускорения катка, момента силы натяжения относительно м.ц.с и момента сопротивления качению. Отметим, что момент силы сцепления, приложенной к катку в т. Р1, равен нулю, т.к. плечо этой силы оказывается равным нулю при расчёте относительно м.ц.с.
Примечание. Когда сцепление в точках контакта между катящимся телом и опорной поверхностью обеспечено, тогда величина силы сцепления несущественна. Это замечательное свойство сил сцепления имеет фундаментальное объяснение, состоящее в том, что мощность (и работа) сил сцепления равна нулю, т.к. такие силы приложены к м.ц.с. – точкам тела, имеющим нулевую скорость.
|
|
|
С помощью уравнения (1), как будет показано, можно найти неизвестный момент инерции катка JP1 и величину момента сопротивления μS. Для этого потребуется определить момент сил натяжения нити МР1 и угловое ускорение катка ε в зависимости от масс грузов, подвешиваемых на блоке в точке С2 (см. рис. 2).
Запишем уравнение поступательного движения груза массой m – II закон динамики Ньютона:
(2)
Здесь 
- ускорение груза, равное ускорению точки С2; 
- сила тяжести; - направленные вверх две силы натяжения нитей, скользящих по блоку с незначительным трением, которым пренебрегаем и по этой причине полагаем, что показанные на рис. 2 силы натяжения на двух участках нити равны между собой. Пренебрегая также массой двух других вспомогательных блоков и трением на их осях, получаем, что в т. В1 катка приложена такая же по величине сила натяжения нити, как и в т. В2 на блоке с грузом.
Величина силы S, необходимая для расчёта МР 1, определяется из уравнения (2), если известны ускорение груза 
и его масса. Масса груза дана в эксперименте; ускорение можно найти, измеряя время спуска t с заданной высоты h и учитывая, что при постоянных силах G и S выполняется известная из кинематики формула:
(3)
Осталось выяснить, как определяется угловое ускорение катка ε. Рассмотрим схему на рис. 2. При повороте катка полное (линейное) ускорение т. В1 равно векторной сумме центростремительного и вращательного ускорений. Вращательное ускорение направлено вдоль нити и равно:
(4)
С таким же по величине ускорением движутся все точки нити – вплоть до т. В2. Если такое условие нарушено, тогда скорости точек нити окажутся разными и нить должна разорваться (либо изменять длину при растяжении, но в данной схеме применяется нерастяжимая нить).
Итак, получили: 
. Теперь учтём, что (см. рис. 2) длина участка нити от точки Р2 до верхней точки закрепления нити увеличивается при опускании груза, но сама нить на этом участке остается неподвижной. Следовательно, в т. Р2 – мгновенный центр скоростей, относительно которого скорость и вращательное ускорение т. В2 в два раза больше, чем скорость и ускорение точки С2, где подвешен груз. В результате получаем:
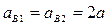(5)
где: - ускорение груза.
Из (4) и (5) имеем:
(6)
где: r – радиус катка.
Приведём теперь сводку формул, необходимых для обработки результатов опыта, записав уравнения движения катка и груза в виде проекций на оси координат.
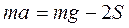(7а)
(7б)
(7в)
(7г)
Mp1 = 2rS (7д)
= at (7е)
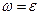t (7ж)
Здесь: t – время опускания груза массой m с высоты h; – линейная скорость груза в момент опускания на нижний упор с высоты h; ω – угловая скорость катка в конце пробега по рельсовому пути. Значения и ω понадобятся для исследования энергетического баланса и расчёта к.п.д. установки (эта тема рассмотрена в следующем разделе).
|
|
|
Отметим, что единственным видом прямых измерений в опыте является измерение времени опускания грузов. В эксперименте используются 5 грузов, для каждого из которых необходимо измерить время спуска с высоты h не менее пяти раз. Значения масс грузов, высоты спуска и радиуса катка также являются результатом прямых измерений, но эти данные получены заранее и приведены в разделе «Порядок выполнения эксперимента». В этом же разделе будет дана методика определения момента инерции катка и момента сопротивления качению – с помощью графика, построенного для уравнения (7б), которое получено из векторного уравнения (1).
|
|
|
