 |
Функция. Схема иерархии функций задачи.
|
|
|
|
Лабораторная работа 3.
Использование функций
Задание. На основании индивидуального задания для каждой из двух задач разработать иерархию функций, описать назначение и таблицу спецификаций для каждой функции, составить алгоритмы каждой функции, программу на языке C#, таблицы тестов, программы и оттестировать их для задач по указанию преподавателя.
Индивидуальные задания
Задачи А
1. Описать функцию Power(A, st), вычисляющую заданную степень st числа A. С помощью этой функции найти вторую, третью и четвертую степень пяти данных чисел.
2. Описать функцию Mean(X, Y), вычисляющую среднее геометрическое Gmean = X Y двух положительных чисел X и Y. С помощью этой функции найти среднее геометрическое для пар (A, B), (A, C), (A, D), если даны A, B, C, D.
3. Описать функцию RectPS(x 1, y 1, x 2, y 2), вычисляющую площадь S прямоугольника со сторонами, параллельными осям координат, по координатам (x 1, y 1), (x 2, y 2) его противоположных вершин. С помощью этой функции найти площади трех прямоугольников с данными противоположными вершинами.
4. Описать функцию DigitCountSum(K), находящую сумму цифр целого положительного числа K. С помощью этой функции найти сумму цифр для каждого из пяти данных целых чисел.
5. Описать функцию InvertDigits(K), меняющую порядок следования цифр целого положительного числа K на обратный. С помощью этой функции поменять порядок следования цифр на обратный для каждого из пяти данных целых чисел.
6. Описать функцию Swap(X, Y), вычисляющую сумму параметров. С ее помощью для данных переменных A, B, C, D последовательно сложить содержимое следующих пар: A и B, C и D, B и C.
7. Описать функцию Minmax(X, Y,Z), определяющую минимальное или максимальное из значений X и Y в зависимости от значения Z. Используя четыре вызова этой функции, найти минимальное и максимальное из данных чисел A, B, C, D.
|
|
|
8. Описать функцию SortInc(A, B, C,D), меняющую содержимое переменных A, B, C таким образом, чтобы их значения оказались упорядоченными либо по возрастанию, либо по убыванию в зависимости от значения D. С помощью этой функции упорядочить по возрастанию два данных набора из трех чисел: (A 1, B 1, C 1) и (A 2, B 2, C 2).
9. Описать функцию Sign(X) целого типа, возвращающую для вещественного числа X следующие значения: –1, если X < 0; 0, если X = 0; 1, если X > 0. С помощью этой функции найти значение выражения Sign(A) + Sign(B) для данных вещественных чисел A и B.
10. Описать функцию CircleSR вещественного типа, находящую площадь круга радиуса R (R — вещественное). С помощью этой функции найти площади трех кругов с данными радиусами. Площадь круга радиуса R вычисляется по формуле S = р· R 2.
11. Описать функцию RingS(R 1, R 2) вещественного типа, находящую площадь кольца, заключенного между двумя окружностями с общим центром и радиусами R 1 и R 2 (R 1 и R 2 — вещественные, R 1 > R 2). С ее помощью найти площади трех колец, для которых даны внешние и внутренние радиусы.Воспользоваться формулой площади круга радиуса R: S = р· R 2.
12. Описать функцию TriangleP(a, h), находящую периметр равнобедренного треугольника по его основанию a и высоте h, проведенной к основанию (a и h — вещественные). С помощью этой функции найти периметры трех треугольников, для которых даны основания и высоты. Для нахождения боковой стороны b треугольника использовать теорему Пифагора:
b 2 = (a /2)2 + h 2.
13. Описать функцию SumRange(A, B) целого типа, находящую сумму всех целых чисел от A до B включительно (A и B — целые). Если A > B, то функция возвращает 0. С помощью этой функции найти суммы чисел от A до B и от B до C, если даны числа A, B, C.
14. Описать функцию Calc(A, B, Op) вещественного типа, выполняющую над ненулевыми вещественными числами A и B одну из арифметических операций и возвращающую ее результат. Вид операции определяется целым параметром Op: 1 — вычитание, 2 — умножение, 3 — деление, остальные значения — сложение. С помощью Calc выполнить для данных A и B операции, определяемые данными целыми N 1, N 2, N 3.
|
|
|
15. Описать функцию Quarter(x, y) целого типа, определяющую номер координатной четверти, в которой находится точка с ненулевыми вещественными координатами (x, y). С помощью этой функции найти номера координатных четвертей для трех точек с данными ненулевыми координатами.
16. Описать функцию Even(K) логического типа, возвращающую True, если целый параметр K является четным, и False в противном случае. С ее помощью найти количество четных чисел в наборе из 10 целых чисел.
17. Описать функцию IsSquare(K) логического типа, возвращающую True, если целый параметр K (> 0) является квадратом некоторого целого числа, и False в противном случае. С ее помощью найти количество квадратов в наборе из 10 целых положительных чисел.
18. Описать функцию IsPowerN(K, N) логического типа, возвращающую True, если целый параметр K (> 0) является степенью числа N (> 1), и False в противном случае. Дано число N (> 1) и набор из 10 целых положительных чисел. С помощью функции IsPowerN найти количество степеней числа N в данном наборе.
19. Описать функцию DigitCount(K) целого типа, находящую количество цифр целого положительного числа K. Используя эту функцию, найти количество цифр для каждого из пяти данных целых положительных чисел.
20. Описать функцию IsPalindrom(K), возвращающую True, если целый
параметр K (> 0) является палиндромом (то есть его запись читается одинаково слева направо и справа налево), и False в противном случае. С ее помощью найти количество палиндромов в наборе из 10 целых положительных чисел.
21. Описать функцию Fact(N) вещественного типа, вычисляющую значение факториала N! = 1·2·…· N (N > 0 — параметр целого типа; вещественное возвращаемое значение используется для того, чтобы избежать целочисленного переполнения при больших значениях N). С помощью этой функции найти факториалы пяти данных целых чисел.
22. Описать функцию Fact2(N) вещественного типа, вычисляющую двойной факториал:
N!! = 1·3·5·…· N, если N — нечетное;
N!! = 2·4·6·…· N, если N — четное
(N > 0 — параметр целого типа; вещественное возвращаемое значение используется для того, чтобы избежать целочисленного переполнения при больших значениях N). С помощью этой функции найти двойные факториалы пяти данных целых чисел.
|
|
|
23. Описать функцию Power2(A, N) вещественного типа, находящую величину AN (A — вещественный, N — целый параметр) по следующим формулам:
A 0 = 1; AN = A · A ·…· A (N сомножителей), если N > 0;
AN = 1/(A · A ·…· A) (| N | сомножителей), если N < 0.
С помощью этой функции найти AK, AL, AM, если даны числа A, K, L, M.
24. Описать функцию NOD2(A, B) целого типа, находящую наибольший общий делитель (НОД) двух целых положительных чисел A и B, используя алгоритм Евклида:
НОД(A, B) = НОД(B, A mod B), если B > 0; НОД(A, 0) = A.
С помощью этой функции найти наибольшие общие делители пар (A, B), (A, C), (A, D), если даны числа A, B, C, D.
25. Описать функцию TimeToHMS(T, H, M, S), определяющую по времени T (в секундах) содержащееся в нем количество часов H, минут M и секунд S. Используя эту функцию, найти количество часов, минут и секунд для пяти данных отрезков времени T 1, T 2, …, T 5.
26. Описать функцию IncTime(H, M, S, T), которая увеличивает на T секунд время, заданное в часах H, минутах M и секундах S. Дано время (в часах H, минутах M, секундах S) и целое число T. Используя функцию IncTime, увеличить данное время на T секунд и вывести новые значения H, M, S.
27. Описать функцию IsLeapYear(Y) логического типа, которая возвращает True, если год Y является високосным, и False в противном случае. Вывести значение функции IsLeapYear для пяти данных значений параметра Y. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400.
Задачи В
В каждом задании предполагается, что заданы две целые квадратные матрицы С и Т порядка n 2<=n<=10
1. Пусть сумма элементов обеих диагоналей матрицы С равна S1, а сумма элементов обеих диагоналей матрицы T равна S2. Если S1 <S2, то найти матрицу Н=А+S1Т, иначе матрицу Z=B+S2(C+T). Здесь A- матрица порядка n, все элементы которой равны S1; B- матрица порядка n, все элементы которой равны S2.
2. Найти k1-количество элементов ниже побочной диагонали матрицы C, меньших a, и k2-количество элементов ниже побочной диагонали матрицы Т, меньших b. Если k1<k2, найти F=T+2k1C, иначе найти H=2C-k2T.
|
|
|
3. Найти a – сумму элементов матрицы T, лежащих на и выше главной диагонали, и b- элементов матрицы C, лежащих на и выше главной диагонали. Если a>b, определить H=T-abC; иначе определить F=C+aT.
4. Найти n – количество чётных чисел на главной и побочной диагонали матрицы T и m – количество чётных чисел на главной и побочной диагонали матрицы C.Если n<m, найти H=Tt+n*C, иначе найти F=Ct+m*T,где Tt,Ct – транспонированные матрицы T и C, соответственно.
5. Найти k – количество нечетных чисел ниже побочной диагонали матрицы T и m – количество нечетных чисел матрицы C.Если k>m, найти H=(1/m)*T+C, иначе найти F=k*(C+T)+T.
6. Найти k1-количество чисел, меньших 7 в некоторой заданной строке матицы T, k2-количество чисел, меньших 12 в некоторой заданной строке матрицы C. Если k1<k2, найти S=T+(k1+k2)*C, иначе найти F=k1*T+k2*C.
7. Найти k1 – количество чисел на главной диагонали матрицы C, не равных a, и k2- количество чисел на главной диагонали матрицы T, не равных b. Если k1≠k2, найти F=C+T, иначе найти H=Ct+Tt, где Ct, Tt-транспонированные матрицы для C и T, соответственно.
8. Если количество равных элементов в первых двух строках матрицы C больше количества равных чисел в последних двух строках матицы T, то найти H=T*C+2*C, иначе найти F=3*T-C*T.
9. Если количество отрицательных элементов ниже главной диагонали матрицы C больше количества отрицательных элементов ниже главной диагонали матрицы T, то найти F=C*T-Tt, иначе найти H=Ct-T*C,где Tt, Ct – транспонированные матрицы для T и C, соответственно.
10. Пусть a – количество элементов столбца с заданным номером p матрицы C, больших соответствующих элементов столбца с номером f матрицы T; b –количество элементов столбца с номером f матрицы C, больших соответствующих элементов столбца p матрицы Т. Если a>b, то найти матрицу Z=aT+b(C+T), иначе найти H=T+(a-b)C.
11. Если сумма четных элементов побочной диагонали матрицы C больше суммы четных элементов побочной диагонали матрицы T, то найти H=T+2C, иначе найти F=C-5T.
12. Дополнительно заданы два целых числа l и m. Если l<m, то получить матрицу A=lT+mC и подсчитать количество положительных элементов в l-ом столбце матрицы T; иначе получить матрицу B=12t+m2C и подсчитать количество положительных элементов в m-ом столбце матрицы C.
13. Дополнительно заданы два целых числа m и k. Получить матрицы B=T-k*C, D=C+m*T и найти в столбце с номером m матрицы B номер элемент, который будет первым по порядку больше 1, найти аналогичный элемент в k-ом столбце матрицы D.
14. Получить два вектора C1 и T1 по следующему правилу: складываются все элементы 1-го столбца исходной матрицы – эта сумма будет первым элементом получаемого вектора и т. П.
|
|
|
Получив вектор C1, указать номер элемента, который первый по порядку будет кратен 5; аналогично – для T1.
15. Найти k1 – количество положительных чисел, кратных 5, выше главной диагонали матрицы T и k2- количество положительных чисел, кратных 3, выше главной диагонали матрицы C. Если k1>k2,найти F=T*C+3*C, иначе найти H=5*T+C*T.
16. Дополнительно заданы два целых числа m и n. Если в строке с номером m матрицы C есть отрицательные элементы, а в строке с номером n матрицы T есть положительные элементы, то найти A=-C+T*C,иначе найти B=-T+C*T.
17. Если S- сумма элементов последней строки и последнего столбца матицы T больше P- суммы элементов последней строки и последнего столбца матрицы C, то найти F=C+2Tt, иначе найти H=T+5Ct.,где Tt,Сt- транспонированные матрицы для T и C, соответственно.
18. Найти a – количество элементов k-ой строки матрицы T, меньших соответствующих элементов l-ой строки матрицы C; найти b – количество элементов l-ой строки матрицы T, меньших соответствующих элементов k-ой строки матрицы C. Если a>b, то найти H=a*T+b*C, иначе найти F=b*T+a*C.
19. Дополнительно заданы два целых числа k и m. Найти n – количество не равных k элементов матрицы C, и l-количество не равных m элементов матрицы T. Если n>l, то найти H=Tt*C+k*T, иначе найти F=Ct*T+l*C, где Tt, Ct- транспонированные матрицы для T и C, соответственно.
20. Пусть p – сумма элементов двух заданных строк матрицы T, а q – сумма элементов двух других заданных строк матрицы C. Если p=q, то найти D=2*T-p*C,иначе найти H=p*T=q*C.
21. Если количество нечетных элементов на обеих диагоналях матрицы T больше количества нечетных элементов в матрице C, то найти D=E+T+C, иначе найти H=2*E+T+3*C, где E- единичная матрица вида
1 0 0 0
E= 0 1 0 0
0 0 1 0
0 0 0 1
22. Если произведение элементов побочной диагонали матрицы T меньше произведения элементов побочной диагонали матрицы C, то найти H=T-3*C+E, иначе найти F=C+2*T+2*E, где E- единичная матрица вида
1 0 0 0
E= 0 1 0 0
0 0 1 0
0 0 0 1
23. Дополнительно заданы номера строк P,Q. Пусть SP – количество случаев, когда соответствующие элементы строк с номером P одновременно четны в C и T,а SQ – количество случаев, когда соответствующие элементы строк с номером Q одновременно четны в C и T. Если SP=SQ, то получить A=SP(C+T)+SQ E, иначе получить B=SQ(C+E)+SP T. Здесь E- единичная матрица
1 0 0 0
E= 0 1 0 0
0 0 1 0
0 0 0 1
24. Найти S- сумму элементов в последней строке матрицы C. Если все элементы матрицы C больше соответствующих элементов матрицы T, то найти P-сумму элементов в первой строке матрицы T и матрицу A=(S+P)C-T, иначе найти матрицу B=nC+SnT.
Функция. Схема иерархии функций задачи.
Довольно часто необходимо, чтобы некоторые подзадачи, например, поиск максимального значения в массиве, выполнялись в нескольких точках программы. Конечно, можно добавлять в приложение идентичные (или почти идентичные) разделы кода всякий раз, когда в этом возникает необходимость, но такой подход имеет свои недостатки. Изменение даже одной небольшой детали алгоритма в таком случае означает, что соответствующие изменения потребуется вносить во множество разделов кода, которые могут быть разбросаны по всему приложению. Пропуск одного из этих разделов может повлечь за собой серьезные последствия и сделать неработоспособным все приложение. К тому же это еще и существенно удлиняет приложение.
Решить эту проблему позволяют функции.
Функции в языке С# являются средствами предоставления блоков кода, которые могут выполняться в любой точке приложения.
Например, можно создать функцию, вычисляющую максимальное значение в массиве. Далее ее можно выполнять из любой точки в коде и в каждом случае использовать для этого одинаковые строки кода. Поскольку описывать этот код нужно только один раз, любые вносимые в него изменения будут отражаться на данной операции вычисления при всяком ее применении. Функции также могут применяться для создания универсального кода, что позволяет им выполнять одни и те же операции над варьирующимися данными. Предоставлять необходимую для работы информацию функциям можно в виде параметров, а получать от них результаты — в виде возвращаемых значений. В предыдущем примере в роли параметра мог бы выступать подлежащий поиску массив, а в роли возвращаемого значения — максимальная величина в этом массиве. Это означает, что одну и ту же функцию можно было бы использовать для работы каждый раз с другим массивом.
При решении любой, достаточно сложной задачи, как уже говорилось ранее, первым этапом является внешнее проектирование – разбиение задачи на подзадачи и составление таблицы спецификаций для каждой подзадачи.
Разбиение задачи на подзадачи оформляется в виде схемы иерархии, причем подзадачи выделяются по общности выполняемых ими действий. К одной и той же подзадаче, реализуемой в виде функции, может происходить обращение несколько раз с различными параметрами. Важно только, чтобы эти параметры всегда передавались в одном и том же порядке, соответствующем их перечислению в заголовке функции.
Пример разбиения задачи на подзадачи:
Заданы две матрицы целых чисел A(m,m) и B(k,k) и два вектора из целых чисел X(m) и Y(k), где 1<m£10 1<k£8. Вычисляются P – число нулевых элементов на главной диагонали матрицы A и Q – число нулевых элементов на главной диагонали матрицы B. Если P<Q, то необходимо получить вектор C(m), а в противном случае - вектор D(k), где 


 i=1..m
i=1..m  i=1..k
i=1..k
Проведя анализ задачи, можно построить следующую схему иерархии подзадач данной задачи (Рис.):
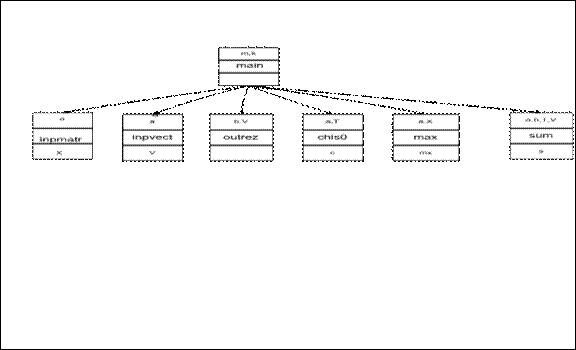
Рис. 3. Схема иерархии подзадач примера
Каждая подзадача изображается прямоугольником, поделенным на 3 части. В средней части указывается имя функции, в верхней части перечисляются имена входных параметров, в нижней – возвращаемые значения.
Здесь main - главная функция, выполняющая решение всей задачи;
inpmatr - функция ввода матрицы;
inpvect - функция ввода вектора;
chis0 - функция подсчета числа нулевых элементов на главной диагонали матрицы;
sum - функция вычисления суммы произведений строки матрицы на вектор;
outrez - функция вывода результирующего вектора;
max - функция нахождения максимального элемента матрицы.
Для каждой функции составим таблицу спецификаций и словесный алгоритм
|
|
|


