Дифракция Фраунгофера на одной щели

Дифракция Фраунгофера (или дифракция плоских световых волн, или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию.

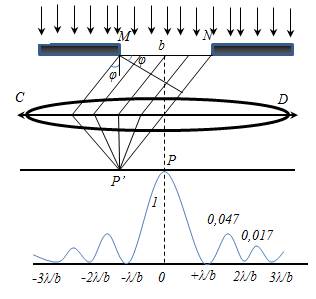Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели (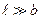), 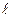- длина, b - ширина. Разность хода между лучами 1 и 2 в направ­лении φ

Разобьём волновую поверхность на участке щели МN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уложится 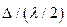зон. Т.к. свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Число зон Френеля 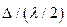укладывающихся на ширине щели, зависит от угла φ.

Условие минимума при дифракции Френеля:

Если число зон Френеля четное

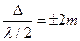
или

то в т. Р наблюдается дифракционный минимум.

Условие максимума:

Если число зон Френеля нечетное

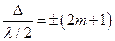
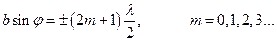
то наблюдается дифракционный максимум.

При φ’=0, Δ = 0 в щели укладывается одна зона Френеля и, следо­вательно, в т. Р главный (центральный) максимум нулевого порядка.

Основная часть световой энергии сосредоточена в главном максимуме: m =0:1:2:3...; I =1: 0,047: 0,017: 0,0083... (m -порядок максимума; I - интенсивность).

Сужение щели приводит к уширению главного максимума и уменьшению его яркости (то же и с другими максимумами). При уширении щели (b>λ) максимумы будут ярче, но дифракционные полосы становятся уже, а числе самих полос - больше. При b>> λ центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.

При падении белого света будет разложение на его составляющие. При этом фиолетовый свет будет отклоняться меньше, синий - больше и т.д., красный - максимально. Главный максимум в этой случае будет белого цвета.

 

 

Вопрос

Дифракционная решётка — оптический прибор, действие которого основано на использовании явлениядифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.

Виды решёток[

· Отражательные: Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отражённом свете

· Прозрачные: Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете.

Описание явления[

Так выглядит свет лампы накаливанияфонарика, прошедший через прозрачную дифракционную решётку. Нулевой максимум (m =0) соответствует свету, прошедшему сквозь решётку без отклонений. В силу дисперсии решётки в первом (m =±1) максимуме можно наблюдать разложение света в спектр. Угол отклонения возрастает с ростом длины волны (от фиолетового цвета к красному)

Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр.

Формулы[править | править вики-текст]

Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.

Если известно число штрихов ({\displaystyle N}N), приходящихся на 1 мм решётки, то период решётки находят по формуле: d=1/N{\displaystyle d=1/N} мм.

Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:

{\displaystyle d\,\sin \alpha =k\lambda }d sin a =ky

где

{\displaystyle d}d — период решётки,

{\displaystyle \alpha }a — угол максимума данного цвета,

{\displaystyle k}k — порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,

{\displaystyle \lambda }y — длина волны.

Если же свет падает на решётку под углом {\displaystyle \theta }0, то:

{\displaystyle d\ \{\sin \alpha -\sin \theta \}=k\lambda } d { sin a-sin 0}=ky

 

 

Вопрос

И поляризованный свет

Следствием теории Максвелла (см. § 162) является поперечность световых волн: век­торы напряженностей электрического Е и магнитного Н полей волны взаимно пер­пендикулярны и колеблются перпендику­лярно вектору скоростиv распространения волны (перпендикулярно лучу). Поэтому для описания закономерностей поляри­зации света достаточно знать поведение лишь одного из векторов. Обычно все рассуждения ведутся относительно све­тового вектора — вектора напряженно­сти Е электрического поля (это название обусловлено тем, что при действии света на вещество основное значение имеет электрическая составляющая поля волны, действующая на электроны в атомах ве­щества).

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы же излучают световые во­лны независимо друг от друга, поэтому световая волна, излучаемая телом в це­лом, характеризуется всевозможными рав­новероятными колебаниями светового век­тора (рис. 272, а; луч перпендикулярен плоскости рисунка). В данном случае рав­номерное распределение векторов Е объясняется большим числом атомарных

излучателей, а равенство амплитудных значений векторов Е — одинаковой (в среднем) интенсивностью излучения каждого из атомов. Свет со всевозможны­ми равновероятными ориентациями векто­ра Е (и, следовательно, Н) называется естественным.

Свет, в котором направления колеба­ний светового вектора каким-то образом упорядочены, называется поляризован­ным. Так, если в результате каких-либо внешних воздействий появляется преиму­щественное (но не исключительное!) на­правление колебаний вектора Е (рис. 272, б), то имеем дело с частично поляризованным светом. Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендику­лярном лучу (рис. 272, в), называется плоскополяризованным (линейно поляри­зованным).

Плоскость, проходящая через направ­ление колебаний светового вектора плос­кополяризованной волны и направление распространения этой волны, называ­ется плоскостью поляризации. Плоскопо­ляризованный свет является предельным случаем эллиптически поляризованного света — света, для которого вектор Е (вектор Н /2 и равенстве амплитуд склады­ваемых волн), то имеем дело сp=±j), то имеем дело с рассмотренным выше плоскополяризо­ванным светом, если в окружность (приp, равной нулю илиj) изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпендикулярной лучу. Если эллипс поляризации вырождается (см. § 145) в прямую (при разности фаз циркулярно поляризованным (поляризованным по кру­гу) светом.

Степенью поляризации называется личина

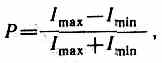
где I_maxиI_min — максимальная и мини­мальная интенсивности света, соответ­ствующие двум взаимно перпендикуляр­ным компонентам вектора Е. Для естественного светаI_max=I_min и Р=0, для плоскополяризованногоI_min=0 и Р =1.

Естественный свет можно преобразо­вать в плоскополяризованный, используя так называемые поляризаторы, пропуска­ющие колебания только определенного на­правления (например, пропускающие ко­лебания, параллельные плоскости поляри­затора, и полностью задерживающие колебания, перпендикулярные этой плоскости). В качестве поляризаторов мо­гут быть использованы среды, анизотроп­ные в отношении колебаний вектора Е, например кристаллы (их анизотропия из­вестна, см. § 70). Из природных кристал­лов, давно используемых в качестве поля­ризатора, следует отметить турмалин.

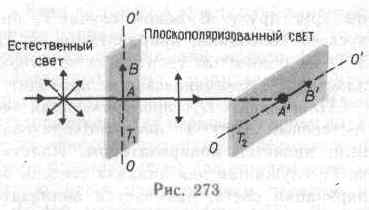
Рассмотрим классические опыты с турмалином (рис.273). Направим естест­венный свет перпендикулярно пластинке турмалина T₁, вырезанной параллельно так называемой оптической оси ОО (см. §192). Вращая кристалл T₁ вокруг направления луча, никаких изменений ин­тенсивности прошедшего через турмалин света не наблюдаем. Если на пути луча поставить вторую пластинку турмалина Т₂ и вращать ее вокруг направления луча, то интенсивность света, прошедшего через пластинки, меняется в зависимости от уг­ла а между оптическими осями кристал­лов по закону Малюса:

I=I₀cos², (190.1)a

где I ₀и I — соответственно интенсивности света, падающего на второй кристалл и вышедшего из него. Следовательно, ин­тенсивность прошедшего через пластинки света изменяется от минимума (полное

=0 (оптические оси пласти­нок параллельны). Однако, как это следу­ет из рис. 274, амплитудаa/2 (оптические оси пластинок перпендикулярны) до мак­симума приp=aгашение света) при Е световых коле­баний, прошедших через пластинку Т₂, будет меньше амплитуды световых колеба­ний Е ₀, падающих на пластинкуT₂:

E=E₀.acos

Так как интенсивность света пропорцио­нальна квадрату амплитуды, то и получа­ется выражение (190.1).

Результаты опытов с кристаллами тур­малина объясняются довольно просто, ес­ли исходить из изложенных выше условий пропускания света поляризатором. Пер­вая пластинка турмалина пропускает ко­лебания только определенного направле­ния (на рис. 273 это направление показано стрелкой АВ) т. е. преобразует естествен­ный свет в плоскополяризованный. Вторая же пластинка турмалина в зависимости от ее ориентации из поляризованного света пропускает большую или меньшую его часть, которая соответствует компонен­ту Е, параллельному оси второго турмали­на. На рис. 273 обе пластинки расположе­ны так, что направления пропускаемых ими колебаний АВ и А'В' перпендикуляр-

ны друг другу. В данном случае T₁ про­пускает колебания, направленные по АВ, а Т₂их полностью гасит, т. е. за вторую пластинку турмалина свет не проходит.

Пластинка t₁, преобразующая ес­тественный свет в плоскополяризрванный, является поляризатором. Пластин­ка Т₂, служащая для анализа степени по­ляризации света, называется анализато­ром. Обе пластинки совершенно одинако­вы (их можно поменять местами).

Если пропустить естественный свет че­рез два поляризатора, плоскости которых образуют угол а, то из первого выйдет плоскополяризованный свет, интенсив­ность которого I₀=¹/₂I_ест, из второго, согласно (190.1), выйдет свет интенсивно­стьюI =I₀ocos². Следовательно, ин­тенсивность света, прошедшего через два поляризатора,a

I=¹/₂I_естcos², откудаIa_max=¹/₂I_ecт (поляризаторы параллельны) иI_min=0 (поляризаторы скрещены).

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: