базовый уровень, время – 1 мин)

Тема: Системы счисления и двоичное представление информации в памяти компьютера.

Что нужно знать:

· перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной системами счисления (см. презентацию «Системы счисления»)

Полезно помнить, что в двоичной системе: · четные числа оканчиваются на 0, нечетные – на 1; · числа, которые делятся на 4, оканчиваются на 00, и т.д.; числа, которые делятся на 2k, оканчиваются на k нулей · если число N принадлежит интервалу 2k-1 £ N < 2k, в его двоичной записи будет всего k цифр, например, для числа 125:                           26 = 64 £ 125 < 128 = 27, 125 = 11111012 (7 цифр) · числа вида 2k записываются в двоичной системе как единица и k нулей, например:      16 = 24 = 100002 · числа вида 2k-1 записываются в двоичной системе k единиц, например:      15 = 24-1 = 11112 · если известна двоичная запись числа N, то двоичную запись числа 2·N можно легко получить, приписав в конец ноль, например: 15 = 11112,     30 = 111102,         60 = 1111002, 120 = 11110002

· желательно выучить наизусть таблицу двоичного представления чисел 0-7 в виде триад (групп из 3-х битов):

X 10, X 8	X­2		X 10, X 8	X­2
0	000		4	100
1	001		5	101
2	010		6	110
3	011		7	111

и таблицу двоичного представления чисел 0-15 (в шестнадцатеричной системе – 0-F₁₆) в виде тетрад (групп из 4-х битов):

X 10	X­2		X 10	X­16	X­2
0	0000		8	8	1 000
1	0001		9	9	1 001
2	0010		10	A	1 010
3	0011		11	B	1 011
4	0100		12	C	1 100
5	0101		13	D	1 101
6	0110		14	E	1 110
7	0111		15	F	1 111

· отрицательные целые числа хранятся в памяти в двоичном дополнительном коде (подробнее см. презентацию «Компьютер изнутри»)

· для перевода отрицательного числа (- a) в двоичный дополнительный код нужно сделать следующие операции:

o перевести число a-1 в двоичную систему счисления;

o сделать инверсию битов: заменить все нули на единицы и единицы на нули в пределах разрядной сетки (см. пример Р-00 далее).

Пример задания:

Р-06. Сколько единиц в двоичной записи восьмеричного числа 1731₈?

Решение:

1) для решения достаточно знать двоичные коды чисел от 1 до 7, поскольку для перевода восьмеричного числа в двоичную систему можно достаточно каждую цифру отдельно записать в виде тройки двоичных (триады):

2) 1731₈ = 001 111 011 001₂

3) в этой записи 7 единиц

4) Ответ: 7

Ещё пример задания:

Р-05. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 5 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

Решение:

5) вообще, минимальное двоичное число, содержащее 5 единиц – это 11111₂, но в восьмеричной системе оно записывается как 37 – двухзначное число

6) минимальное четырёхзначное восьмеричное число – 1000₈ = 1 000 000 000₂, для решения задачи в конце этого числа нужно заменить четыре нуля на единицы:

1 000 001 111₂  = 1017₈

7) Ответ: 1017

Ещё пример задания:

Р-04. Сколько единиц в двоичной записи десятичного числа 519?

Решение:

8) проще всего представить заданное число в виде суммы степеней числа 2:

519 = 512 + 7 = 2⁹ + 4 + 3 = 2⁹ + 2² + 2 + 1 = 2⁹ + 2² + 2¹ + 2⁰

9) количество единиц в двоичной записи числа равно количеству слагаемых в таком разложении

10) Ответ: 4

Ещё пример задания:

Р-03. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 6 единиц. Если таких чисел несколько, укажите наибольшее из них.

1) 63₁₀ * 4₁₀   2) F8₁₆ + 1₁₀   3) 333₈            4) 11100111₂

Решение:

11) нужно перевести все заданные числа в двоичную систему, подсчитать число единиц и выбрать наибольшее из чисел, в которых ровно 6 единиц;

12) для первого варианта переведем оба сомножителя в двоичную систему:

63­₁₀ = 111111­₂              4₁₀ = 100­₂

в первом числе ровно 6 единиц, умножение на второе добавляет в конец два нуля:

63­₁₀ * 4₁₀ = 111111­₂ * 100­₂ = 111111­00₂

то есть в этом числе 6 единиц

13) для второго варианта воспользуемся связью между шестнадцатеричной и двоичной системами счисления: каждую цифру шестнадцатеричного числа можно переводить отдельно в тетраду (4 двоичных цифры):

F­₁₆ = 1111­₂     8₁₆ = 100­0₂     F8₁₆ = 1111 1000₂

после добавления единицы F8₁₆ + 1 = 1111 1001₂ также получаем число, содержащее ровно 6 единиц, но оно меньше, чем число в первом варианте ответа

14) для третьего варианта используем связь между восьмеричной и двоичной системами: каждую цифру восьмеричного числа переводим отдельно в триаду (группу из трёх) двоичных цифр:

333₈ = 011 011 011­₂ = 11011011₂

это число тоже содержит 6 единиц, но меньше, чем число в первом варианте ответа

15) последнее число 11100111₂ уже записано в двоичной системе, оно тоже содержит ровно 6 единиц, но меньше первого числа

16) таким образом, все 4 числа, указанные в вариантах ответов содержат ровно 6 единиц, но наибольшее из них – первое

17) Ответ: 1.

Ещё пример задания:

Р-02. Сколько единиц в двоичной записи числа 1025?

1) 1       2) 2  3) 10 4) 11

Решение (вариант 1, прямой перевод):

18) переводим число 1025 в двоичную систему: 1025 = 10000000001­₂

19) считаем единицы, их две

20) Ответ: 2

Возможные проблемы: легко запутаться при переводе больших чисел.

Решение (вариант 2, разложение на сумму степеней двойки):

1) тут очень полезно знать наизусть таблицу степеней двойки, где 1024 = 2¹⁰ и 1 = 2⁰

2) таким образом, 1025= 1024 + 1 = 2¹⁰ + 2⁰

3) вспоминая, как переводится число из двоичной системы в десятичную (значение каждой цифры умножается на 2 в степени, равной её разряду), понимаем, что в двоичной записи числа ровно столько единиц, сколько в приведенной сумме различных степеней двойки, то есть, 2

4) Ответ: 2

Возможные проблемы: нужно помнить таблицу степеней двойки.

Когда удобно использовать: · когда число чуть больше какой-то степени двойки

Ещё пример задания:

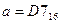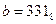Р-01. Дано: и . Какое из чисел с, записанных в двоичной системе счисления, удовлетворяет  неравенству a < c < b?    

1) 11011001₂       2)  11011100₂          3)  11010111₂     4) 11011000₂

Общий подход:

перевести все числа (и исходные данные, и ответы) в одну (любую!) систему счисления и сравнить.

Решение (вариант 1, через десятичную систему):

5)

6)

7) переводим в десятичную систему все ответы:

11011001₂ = 217,  11011100 ₂= 220,         11010111₂ = 215,         11011000₂=216

8) очевидно, что между числами 215 и 217 может быть только 216

9) таким образом, верный ответ – 4.

Возможные проблемы: арифметические ошибки при переводе из других систем в десятичную.

Решение (вариант 2, через двоичную систему):

1)  (каждая цифра шестнадцатеричной системы отдельно переводится в четыре двоичных – тетраду);

2) 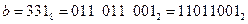 (каждая цифра восьмеричной системы отдельно переводится в три двоичных – триаду, старшие нули можно не писать);

3) теперь нужно сообразить, что между этими числами находится только двоичное число 11011000₂ – это ответ 4.

 

Возможные проблемы: запись двоичных чисел однородна, содержит много одинаковых символов – нулей и единиц, поэтому легко запутаться и сделать ошибку.

Решение (вариант 3, через восьмеричную систему):

1) (сначала перевели в двоичную систему, потом двоичную запись числа разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, так как для чисел от 0 до 7 их восьмеричная запись совпадает с десятичной);

2) 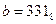, никуда переводить не нужно;

3) переводим в восьмеричную систему все ответы:

11011001₂ = 011 011 001₂ = 331₈ (разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, как в п. 1)          

11011100 ₂= 334₈, 11010111₂ = 327₈,       11011000₂=330₈

4) в восьмеричной системе между числами 327₈ и 331₈ может быть только 330₈

5) таким образом, верный ответ – 4.

 

Возможные проблемы: нужно помнить двоичную запись чисел от 0 до 7 (или переводить эти числа в двоичную систему при решении).

Решение (вариант 4, через шестнадцатеричную систему):

1) 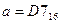 никуда переводить не нужно;

2)   (сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F);

3) переводим в шестнадцатеричную систему все ответы:

11011001₂ = 1101 1001₂ = D9₁₆ (разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F, как в п. 1)    

11011100 ₂= DC₁₆, 11010111₂ = D7₁₆,       11011000₂=D8₁₆

4) в шестнадцатеричной системе между числами D7₁₆ и D9₁₆ может быть только D8₁₆

5) таким образом, верный ответ – 4.

Возможные проблемы: нужно помнить двоичную запись чисел от 0 до 15 (или переводить эти числа в двоичную систему при решении).

Выводы:

· есть несколько способов решения, «каждый выбирает для себя»;

· наиболее сложные вычисления – при переводе всех чисел в десятичную систему, можно легко ошибиться;

· сравнивать числа в двоичной системе сложно, также легко ошибиться;

· видимо, в этой задаче наиболее простой вариант – использовать восьмеричную систему, нужно просто запомнить двоичные записи чисел от 0 до 7 и аккуратно все сделать;

· в других задачах может быть так, что выгоднее переводить все в десятичную или шестнадцатеричную систему счисления.

Еще пример задания:

Р-00. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-78)?

1) 3       2) 4      3) 5        4) 6

Решение (вариант 1, классический):

1) переводим число 78 в двоичную систему счисления:

78 = 64 + 8 + 4 + 2 = 2⁶ + 2³ + 2² + 2¹ = 1001110₂

2) по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов

3) чтобы получилось всего 8 разрядов (бит), добавляем впереди один ноль:

78 = 01001110₂

4) делаем инверсию битов (заменяем везде 0 на 1 и 1 на 0):

01001110₂ → 10110001₂ 

5) добавляем к результату единицу

10110001₂ + 1 = 10110010₂

это и есть число (-78) в двоичном дополнительно коде

6) в записи этого числа 4 единицы

7) таким образом, верный ответ – 2.

Возможные ловушки и проблемы: · нужно не забыть в конце добавить единицу, причем это может быть не так тривиально, если будут переносы в следующий разряд – тут тоже есть шанс ошибиться из-за невнимательности

Решение (вариант 2, неклассический):

1) переводим число 78 – 1=77 в двоичную систему счисления:

77 = 64 + 8 + 4 + 1 = 2⁶ + 2³ + 2² + 2⁰ = 1001101₂

2) по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов

3) чтобы получилось всего 8 разрядов (бит), добавляем впереди один ноль:

77 = 01001101₂

4) делаем инверсию битов (заменяем везде 0 на 1 и 1 на 0):

01001101₂ → 10110010₂ 

это и есть число (-78) в двоичном дополнительно коде

5) в записи этого числа 4 единицы

6) таким образом, верный ответ – 2.

Возможные ловушки и проблемы: · нужно помнить, что в этом способе в двоичную систему переводится не число a, а число a-1; именно этот прием позволяет избежать добавления единицы в конце (легче вычесть в десятичной системе, чем добавить в двоичной)

Решение (вариант 3, неклассический):

1) переводим число 78 в двоичную систему счисления:

78 = 64 + 8 + 4 + 2 = 2⁶ + 2³ + 2² + 2¹ = 1001110₂

2) по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов

3) чтобы получилось всего 8 разрядов (бит), добавляем впереди один ноль:

78 = 01001110₂

4) для всех битов, которые стоят слева от младшей единицы, делаем инверсию битов (заменяем везде 0 на 1 и 1 на 0):

01001110₂ → 10110010₂ 

это и есть число (-78) в двоичном дополнительно коде

5) в записи этого числа 4 единицы

6) таким образом, верный ответ – 2.

Возможные ловушки и проблемы: · нужно помнить, что при инверсии младшая единица и все нули после нее не меняются

Задачи для тренировки [1]:

1) Как представлено число 83₁₀ в двоичной системе счисления?

1) 1001011₂ 2) 1100101₂                3) 1010011₂      4) 101001₂

2) Сколько единиц в двоичной записи числа 195?

3) Сколько единиц в двоичной записи числа 173?

4) Как представлено число 25 в двоичной системе счисления?

1) 1001₂            2) 11001₂           3) 10011₂           4) 11010₂

5) Как представлено число 82 в двоичной системе счисления?

1) 1010010₂ 2) 1010011₂                3) 100101₂        4) 1000100₂

6) Как представлено число 263 в восьмеричной системе счисления?

1) 301₈               2) 650₈                3) 407₈            4) 777₈

7) Как записывается число 567₈ в двоичной системе счисления?

1) 1011101₂ 2) 100110111₂           3) 101110111₂ 4) 11110111₂

8) Как записывается число A87₁₆ в восьмеричной системе счисления?

1) 435₈         2) 1577₈              3) 5207₈             4) 6400₈

9) Как записывается число 754₈ в шестнадцатеричной системе счисления?

1) 738₁₆        2) 1A4₁₆              3) 1EC₁₆             4) A56₁₆

10) Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-128)?

11) Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-35)?

12) Дано: 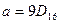, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 10011010₂       2) 10011110₂      3) 10011111₂        4) 11011110₂

13) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11111001₂       2) 11011000₂      3) 11110111₂        4) 11111000₂

14) Дано: 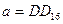, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11011010₂       2) 11111110₂      3) 11011110₂        4) 11011111₂

15) Дано: , 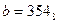. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11101010₂       2) 11101110₂      3) 11101011₂        4) 11101100₂

16) Дано: 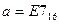, 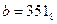. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11101010₂       2) 11101000₂      3) 11101011₂        4) 11101100₂

17) Дано: 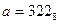, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11010011₂       2) 11001110₂      3) 11001010₂        4) 11001100₂

18) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11100011₂       2) 11011010₂      3) 10101101₂        4) 11011101₂

19) Сколько единиц в двоичной записи числа 64?

20) Сколько единиц в двоичной записи числа 127?

21) Сколько значащих нулей в двоичной записи числа 48?

22) Сколько значащих нулей в двоичной записи числа 254?

23) Какое из чисел является наименьшим?

1) E6₁₆          2) 347₈               3) 11100101₂  4) 232

24) Какое из чисел является наибольшим?

1) 9B₁₆          2) 234₈               3) 10011010₂  4) 153

25) Дано: 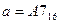, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 10101100₂       2) 10101010₂      3) 10101011₂        4) 10101000₂

26) Дано: 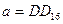, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11011010₂       2) 11111110₂      3) 11011111₂        4) 11011110₂

27) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 10001010₂       2) 10001110₂      3) 10010011₂        4) 10001100₂

28) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 11101010₂       2) 11101110₂      3) 11101100₂        4) 11101011₂

29) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 10101010₂       2) 10111100₂      3) 10100011₂        4) 10101100₂

30) Сколько единиц в двоичной записи числа 173?

31) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 1000000₂       2) 1000110₂          3) 1000101₂           4) 1000111₂

32) Дано: 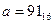, . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 10001001₂       2) 10001100₂      3) 11010111₂        4) 11111000₂

33) Дано: , . Какое из чисел С, записанных в шестнадцатеричной системе счисления, удовлетворяет неравенству ?

1) AA₁₆           2) B8₁₆                   3) D6₁₆              4) F0₁₆

34) Дано: , . Какое из чисел Z, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 111111001₂       2) 111100111₂      3) 110111100₂      4) 110110111₂

35) Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?

1) 10111010₂       2) 10101010₂      3) 101010100₂        4) 10100010₂

36) Сколько единиц в двоичной записи десятичного числа 513?

37) Сколько значащих нулей в двоичной записи десятичного числа 497?

38) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит ровно 3 единицы.

1) 1                2) 11           3) 3             4) 33

39) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит ровно 2 единицы.

1) 7                2) 11           3) 12          4) 15

40) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит ровно 4 единицы.

1) 15             2) 21           3) 32          4) 35

41) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит ровно 2 единицы.

1) 14             2) 16           3) 18          4) 31

42) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит ровно 3 единицы.

1) 8                2) 10           3) 12          4) 14

43) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит наибольшее количество единиц.

1) 13             2) 14           3) 15          4) 16

44) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит наибольшее количество единиц.

1) 23             2) 24           3) 25          4) 26

45) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит наибольшее количество значащих нулей.

1) 3                2) 8             3) 11          4) 15

46) Для каждого из перечисленных ниже десятичных чисел построили двоичную запись. Укажите число, двоичная запись которого содержит наибольшее количество значащих нулей.

1) 13             2) 18           3) 21          4) 25

47) Даны 4 целых числа, записанные в двоичной системе:
              10001011, 10111000, 10011011, 10110100.
Сколько среди них чисел, больших, чем А4₁₆ +20₈?

 

48) Даны 4 целых числа, записанные в двоичной системе:
              10101011, 11001100, 11000111, 11110100.
Сколько среди них чисел, меньших, чем BC₁₆ +20₈?

 

49) Даны 4 целых числа, записанные в двоичной системе:
              11000000, 11000011, 11011001, 11011111.
Сколько среди них чисел, больших, чем AB₁₆ +25₈?

 

50) Даны 4 целых числа, записанные в двоичной системе:
              10111010, 10110100, 10101111, 10101100.
Сколько среди них чисел, меньших, чем 9C₁₆ +37₈?

 

51) Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если таких чисел несколько, укажите наибольшее из них.

1) 31₁₀ * 8₁₀ + 1₁₀         2) F0₁₆ + 1₁₀   3) 351₈            4) 11100011₂

 

52) Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 4 единицы. Если таких чисел несколько, укажите наибольшее из них.

1) 15₁₀ * 16₁₀ + 4₁₀      2) D7₁₆ + 1₁₀   3) 344₈            4) 11100001₂

 

53) (http://ege.yandex.ru) Сколько единиц в троичной записи десятичного числа 243?

54)  (http://ege.yandex.ru) Сколько единиц в троичной записи десятичного числа 242?

55)  (http://ege.yandex.ru) Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если таких чисел несколько, укажите наибольшее из них.

1) 15₁₀            2) 77₈            3) 345₈            4) FA₁₆

56) Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 6 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

57) Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит ровно 3 нуля. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

58) Укажите набольшее четырёхзначное восьмеричное число, двоичная запись которого содержит 4 единицы. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

59) Укажите наибольшее четырёхзначное восьмеричное число, двоичная запись которого содержит ровно 4 нуля. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

60) Укажите наименьшее число, двоичная запись которого содержит ровно три значащих нуля и две единицы. Ответ запишите в десятичной системе счисления.

61) Укажите набольшее число, двоичная запись которого содержит ровно три значащих нуля и две единицы. Ответ запишите в десятичной системе счисления.

62) Сколько единиц в двоичной записи десятичного числа 245?

63) Сколько единиц в двоичной записи десятичного числа 501?

64) Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 5 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

65) Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 7 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

66) Укажите наибольшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 6 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

67) Укажите наибольшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 9 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

68) Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 6 значащих нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

69) Укажите наибольшее число, двоичная запись которого содержит ровно три значащих нуля и две единицы, причём единицы не стоят рядом. Ответ запишите в десятичной системе счисления.

70) Сколько единиц в двоичной записи восьмеричного числа 6543₈?

71) Сколько единиц в двоичной записи восьмеричного числа 1234₈?

72) Сколько единиц в двоичной записи восьмеричного числа 6123₈?

73) Сколько значащих нулей в двоичной записи восьмеричного числа 7512₈?

74) Сколько значащих нулей в двоичной записи восьмеричного числа 1253₈?

75) Сколько значащих нулей в двоичной записи восьмеричного числа 7715₈?

76) Сколько единиц в двоичной записи шестнадцатеричного числа 4FA7₁₆?

77) Сколько единиц в двоичной записи шестнадцатеричного числа 1234₁₆?

78) Сколько единиц в двоичной записи шестнадцатеричного числа 6AB1₁₆?

79) Сколько значащих нулей в двоичной записи шестнадцатеричного числа 75BD₁₆?

80) Сколько значащих нулей в двоичной записи шестнадцатеричного числа 1253₁₆?

81) Сколько значащих нулей в двоичной записи шестнадцатеричного числа 3FC5₁₆?

82) Вычислите: 10101010₂ – 252₈ + 7₁₆. Ответ запишите в десятичной системе счисления.

83) Вычислите: 10101011₂ – 253₈ + 6₁₆. Ответ запишите в десятичной системе счисления.

84) Определите количество натуральных чисел, удовлетворяющих неравенству: 11001011₂ < x < CF₁₆.

85) Определите количество натуральных чисел, удовлетворяющих неравенству: 11000111₂ < x < CD₁₆.

86) Определите количество натуральных чисел, удовлетворяющих неравенству: 11000011₂ < x < CA₁₆.

87) Определите количество натуральных чисел, удовлетворяющих неравенству: 11010010₂ < x < DA₁₆.

88) Определите количество натуральных чисел, удовлетворяющих неравенству: 11010111₂ < x < DB₁₆.

89) Определите количество натуральных чисел, удовлетворяющих неравенству: 11010110₂ < x < DC₁₆.

90) Определите количество натуральных чисел, удовлетворяющих неравенству: 11010011₂ < x < DF₁₆.

91) Определите количество натуральных чисел, удовлетворяющих неравенству: 11001110₂ < x < DE₁₆.

92) Определите количество натуральных чисел, удовлетворяющих неравенству: 11110000₂ < x < FA₁₆.

93) Определите количество натуральных чисел, удовлетворяющих неравенству: 11100101₂ < x < FC₁₆.

94) (Д.В. Богданов) Определите количество натуральных чисел, удовлетворяющих неравенству:
EEA₁₆ < x < 7640₈.

95) (А.Н. Носкин) Определите количество натуральных чисел, удовлетворяющих неравенству:

(170₈ + FE₁₆) ≤ x ≤ (200₈ + 11111111₂).

96) (А.Н. Носкин) Определите количество натуральных чисел, удовлетворяющих неравенству:

(96₁₆ + 18₁₆) < x < (240₈ + 33₈).

97) (А.Н. Носкин) Определите количество натуральных чисел, удовлетворяющих неравенству:

(D2₁₆ - 28₁₆) < x ≤ (346₈ - 50₈).

98) (А.Н. Носкин) Определите количество натуральных чисел, удовлетворяющих неравенству:

(64₁₆ - 1E₁₆) ≤ x ≤ (50₈ + 36₈).

99) Определите количество натуральных чисел, удовлетворяющих неравенству:

AA₁₆  ≤ x < 411₈.

100) Определите количество натуральных чисел, удовлетворяющих неравенству:

BB₁₆  < x ≤ 523₈.

101) Определите количество натуральных чисел, удовлетворяющих неравенству:

AB₁₆  < x < 344₈.

102) Определите количество натуральных чисел, удовлетворяющих неравенству:

312₈  < x < CD₁₆.

103) Определите количество натуральных чисел, удовлетворяющих неравенству:

213₈  ≤ x ≤ AD₁₆.

 

 

[1] Источники заданий:

1. Демонстрационные варианты ЕГЭ 2004-2016 гг.

2. Тренировочные и диагностические работы МИОО.

3. Гусева И.Ю. ЕГЭ. Информатика: раздаточный материал тренировочных тестов. — СПб: Тригон, 2009.

4. Якушкин П.А., Лещинер В.Р., Кириенко Д.П. ЕГЭ 2010. Информатика. Типовые тестовые задания. — М.: Экзамен, 2010.

5. Абрамян М.Э., Михалкович С.С., Русанова Я.М., Чердынцева М.И. Информатика. ЕГЭ шаг за шагом. — М.: НИИ школьных технологий, 2010.

6. Чуркина Т.Е. ЕГЭ 2011. Информатика. Тематические тренировочные задания. — М.: Эксмо, 2010.

7. Самылкина Н.Н., Островская Е.М. ЕГЭ 2011. Информатика. Тематические тренировочные задания. — М.: Эксмо, 2010.

8. Крылов С.С., Ушаков Д.М. ЕГЭ 2015. Информатика. Тематические тестовые задания. — М.: Экзамен, 2015.

9. Ушаков Д.М. ЕГЭ-2015. Информатика. 20 типовых вариантов экзаменационных работ для подготовки к ЕГЭ. — М.: Астрель, 2014.

Поделиться:

Воспользуйтесь поиском по сайту: