Перед союзом и запятая не ставится, если части сложносочиненного предложения объединены каким-либо общим элементом.

Рис.1. Общая схема регулируемого АД с изменением параметров напряжения обмотки статора

 

2.2.3.1. Изменение напряжения, приложенного к двигателю при постоянной частоте питающего напряжения

Данный способ также основан на изменении скольжения АД.

Его мы также рассмотрели в прошлом семестре и отмечали свойственные этому способу недостатки: малый диапазон регулирования, уменьшение перегрузочной способности, большие потери.

В связи с особенностями регулирования данный способ управления АД применяется для решения ограниченного числа задач, например, следующих:

- обеспечение плавного пуска/торможения АД за счет ограничения пускового/тормозного момента и токов;

- экономия энергии при недогрузках [40];

- регулирование скорости в насосных и вентиляторных установках, то есть в механизмах, у которых момент сопротивления при снижении угловой скорости резко снижается. Тем самым становится возможным регулировать скорость АД в области допустимых потерь энергии. Это позволяет создать простую и относительно недорогую систему регулируемого электропривода насосов и вентиляторов [30].

 

2.2.3.2. Частотное управление

В отличие от векторного управления АД, частотное управление можно назвать скалярным. В [45] оно названо модульным управлением, поскольку, в отличие от векторного управления, оно базируется на изменении модулей величин, определяющих электромагнитный момент АД (частоты, напряжения, токов и магнитных потоков).

Этот способ управления заключается в изменении как частоты, так и амплитуды питающего напряжения.

Этот способ управления координатами является эффективным для ЭП с короткозамкнутым асинхронным двигателем.

Способ управления, при котором регулируется частота и напряжение, называют частотным управлением, а способ, при котором регулируется частота и ток, называют частотно-токовым управлением [13].

В состав ЭП с частотным управлением входит преобразователь частоты.

Электропривод, который в качестве преобразовательного устройства использует преобразователь частоты, называется частотно-регулируемым электроприводом [19].

На вход ПЧ подается стандартное напряжение сети U ₁ (например, линейное трехфазное напряжение 380 В) промышленной частоты f ₁=50Гц, а с выхода снимается переменное напряжение U _1рег регулируемой частоты f _рег.

Достоинства

По сравнению с параметрическими способами управления

1) Плавное регулирование угловой скорости АД в достаточно широком диапазоне (от нуля до номинальной и выше).

2) Экономичность. Регулирование скорости и работа АД в переходных режимах происходит без больших потерь мощности в роторной цепи и относительно малых потерях в вентильных преобразователях частоты [11].

3) Плавный разгон и торможение

По сравнению с векторным управлением

4) Техническая простота измерения и регулирования переменных [13].

5) Возможность построения разомкнутых систем регулирования скоростью [13].

Недостатки

По сравнению с векторным управлением

1) Относительно низкое быстродействие. Трудность реализации желаемых законов изменения скорости и момента в динамических режимах [13].

2) Относительно малый диапазон регулирования угловой скорости (до 1:20); до 1:40 [20].

3) Отсутствие возможности точной регулировки скорости вращения вала, так как она зависит от нагрузки [23].

4) Частотный регулятор не позволяет контролировать момент на валу двигателя [23].

По сравнению со способом, связанным с изменением только напряжения

5) Преобразователь частоты более дорогое устройство, чем преобразователь напряжения.

Область применения

Скалярное управление является наиболее распространенным и применяется в приводах насосов, компрессоров, вентиляторов и других механизмов, в которых необходимо поддержание технологического параметра: давления в трубопроводе или другого [15].

Для этих областей качеств, свойственных частотному управлению, достаточно, поэтому классические структуры частотного управления нашли широкое распространение [16].

Экономические выгоды частотного регулирования особенно существенны для электроприводов, работающих в повторно-кратковременном режиме, где имеет место частое изменение направления вращения с интенсивным торможением [36].

 

2.2.3.3. Векторное управление.

При векторном регулировании, в отличие от частотного, управление скоростью осуществляется с помощью регулирования амплитуды вектора потокосцепления двигателя Y и его фазы.

Потокосцепление - физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки, и численно равная сумме магнитных потоков, проходящих через каждый виток катушки: Y =Ф w.

Смысл векторного управления состоит в том, что система управления отслеживает напряжение на обмотках, ток двигателя и сдвиг фаз между ними, создает математические модели двигателя, рассчитывает скольжение и положение ротора. На основании этих данных в каждый момент времени рассчитывается оптимальное положение магнитного поля (вектора Y) и генерируются соответствующие выходные сигналы [18].

Перед союзом и запятая не ставится, если части сложносочиненного предложения объединены каким-либо общим элементом.

Достоинства:

- широкий диапазон регулирования (до 1:10000) [16],

- высокое быстродействие [16].

Векторное управление позволяет работать с полным моментом в области нулевых частот, точно поддерживать скорость при переменной нагрузке без датчика обратной связи, точно контролировать момент на валу двигателя [18].

Недостатки:

- сложность управляющих и функциональных устройств для получения широкого диапазона регулирования скорости.

Область применения:

- приводы станков, роботов и т.п. [16], т.е. там, где в наибольшей степени востребованы перечисленные достоинства этого способа управления

В рамках Раздела 2 будут рассмотрены структуры АД при частотном (скалярном) управлении. Векторное управление будет рассмотрено в Разделе 3.

 

2.3. Законы частотного управления асинхронным электроприводом

Законом частотного управления АД будем называть зависимость величины напряжения U ₁, подаваемого на обмотку статора, от частоты напряжения f ₁, реализуемую при управлении АД с целью изменения его частоты вращения.

 

2.3.1. Запись параметров управления в относительной форме

В теории частотного управления широко используется запись параметров управления в относительной форме. При этом используются следующие обозначения:

Частота в относительной форме: α = f ₁/ f _1ном=ω₀/ω_0ном

Напряжение в относительной форме: γ = U ₁/ U _1ном

Частота ротора в относительной форме (она же – абсолютное скольжение): β = f ₂/ f _2ном=ω₂/ω_0ном= (ω₀- ω)/ω_0ном.

Собственно скольжение s=(ω₀–ω)/ω₀, записываемое в относительной форме, в теории частотного регулирования не используется, так как при изменяющейся ω₀ оно не дает четкого представления о характере протекающих процессов.

 

2.3.2. Базовый закон регулирования угловой скорости АД при частотном управлении

Основными критериями эффективности способа управления ЭП являются:

1) плавное регулирование скорости в широком диапазоне;

2) эффективная работа в установившихся режимах при любой угловой скорости в пределах этого диапазона, в частности в отношении КПД;

3) оптимальная работа в переходных режимах при пуске и при изменении скорости вращения, в частности, в отношении быстродействия;

4) надежность и устойчивость работы ЭП;

5) экономичность.

Если они присущи рассматриваемому способу управления – то они записываются в достоинства, если отсутствуют – в недостатки.

При управлении АД его работа в любой момент времени (включая переходный процесс) характеризуется положением точки на определенной механической характеристике. Положение этой механической характеристики соответствует текущему значению частоты и амплитуды напряжения (а также ряду других параметров, которые мы при частотном управлении не изменяем).

Какими же должны быть механические характеристики, чтобы названные требования выполнялись?

Они должны:

а) Обладать высокой жесткостью рабочего участка.

При этом скольжение АД (и пропорциональные ему потери) будет минимальным, а КПД работы АД высоким. Кроме того, высока будет стабильность угловой скорости при изменении момента сопротивления (нагрузки).

б) При любой скорости вращения должна обеспечиваться заданная перегрузочная способность М _макс/ М _с.ном = const.

Для обеспечения требований а) и б) одного изменения только частоты, или только напряжения недостаточно. Требуется одновременное изменение обоих параметров по определенному закону, называемому законом частотного управления.

Впервые этот закон вывел и разработал метод регулирования в целом советский электротехник Михаил Костенко в 1925 году [1]. Назовем выведенный им закон базовым.

При выводе базового закона частотного управления были приняты следующие допущения:

1) Магнитная цепь двигателя не насыщена (индуктивные сопротивления пропорциональны частоте f: x_L =w L =2π fGw ². Когда магнитная цепь не насыщена магнитная проводимость G =const.

2) Активное сопротивление обмотки статора пренебрежимо мало (по сравнению с индуктивным сопротивлением) и принимается равным нулю: R ₁=0.

Отметим следующее. При частоте f ₁=50 Гц индуктивное сопротивление (контура намагничивания) на порядок (для машин малой мощности) или на два порядка (для машин большой мощности) больше, чем активное сопротивление R ₁. Поэтому при анализе и расчете АД, работающих при постоянной номинальной частоте питающего напряжения, такое допущение используют часто [46]. А при частотном регулировании угловой скорости АД предполагается, что частота напряжения будет меняться в широких пределах. В п.2.3.5 будет показано, что это допущение в ряде случаев становится грубым.

3) Ток в стержнях обмотки ротора распределяется равномерно [7] (то есть R ₂ не зависит от частоты тока ротора).

4) Условия охлаждения не зависят от частоты вращения двигателя [7]. Следовательно, это не влияет на температуру элементов двигателя и сопротивления R ₁ и R ₂.

Выражение для максимального (критического) момента выглядит следующим образом (см. Раздел 3 ЭПЛА):

(2)

С учетом принятых допущений выражение (2) может быть преобразовано к виду:

(3)

Входящие в (3) параметры можно записать через частоту напряжения

х 1 + х '2= w*(L s1 + L s2') = k 1 f

(4)

 

W0 = k 2 f

(5)

В итоге

М макс = k 3 * (U / f)2

(6)

Таким образом, для сохранения перегрузочной способности двигателя при данном способе регулирования необходимо, чтобы для угловых скоростей W и W_ном 

k 3 (U 1/ f 1)2 / М с = k 3 (U 1ном/ f 1ном)2/ М с.ном

(7)

где М _с, М _с.ном – моменты нагрузки, соответствующие угловым скоростям W и W_ном. Определяются по статической характеристике нагрузки М _с (W).

Путем несложных преобразований получаем, что для того, чтобы обеспечить при всех значениях скорости W и нагрузки М _с оптимальный режим работы АД, необходимо при регулировании с изменением частоты напряжения питания f ₁ изменять также и уровень напряжения U ₁ на зажимах двигателя по закону:

(8)

Частные виды законов регулирования при частотном управлении определяются исходя из аналитического выражения статической характеристики нагрузки М _с(W).

Примеры:

1) При моменте нагрузки М _с=const, закон изменения напряжения и частоты при регулировании выглядит так:

U 1/ U 1ном= f 1/ f 1ном  или   U 1/ f 1=const

(9)

2) Нагрузка характеризуемая постоянством мощности P =const

С учетом (1), пренебрегая изменением скольжения при изменении момента:

P = M cW~ M c 2π f 1/ p = kM c f 1

(10)

Из формулы (10) следует

M c= P /(kf)

(11)

После подстановки (11) в (8) получим закон регулирования при P =const

или

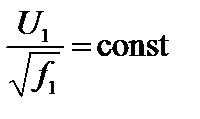
(12)

3) Вентиляторная нагрузка М _с= k W²

После перехода (аналогично п.2) от угловой скорости к частоте напряжения получим приближенно: М _с= kf ²

После подстановки в (8) получим закон регулирования для вентиляторной нагрузки

(13)

Семейство механических характеристик при реализации указанных законов регулирования приведено на рис.2.

Рис.2. Механические характеристики АД при реализации законов частотного регулирования

а) Мс= const; б) P = const; в) вентиляторная нагрузка М_с= k W ² [21]

На примерах мы будем рассматривать самый распространенный вариант статической нагрузки:   М _с =const (момент сопротивления не зависит от скорости вращения).

Изменение магнитного потока при частотном управлении при принятых допущениях

Рассмотрим, как будет изменяться магнитный поток при законе управления U ₁/ f ₁=const.

Уравнение электрического равновесия:

Допущения в рассуждениях:

- пренебрегаем ЭДС поля рассеяния статора E _1σ=– d Ф_1σ w ₁/ dt =– L _1σ di ₁/ dt (которая по сравнению с основной ЭДС E ₁ мала, так как мал поток рассеяния);

- пренебрегаем активным сопротивлением статора R ₁ (считая его незначительным по сравнению с индуктивным сопротивлением).

В итоге имеем:

Е ₁» U ₁

Основная ЭДС фазы статора кратко (полную формулу см. в Разделе 3 ЭПЛА) может быть записана так:

E ₁ = k Ф f ₁                                                                    (14)

Магнитный поток в воздушном зазоре:

Ф = Е ₁/(kf ₁)» cU ₁/ f ₁.                                                        (15)

Мы видим, что при законе управления U ₁/ f ₁=const, который реализуется при М _с=const обеспечивается (в первом приближении) поддержание постоянного магнитного потока Ф=Ф_ном. При этом двигатель используется наиболее полным образом [12]: и момент создается большой, и ток на его создание расходуется запланированный.

Выражение для потока в общем виде может быть получено из (8) с учетом (15) путем несложных преобразований

(16)

 

Таким образом, если нагрузка уменьшается с уменьшением частоты, то нет смысла сохранять поток двигателя неизменным. Его также можно уменьшать, сохраняя коэффициент перегрузочной способности, то есть запас статической устойчивости. Это приведет к уменьшению потерь в стали двигателя, и повысит экономичность привода с частотным управлением и часто меняющейся нагрузкой по сравнению с асинхронным двигателем при постоянной частоте. Уменьшение потока достигается уменьшением напряжения, еще большим чем при законе U ₁/ f ₁=const [1].

Анализ формулы (15) Ф» c U ₁/ f ₁ показывает, что произойдет, если управление будет производиться лишь одной переменной - напряжением или частотой:

При неизменном напряжении:

1) Уменьшение частоты напряжения (частоты поля статора), как показывает формула (15), приведет к увеличению потока.

Это произойдет вследствие того, что индуктивное сопротивление x_L =2π f ₁ L при снижении частоты f ₁ уменьшится, что приведет при фиксированном напряжении к увеличению намагничивающего тока, значение которого определяет значение магнитного потока. Увеличение магнитного потока приведет к увеличению степени насыщения магнитной цепи; увеличение тока намагничивания – к перегреву АД [46].

2) Увеличение частоты приводит к снижению потока.

Это произойдет вследствие того, что индуктивное сопротивление x_L =2π f ₁ L при увеличении частоты f ₁ увеличится, что приведет при фиксированном напряжении к уменьшению намагничивающего тока, значение которого определяет значение магнитного потока [46]. Уменьшение магнитного потока приведет к снижению максимального момента (уменьшению перегрузочной способности двигателя) и увеличению тока ротора при постоянном моменте нагрузки на валу (М = k Ф I ₂cosj₂) [2].

Оба случая приведут к снижению коэффициента мощности и КПД двигателя, а в ряде случаев к недопустимому нагреву.

Более точные рассуждения о магнитном потоке при малых частотах напряжения см. в п.2.3.5.4.

 

2.3.3. Схемы замещения АД при частотном регулировании

С учетом обозначений, введенных в п.2.3.1, Т-образную схему замещения АД можно представить в виде, представленном на рис.3, а.

На рис.3, б приведена схема, на которой индуктивные сопротивления соответствуют номинальной частоте f _1ном.

Рис. 3. Т-образные схемы замещения АД при частотном регулировании [45]

 

2.3.4. Ограничения по применению базового закона частотного регулирования при больших частотах

При регулировании в диапазоне W>W_ном, т.е. частотах выше номинальной f ₁> f _1ном, закон управления выглядит иначе.

В этом диапазоне, напряжение не повышают выше номинального (U ₁= U _1ном=const).

Итак, базовый закон частотного регулирования относится к регулированию угловой скорости W<W_ном, т.е. для частот напряжения ниже номинальной f ₁< f _1ном.

Почему не повышают напряжение выше номинального?

Номинальное значение любого параметра – это то самое значение, которое учитывают при проектировании всего того, что от этого параметра зависит.

1) В подавляющем большинстве случаев номинальное напряжение равно максимальному напряжению, которое может дать имеющийся источник питания.

Для получения напряжения выше номинального требуется дополнительный регулятор напряжения.

2) На номинальное напряжение рассчитывается обмотка и преобразователь частоты.

При повышении напряжения на обмотке статора выше номинального значения повышается  опасность быстрого старения изоляции.

Что в итоге происходит в интервале W>W_ном?

Напряжение постоянное.

Частоту f ₁ увеличивают пропорционально требуемому увеличению W.

Поток уменьшается Ф<Ф_ном (обратно пропорционально f ₁ и W, формула 15).

Это объясняется тем, что при увеличении частоты возрастает индуктивное сопротивление рассеяния статора x _1σ= k ₁ f ₁ (см. формулу 4), и из-за этого уменьшается ток статора.

Критический момент также уменьшается обратно пропорционально f ₁ и W (формула 6).

Вид механических характеристик при f ₁> f _1ном показан на рис. 4.

 

Рис. 4. Семейство механических характеристик при реализации частотного регулирования

 

Рис. 5. Механические характеристики и допустимый момент нагрузки при частотном регулировании

В диапазоне W>Wном, чтобы мощность АД не превышала допустимую (номинальную), момент двигателя не может оставаться постоянным (да и для сохранения перегрузочной способности этого не требуется) М допΩ =Р доп = Р н = М номΩном = М н Ωном*Ω/Ω. Максимально допустимый момент М при угловых скоростях, выше номинальной Ω>Ωном  будет равен М доп= М нΩном/Ω, то есть будет меньше М ном  (пунктирная линия на рис. 5). Налицо двухзонное регулирование – подобно тому, что мы видели у ДПТ.

Что будет, если мы все же будем работать с нагрузкой М = М _ном?

Анализируем формулу М = k Ф I ₂cosj₂

Поток уменьшился. Момент может быть постоянным только при токе в роторе выше номинального. Что недопустимо.

 

2.3.5. Ограничения по применению базового закона частотного регулирования при малых частотах

2.3.5.1. Ограничение по минимальной скорости, связанное с охлаждением АД

При самовентиляции, когда АД охлаждается с помощью установленного на его валу вентилятора, с уменьшением скорости снижается и эффективность работы вентилятора. Это может привести к перегреву двигателя.

Выход: При длительной работе на пониженных частотах и с номинальным моментом необходимо использовать двигатель, обдуваемый внешним вентилятором, скорость которого не зависит от скорости АД.

Когда обозначенная проблема не стоит даже для АД с самовентиляцией?

Проблема снижения интенсивности охлаждения при малых частотах вращения не является серьезной, если АД на малых скоростях работает с неполной нагрузкой (с малыми потерями).

Существует широкий класс устройств, нагрузка которых зависит от скорости и снижается с уменьшением скорости (или квадрата скорости), например, насосы и вентиляторы. Для таких устройств не существует проблемы перегрева на низкой скорости, как правило, из-за малых потерь в двигателе.

 

2.3.5.2. Проблема, связанная с падением напряжения на активном сопротивлении

Допущения, принятые при выводе базового закона частотного управления (главным образом, пренебрежение активным сопротивлением R ₁), в ряде режимов работы двигателя становятся грубыми и вносят существенные искажения в получаемый результат. То есть не позволяют достичь требуемых показателей, отвечающих заданным критериям эффективности.

 

2.3.5.3. Максимальный (критический) момент

В п. 2.3.1 при выводе базового закона частотного регулирования мы перешли от формулы

(17)

к формуле

(18)

и далее

М макс = k 3 * (U / f)2

(19)

пренебрегая активным сопротивлением статора R ₁.

Погрешность, вносимая при таком переходе, будет незначительна только в том случае, если R ₁<< х _к= х ₁ + х '₂. Величина х _к=2π f ₁ L.  При низких значениях частоты вращения (и частоты f ₁) величина индуктивного сопротивления х _к становится соизмеримой с R ₁, и пренебрежение активным сопротивлением статора становится непозволительно.

В действительности к сопротивлению R ₁ добавляются также и сопротивления преобразователя частоты R _п.ч.

Таким образом, в реальности при соблюдении базового закона частотного управления на малых частотах f ₁ критический момент уменьшается.

 

2.3.5.4. Магнитный поток АД при базовом законе управления

Еще раз запишем уравнение электрического равновесия:

Вновь пренебрегаем ЭДС E _1σ, создаваемой потоком рассеяния.

Учитывая, что E ₁ = k Ф f ₁, получим:

                                                                (20)

При уменьшении частоты второе слагаемое увеличивается, снижая магнитный поток. И это уменьшение магнитного потока будет тем больше, чем больше ток I ₁ (т.е. нагрузка АД).

Таким образом, в реальности при соблюдении базового закона частотного управления на малых частотах f ₁ магнитный поток также не остается постоянным.

Те же рассуждения можно повторить, анализируя Т-образную схему замещения АД. Для наглядности преобразуем схему замещения, приведенную на рис.3, б, поделив все параметры на α. Получим схему, приведенную на рис. 6. Обратите внимания, что в отличие от схем, приведенных в п.2.3.3, здесь изменяется не напряжение, подаваемое в схему, а эквивалентные параметры.

Основной магнитный поток зависит от создающего его намагничивающего тока I _μ, который пропорционален напряжению на ветви намагничивания (на данном рисунке – U_bc) [45].

Рис. 6. Т-образная схема замещения АД [45]

При уменьшении частоты (f 1 и α): - падение напряжения на активном сопротивлении (I 1 r 1/α) увеличивается; - напряжение Ubc (а значит, ток I μ и поток)  уменьшается; - критический момент (вместе с критическим абсолютным скольжением βк) уменьшается (рис. 7, а, б). Пока r 1/α<< х 1σ это уменьшение практически не ощутимо, но с уменьшением f 1 (и α) оно становится все значительнее.

Отметим, что кроме того, магнитный поток не будет оставаться постоянным при изменении нагрузки (момента М _с, а значит, и тока I ₁) при фиксированной частоте. При увеличении нагрузки (тока I ₁) увеличится падение напряжения I ₁ z ₁ в полном сопротивлении статора

                                                                (21)

Это вызовет уменьшение напряжения на ветви намагничивания U_bc, и, следовательно, уменьшения тока намагничивания I _μ и потока.

Изменение магнитного потока (в относительных единицах), о котором говорилось выше, представлено на рис. 7, в.

При фиксированной частоте (f ₁ и α) каждому значению нагрузки М _с соответствует однозначное значение частоты ротора f ₂ и абсолютного скольжения β.

 

а)	б)	в)
Рис. 7.  Изменение критического момента (а), критического абсолютного скольжения (б) и потока при базовом законе частотного регулирования [45]

 

2.3.5.5. Чем грозит обозначенная проблема

Уменьшение в интервале малых частот максимального момента М к, критического абсолютного скольжения и потока приводит к положению механических характеристик, приведенному на рис. 8. Негативные последствия: - снижение перегрузочной способности (М к/ М ном), вызванное уменьшением М к; - уменьшение жесткости механической характеристики, вызванное уменьшением βк;  - (как следствие) снижение стабильности частоты вращения АД при изменении нагрузки, - снижение быстродействия (обусловлено снижением динамического момента за счет снижения момента двигателя и М - М с). - ограничение диапазона регулирования частоты вращения при постоянном моменте сопротивления величиной 3-5 (ограничивается минимально допустимой стабильностью и перегрузочной способностью).

Рис. 8. Механические характеристики АД

Снижение критического момента будет тем больше, чем меньше номинальная мощность двигателя (рис. 7, а). Это связано с тем, что в двигателе большой мощности проводники обмотки статора имеют большое поперечное сечение и, следовательно, значение активного сопротивления обмотки, по сравнению с ее индуктивным сопротивлением, становится все меньше и меньше. И все меньше становится его влияние на электромеханические процессы [45].

2.3.5.6. Допустимый диапазон частот f ₁ при базовом законе

Зависит от минимально допустимой перегрузочной способности.

Пусть при М _с=const допускается снижение перегрузочной способности М _к/ М _ном до 0,8 от М _к.ном/ М _ном. Располагая зависимостью, приведенной на рис. 7, а, можно сделать следующий вывод:

В зависимости от мощности снижение частоты возможно до 0,2 f _ном (большая мощность); 0,4 f _ном (средняя мощность) и 0,53 f _ном (малая мощность).

С учетом этого диапазон регулирования вниз от номинального значения частоты D ≈ f ₁/ f _ном составит 5:1; 2,5:1 и 1,9:1.

В [2] авторы, располагая другим видом характеристик М _к(f ₁), формулируют еще более жесткие ограничения:

Применение закона U ₁/ f ₁=const при М _с=const и допустимой перегрузочной способности 0,8 от номинальной может использоваться:

- для двигателей средней и большой мощности – при изменении частоты не ниже 0,5 f _ном;

- для двигателей малой мощности – при изменении частоты не ниже 0,7 f _ном;

При снижении же частоты напряжения у двигателя средней мощности (14 кВт) до 0,3 f _ном перегрузочная способность снижается до 0,58 от номинального значения [2].

А если нагрузка у АД имеет вентиляторный характер: М _с = k Ω² (рис. 2, в)?

В этом случае ограничений, связанных с уменьшением перегрузочной способности нет. Поэтому закон регулирования U ₁/ f ₁=const в основном используют именно для таких приводов. Теоретически диапазон регулирования здесь равен бесконечности, в реальных приводах к вентиляторному моменту сопротивления добавляется момент сухого трения, и диапазон регулирования снижается и составляет (50…30):1 [45].

 

2.3.6. Уточненный закон частотного управления

Рис. 9. Зависимость U (f) при Мс= const [26]

Для того чтобы АД работал эффективно во всех режимах работы, необходимо корректировать закон U (f) в зависимости от частоты вращения двигателя. При М с=сonst для сохранения постоянства максимального момента с уменьшением частоты требуется увеличивать соотношение U 1/ f 1, то есть с уменьшением частоты снижать напряжение в меньшей степени. Тем самым компенсируется падение напряжения на активном сопротивлении статора. Зависимость U (f) таким образом становится нелинейной (показана на рис. 9 пунктиром).

В этом случае при М _с=сonst закон частотного регулирования U (f) должен обеспечивать на всех частотах постоянство магнитного потока Ф и абсолютного скольжения.

Как уже отмечалось выше (выражение 15): Ф= k _фE₁/ f ₁

То есть для полного использования двигателя наряду с изменением частоты питания f ₁ необходимо пропорционально ей изменять Е ₁ [12].

Е ₁/ f ₁ = const – вот он правильный закон частотного управления при М _с=const.

Вспомним приводимое ранее выражение 16:

(22)

С учетом (15) и (16) в общем виде точный закон частотного регулирования выглядит так:

(23)

Вся проблема состоит в том, что ЭДС Е ₁ является внутренним параметром АД, а воздействовать на двигатель можно лишь напряжением [12].

 

2.3.7. Достигаемые результаты при реализации закона (23) при М _с = const:

1) Неизменный коэффициент перегружаемости М _макс/ М _с;

2) Неуменьшающийся максимальный момент АД обеспечивает высокое быстродействие механизма (вследствие значительного динамического момента).

3) При постоянстве магнитного потока жесткость механических характеристик практически не меняется. Это обуславливает постоянное абсолютное скольжение.

Под абсолютным скольжением будем понимать разность Ω₀-Ω, пропорциональную частоте тока ротора f ₂. В теории частотного управления АД вводят относительную единицу абсолютного скольжения b= (Ω₀-Ω)/Ω_0ном = f ₂/ f _1ном

4) Высокая жесткость механических характеристик обуславливает малые скольжения, а следовательно, небольшой уровень потерь при частотном управлении:

Δ Р _2эл = М *W₀* s

5) Неизменная жесткость механических характеристик и постоянное скольжение обуславливает неизменные потери. В силу их малости, мы получаем практически неизменный (и высокий) КПД во всем диапазоне регулирования.

КПД АД при частотном управлении будет зависеть только от изменения частоты f ₁/ f _1ном и практически не будет зависеть от изменения момента на валу М / М _ном, если насыщение магнитной цепи не слишком велико [8,1].

6)  Неизменный cosφ;

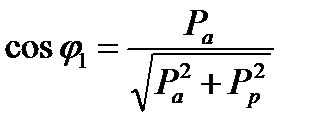
Р _а = М W₀+3 I ₁² R ₁+Δ P _ст – активная мощность; Р _р=3 I _μ² R ₁+3 I ₁² x ₁+3 I ’₂² x '₂ – реактивная мощность.

Поток постоянный, ток I _μ постоянный. Момент постоянный.

7) Диапазон регулирования – до 30 [17].

 

Поделиться:

Воспользуйтесь поиском по сайту: