 |
Нахождение корня уравнения методом Ньютона
|
|
|
|
Данный пример демонстрирует программу, вычисляющую приближенное значение корня уравнения 2x2 – 4x + 1 = 0 на отрезке от 0 до 0. 5 методом Ньютона.
Метод Ньютона позволяет получить приближенное значение корня уравнения, используя итерационный процесс, по следующей формуле:
,
где Xi+1 – следующее приближение (уточненное значение корня), Xi - приближенное значение корня на предыдущем шаге. В качестве начального приближения выбирается та точка отрезка, в которой выполняется условие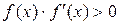 
. В данном примере в качестве начального приближения выбрана точка 0, поскольку 
. В примере итерационный процесс выполняется до тех пор, пока не будет достигнут машинный нуль. Далее представлен текст программы.
CODE SEGMENT ; сегмент команд
ASSUME CS: CODE, DS: DATA, SS: STAC
Start: MOV AX, DATA ; настройка DS
MOV DS, AX ; на сегмент данных
FINIT ; инициализация сопроцессора
FLDZ ; запись в стек начального приближения
; выделение места для предыдущего приближения
FLDZ
M1: FXCH ST(1) ; обмен ST(1) и ST(0)
FADDP ST, ST ; выталкивание из стека значения
FLDZ ; загрузка в стек нуля
FADD ST, ST(1); дублирование предыдущего приближения
FMUL ST, ST ; вычисление xi2
FLD n2 ; загрузка в стек числа 2. 0
FMULP ST(1), ST; вычисление 2xi2
FLD n4 ; загрузка в стек числа 4. 0
FMUL ST, ST(2); вычисление 4xi
FSUBP ST(1), ST; вычисление 2xi2 - 4xi
FLD1 ; загрузка в стек единицы
FADDP ST(1), ST; вычисление 2xi2 - 4xi + 1
FLD n4 ; загрузка в стек числа 4. 0
FMUL ST, ST(2) ; вычисление 4xi
FLD n4 ; загрузка в стек числа 4. 0
FSUBP ST(1), ST ; вычисление 4xi – 4
; вычисление (2xi2 - 4xi + 1) / (4xi – 4)
|
|
|
FDIVP ST(1), ST
; вычисление -(2xi2 - 4xi + 1) / (4xi – 4)
FCHS
; вычисление xi - (2xi2 - 4xi + 1) / (4xi – 4)
FADD ST, ST(1)
; сравнение предыдущего и текущего приближений
FCOM
; загрузка регистра состояния в переменную SW
FSTSW SW
AND SW, 4500H ; наложение маски
CMP SW, 4000H ; проверка на установку флага C3
JNE M1 ; переход, если не достигнут машинный нуль
MOV AX, 4C00H ; функция завершения программы
INT 21H ; вызов DOS
CODE ENDS
DATA SEGMENT ; сегмент данных
n1 DD 1. 0 ; определение промежуточных чисел
n2 DD 2. 0
n4 DD 4. 0
; переменная для хранения значения регистра состояния
SW DW?
DATA ENDS
STAC SEGMENT PARA STACK; сегмент стека
DB 128 DUP (? ) ; область памяти под стек
STAC ENDS
END Start ; точка входа
В начале программы командой FLDZ в стек сопроцессора загружается начальное приближение. На каждой итерации последовательно вычисляются значение функции в точке предыдущего приближения и значение производной функции. После нахождения этих значений вычисляется следующее приближение по формуле, приведенной выше. После нахождения следующего приближения, оно сравнивается с предыдущим. Программа завершает работу, когда текущее и предыдущее приближения равны. Это свидетельствует о достижении машинного нуля. Результат работы программы – приближенное значение корня уравнения – заносится в регистр ST(0).
Для вычисления значения выражения вида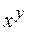 
можно пользоваться следующей формулой перевода: 
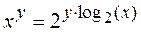, которая вычисляется с использованием команд FYL2X, F2XM1, FSCALE и FPREM.
Для вычисления значений логарифмов можно воспользоваться формулой перевода для логарифмов:
.
Натуральный логарифм можно вычислить по формуле
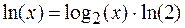
с использованием команд FYL2X и FLDLN2.
Для вычисления значений синуса и косинуса можно воспользоваться следующими тригонометрическими тождествами:
|
|
|
В этих формулах перед знаком радикала должен быть поставлен знак «плюс» или «минус», в зависимости от того, в какой четверти находится значение угла для синуса или косинуса.
Гиперболические синус, косинус и тангенс определяются следующими формулами:
Так как команда FSCALE округляет указываемую степень числа 2 до наименьшего целого числа, то для корректного вычисления значения выражения 
можно использовать следующую формулу
и следующую последовательность команд:
fld y
fld x
fyl2x ; 
fld1
fscale ; 
fxch
fld1
fxch
fprem ;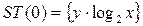 
fmul
f2xm1 ;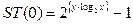 
fld1
fadd ; 
fmul ; 
|
|
|
