 |
Тема. Динамическое программирование
|
|
|
|
Тема. Целочисленное программирование
Рассматриваемые вопросы:
1. Постановка задачи целочисленного программирования
2. Примеры задач
3. Методы решения: алгоритмы и примеры решения
Постановка задачи целочисленного программирования
Задача целочисленного программирования формулируется так же, как и обычная непрерывная ЗЛП, но с дополнительным условием – переменные в оптимальном решении должны быть целыми числами.
Каноническая форма задачи имеет следующий вид:
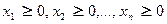
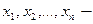целые числа
Дополнительное ограничение целочисленности аргументов резко осложняет задачу и требует развития новых подходов к ее решению, что и составляет предмет целочисленного программирования.
Экономические примеры ЦЗЛП
Задача о контейнере
Имеется n предметов, например ящиков с грузами. Для каждого из них указан вес:
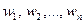
Известна стоимость содержимого груза в в каждом ящике:
.
Требуется загрузить контейнер, грузоподъемность равна W, таким набором предметов, который имел бы максимальную суммарную стоимость.
Для математической записи задачи введем переменные 
, такие что
, если предмет j подлежит загрузке в контейнер
, если не подлежит.
Задача приобретает вид максимизации целевой функции при ограничениях:
Задача о назначениях
Имеется 2 авиалинии и 2 самолета разных типов. Экономический эффект от использования i самолета на линии j составляет величину 
и представлен в таблице:
| Линия | |||
| Тип самолета | |||
Необходимо на каждую линию назначить по одному самолету так, что суммарная прибыль была наибольшей.
Введем переменные 
такие, что:
, если самолет i ставится на линию j;
|
|
|
, в противном случае.
Математически задача приобретает вид:
Первые два ограничения указывают, что каждый самолет назначается на одну линию, другие два ограничения – что на каждую линию назначается один самолет. 
Методы решения ЦЗЛП: метод отсечений
Алгоритм:
1. Решаем ЗЛП без ограничения на целочисленность переменных. Решение целочисленно – алгоритм завершен. Решение не целочисленно – п.2.
2. К задаче добавляется новое ограничение («правильное отсечение» – отсекает найденное на 1 шаге дробное решение, при этом все допустимые целые решения остаются)
Пусть 
− дробная переменная в полученном решении. Выписываем для нее равенство из симплексной таблицы:
Далее вводится новая переменная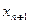 
и на основе равенства строится «отсечение»:
где 
− дробные части коэффициентов.
Добавляем «отсечение» к исходной задаче. Переход к п.1.
Алгоритм повторяется до тех пор, пока не будет получено целочисленное решение. Доказано, что решение может быть получено за конечное число шагов.
Пример:
Методы решения ЦЗЛП: метод ветвей и границ
Идея метода: последовательное деление D на части и определение наиболее перспективной части для исследования.
Алгоритм:
1. Решаем ЗЛП без ограничения на целочисленность переменных.
Решение целочисленное 
– алгоритм завершен. Решение не целочисленное (
− дробная переменная) – п.2. (
– верхняя граница)
2. Делим 
на D1 и D2.
Правило деления:
3. Решение исходной ЗЛП на D1 и D2.
и 
− верхние границы соответствующих задач. Пусть 
. Если при этом 
− целочисленное решение, то оно и будет искомым. Если − дробное, то область 
снова делим на две части 
и 
.
Сначала ветвятся части с наибольшим значением верхней границы, как наиболее перспективные. Однако ветвление остальных частей может потребоваться, если по уже проверенным веткам не окажется целочисленного решения.
|
|
|
Пример:
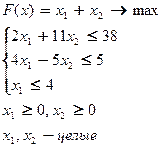
Тема. Динамическое программирование
Рассматриваемые вопросы:
1. Постановка задачи динамического программирования (ЗДП)
2. Принцип оптимальности Беллмана
3. Схема решения ЗДП
4. Экономическое приложение (задача об оптимальном режиме развития фирмы)
|
|
|
