 |
Умножение вектора на скаляр
|
|
|
|
Задача 1.
Определить импульс тела массой 2,0 кг, движущегося со скоростью, модуль которой 5,0 м / с (рис. 10).
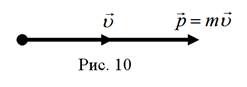
Импульс тела  ; модуль импульса
; модуль импульса  , импульс направлен в сторону скорости
, импульс направлен в сторону скорости  .
.
Задача 2.
Заряд q = −7,5 нКл помещен в электрическое поле с напряженностью, модуль которой E = 400 В/м. Найти модуль и направление силы, действующей на заряд.
Сила равна 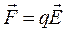 . Так как заряд отрицательный, то вектор силы
. Так как заряд отрицательный, то вектор силы 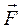 направлен в сторону, противоположную вектору
направлен в сторону, противоположную вектору  (рис. 11).
(рис. 11).
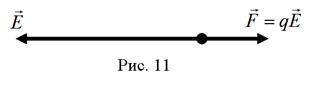
Модуль силы 
 .
.
Задача 3.
Найти работу постоянной силы, модуль которой F = 20 Н, если перемещение S = 7,5 м, а угол α между силой и перемещением α = 120О.
Работа силы равна по определению скалярному произведению силы и перемещения
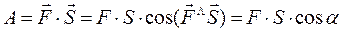
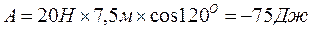 .
.
Задача 4.
Определить силу, действующую на проводник длиной 0,2 м, помещенный в магнитном поле, индукция которого 5 Тл, если сила тока в проводнике 10 А и он образует угол α = 30О с направлением поля.
Сила Ампера:  , где
, где 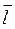 – вектор, модуль которого равен длине проводника, а направление совпадает с направлением электрического тока в проводнике.
– вектор, модуль которого равен длине проводника, а направление совпадает с направлением электрического тока в проводнике.
Модуль силы Ампера:
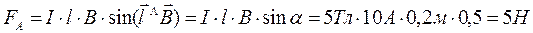 .
.
Задача 5.
Как направлены два вектора, модули которых одинаковы и равны a, если модуль их суммы равен: а) 0; б) 2 а; в) а; г) 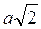 ; д)
; д) 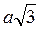 .
.
а) Два вектора направлены вдоль одной прямой в противоположные стороны. Сумма этих векторов равна нулю.

б) Два вектора направлены вдоль одной прямой в одном направлении. Сумма этих векторов равна 2 a.

в) Два вектора направлены под углом 120° друг к другу. Сумма векторов равна a. Результирующий вектор находим по теореме косинусов:
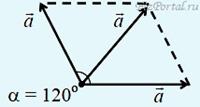
 .
.
г) Два вектора направлены под углом 90О друг к другу. Модуль суммы равен:
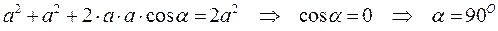 .
.
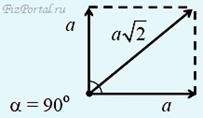
д) Два вектора направлены под углом 60О друг к другу. Модуль суммы равен:
|
|
|
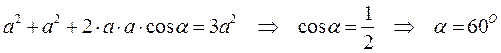 .
.

Ответ: угол α между векторами равен: а) 180О; б) 0; в) 120О; г) 90О; д) 60О.
Задача 6.
Если  , то что можно сказать о взаимной ориентации векторов
, то что можно сказать о взаимной ориентации векторов  и
и 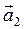 , если: а) a = a 1 + a 2; б) a 2 = a 12 + a 22; в)
, если: а) a = a 1 + a 2; б) a 2 = a 12 + a 22; в) 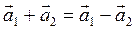 .
.
а) Если сумма векторов находится как сумма модулей этих векторов, то вектора направлены вдоль одной прямой, параллельно друг другу  .
.
б) Если вектора направлены под углом друг к другу, то их сумма находится по теореме косинусов для параллелограмма:
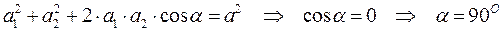 ,
,
вектора перпендикулярны друг другу  .
.
в) Условие 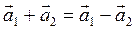 может выполниться, в случае если
может выполниться, в случае если 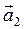 − нулевой вектор, тогда
− нулевой вектор, тогда  .
.
Ответы: а)  ; б)
; б)  ; в)
; в) 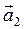 − нулевой вектор.
− нулевой вектор.
Задача 7.
Две силы по 1,42 H каждая приложены к одной точке тела под углом 60О друг к другу. Под каким углом надо приложить к той же точке тела две силы по 1,75 H каждая, чтобы действие их уравновешивало действие первых двух сил?
Первый способ решения
По условию задачи две силы по 1,75 Н уравновешивают две силы по 1,42 Н. Это возможно, если равны модули результирующих векторов пар сил. Результирующий вектор определим по теореме косинусов для параллелограмма. Для первой пары сил:  ,
,
для второй пары сил:  .
.
Приравняв левые части уравнений:
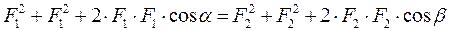
Найдем искомый угол β между векторами:
 .
.
После вычислений:
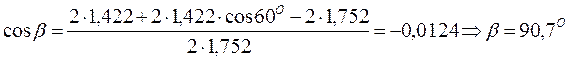 .
.
Второй способ решения
Рассмотрим проекцию векторов на ось координат ОХ (рис.).
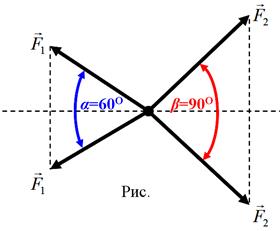
Воспользовавшись соотношением между сторонами в прямоугольном треугольнике, получим
 .
.
Откуда
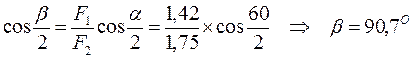 .
.
Задача 8.
Вектор 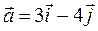 . Какова должна быть скалярная величина c, чтобы
. Какова должна быть скалярная величина c, чтобы  ?
?

Модуль вектора 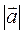 будет равен: a 2 = 32 + 42, и a = ± 5, тогда из c·(±5) = 7,5
будет равен: a 2 = 32 + 42, и a = ± 5, тогда из c·(±5) = 7,5
найдем, что c = ±1,5.
Задача 9.
Угол α между двумя векторами  и
и  равен 60О. Определите длину вектора
равен 60О. Определите длину вектора  и угол β между векторами
и угол β между векторами  и
и  . Модули векторов равны a = 3,0 и b = 2,0.
. Модули векторов равны a = 3,0 и b = 2,0.
Длину вектора, равного сумме векторов  и
и  определим воспользовавшись теоремой косинусов для параллелограмма (рис.).
определим воспользовавшись теоремой косинусов для параллелограмма (рис.).

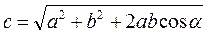
После подстановки
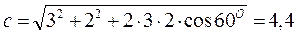 .
.
|
|
|
Для определения угла β воспользуемся теоремой синусов для треугольника ABC:

При этом следует знать, что
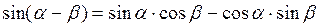 .
.
Решая тригонометрическое уравнение, приходим к выражению
 ,
,
следовательно,
 ,
,
 .
.
Сделаем проверку, воспользовавшись теоремой косинусов для треугольника:
 ,
,
откуда

и
 .
.
Ответ: c = 4,4; β = 23°.
Задача 10.
Для векторов  и
и  , определенных в задаче 9, найдите длину вектора
, определенных в задаче 9, найдите длину вектора 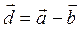 угол γ между
угол γ между  и
и 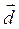 .
.
Задача 11.
Найдите проекцию вектора  на прямую, направление которой составляет угол α = 30О с осью OX. Вектор
на прямую, направление которой составляет угол α = 30О с осью OX. Вектор  и прямая лежат в плоскости XOY.
и прямая лежат в плоскости XOY.
Задача 12.
Вектор  составляет угол α = 30О с прямой АВ, a = 3,0. Под каким углом β к прямой АВ нужно направить вектор
составляет угол α = 30О с прямой АВ, a = 3,0. Под каким углом β к прямой АВ нужно направить вектор  (
(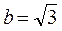 ), чтобы вектор
), чтобы вектор  был параллелен АВ? Найдите длину вектора
был параллелен АВ? Найдите длину вектора  .
.
Задача 13.
11. Заданы три вектора: 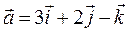 ;
; 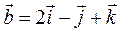 ;
;  . Найдите а)
. Найдите а)  ; б)
; б) 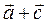 ; в)
; в) 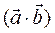 ; г)
; г)  .
.
Задача 14.
Угол между векторами  и
и  равен α = 60°, a = 2,0, b = 1,0. Найдите длины векторов
равен α = 60°, a = 2,0, b = 1,0. Найдите длины векторов 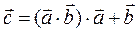 и
и  .
.
Задача 15.
Докажите, что векторы  и
и  перпендикулярны, если
перпендикулярны, если  = {2, 1, −5} и
= {2, 1, −5} и  = {5, −5, 1}.
= {5, −5, 1}.
Задача 16.
Найдите угол α между векторами  и
и  , если
, если  = {1, 2, 3},
= {1, 2, 3},  = {3, 2, 1}.
= {3, 2, 1}.
Задача 17.
Вектор  составляет с осью OX угол α = 30О, проекция этого вектора на ось OY равна ay = 2,0. Вектор
составляет с осью OX угол α = 30О, проекция этого вектора на ось OY равна ay = 2,0. Вектор  перпендикулярен вектору
перпендикулярен вектору  и b = 3,0 (см. рис.).
и b = 3,0 (см. рис.).

Вектор  . Найдите: a) проекции вектора
. Найдите: a) проекции вектора  на оси OX и OY; б) модуль c и угол β между вектором
на оси OX и OY; б) модуль c и угол β между вектором  и осью OX; в)
и осью OX; в) 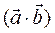 ; г)
; г) 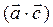 .
.
Задача 18.
Сложить векторы  и
и  , изображенные на рисунке.
, изображенные на рисунке.
 | |||||
 | |||||
 | |||||












Задача 19.
Найти разность векторов, изображенных на рисунке.
 | |||||
 | |||||
 | |||||












Задача 20.
Построить сумму и разность векторов  и
и  .
.
B

 А D
А D
Задача 21.
Даны векторы  и
и  . Построить вектор
. Построить вектор  .
.


 |
Задача 22.
Найти координаты векторов  ,
, 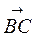 ,
, 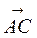 , если А (2; 3), В (̶ 1; ̶ 3), С (̶ 7; 5).
, если А (2; 3), В (̶ 1; ̶ 3), С (̶ 7; 5).
Задача 23.
Даны векторы  = (3;5),
= (3;5),  = (2; ̶ 7). Найти: а)
= (2; ̶ 7). Найти: а) 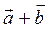 ; б)
; б) 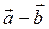 ; в)
; в)  ; г)
; г) 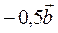 .
.
Задача 24.
В равностороннем треугольнике АВС со стороной, равной 6, найти скалярное произведение векторов: а)  и
и 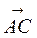 ; б)
; б)  и
и 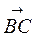 .
.
Задача 25.
Найти угол между векторами а)  и
и 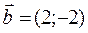 ; б)
; б)  и
и 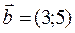 .
.
Задача 26.
Найти углы треугольника с вершинами А (6; 7), В (3; 3), С (1; ̶ 5).
|
|
|


