 |
Практическая работа №2 Определение режима течения различных жидкостей.
|
|
|
|
Практическая работа №2 Определение режима течения различных жидкостей.
Цель работы – приобрести практические навыки по определению режимов движения реальных жидкостей, приобрести умения анализировать произведенные расчеты параметров для заданных условий.
Теоретическая часть
Существуют два режима движения жидкостей: ламинарный и турбулентный.
При ламинарном режиме течения частицы жидкости перемещаются по траекториям, направленным вдоль потока без поперечного перемещения. Поток жидкости образуется как бы отдельными параллельными слоями; пульсации скорости потока и давления жидкости отсутствуют.
При турбулентном режиме течения частицы жидкости перемещаются по случайным хаотическим траекториям. Турбулентное течение сопровождается постоянным перемещением жидкости, характеризуется наличием пульсации скорости потока и давления жидкости.
Опытами было установлено, что наличие того или иного режима течения жидкости определяется: средней скоростью потока жидкости; характерным линейным размером сечения потока жидкости (для труб – диаметром) и кинематической вязкостью жидкости.
Исследования О. Рейнольдса показали, что режим движения жидкости в общем случае зависит от скорости движения, размеров потока, плотности и
вязкости жидкости. Комплекс указанных величин, характеризующий режим движения жидкости называют числом Рейнольдса:
Re = (р 
J R)/µ, (1. 1)
где R- гидравлический радиус потока; µ- динамическая вязкость; J- скорость потока жидкости м/с; р- давление жидкости, мПа
Число Рейнольдса - величина безразмерная.
Так как кинематическая вязкость представляет собой отношение динамической жидкости к её плотности, т. е.
|
|
|
Re= (J R)/ν (1. 2)
где ν - кинематическая вязкость, м2/с.
Эту формулу применяют при определении числа Рейнольдса для потока любого сечения.
Для круглых цилиндрических с внутренним диаметром d, мм:
Red=(J d)/ν (1. 3)
Поскольку для таких труб гидравлический радиус R=4 d, то
Re=4 Red (1. 4)
Число Рейнольдса можно выразить также через расход Q, м3 /с жидкости из условия Q=J S, следовательно
J = Q/S=4Q/(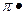 
d2 ) (1. 5)
Re=(4 Q d)/(π d2 ν )=(1, 27 Q)/(d ν ) (1. 6)
При Q - в л/мин, d- в мм, ν - в мм2/с
Re=1, 27(1, 67 10-5)/(10-3 10-6) Q/(d ν )=21200 Q(d ν ) (1. 7)
Границы существования режимов движения жидкости определяются двумя критическими значениями Рейнольдса: нижнем Reкр и верхнем Re/кр. При Rе≤ Reкр наблюдается устойчивый ламинарный режим течения жидкости, при Rе ≥ Re/кр- устойчивый турбулентный режим. В интервале число Рейнольдса Re/кр ≥ Rе ≥ Reкр режим течения жидкости неустойчив: ламинарный режим легко переходит в турбулентный.
В настоящее время принимают нижнее критическое число Рейнольдса равным Reкр=250…500; для цилиндрических труб Redкр=1000…2000. При проведении гидравлических расчётов очень часто принимают Re/кр =575 и Redкр =2300.
На практике часто наблюдается турбулентный режимов движения жидкости, например, при движении воды в трубах из-за её сравнительно малой вязкости и большой скорости течения. При движении вязких жидкостей (нефть, масло и др. ), а также при движении жидкостей с малой вязкостью, но с небольшой скоростью, наблюдается ламинарный режим течения.
Скорость жидкости J, м/с определяется по формуле:
J=Q/ S = Q •4 /( π d2), (1. 8)
где Q- расход жидкости, л/с;
d- диаметр трубы, м.
При протекании по трубопроводу жидкость испытывает сопротивление, зависящее от длины трубы, шероховатости её внутренних поверхностей, площади и формы её поперечного сечения. Что вызывает потери давления.
В общем случае потери давления (Па) в трубах круглого сечения определяются по формуле Дарси- Вейсбаха:
|
|
|
∆ pл= λ (L/d) (J2/2) p, (1. 9)
где λ - коэффициент гидравлического трения; L- длина трубы, м; d- внутренний диаметр трубы, м.
Для ламинарного трения жидкости коэффициент гидравлического трения:
λ 
=A/Re, (1. 10)
где А можно иметь значение от 64 до 150 (например, в идеальном случае при изотермическом потоке А=64; при течении потока в реальных металлических трубах и гибких рукавах А=75…85; при небольшом изгибе рукавов А=108; если поток движения по трубам, изогнутым на 90°, то А=75; при изгибе труб более 90°А=80; если поток движения по смятой на 40…50% трубе, то А=150.
Для турбулентного течения коэффициент гидравлического трения
λ T=0, 3164/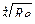 
(1. 11)
Потери давления при ламинарном течении являются линейной функцией скорости (так как в выражении Re содержится скорость), а при турбулентном течении - скорости в степени 1…2.
|
|
|
