 |
Полный программный код проекта.
|
|
|
|
КУРСОВАЯ РАБОТА
ПО ИНФОРМАТИКЕ
Выполнил: студент гр. БИК 1105
Семикин А.С.
Проверил: Сосновиков Г.К.
Москва 2013
СОДЕРЖАНИЕ
Индивидуальное задание......................................................................................
Постановка задачи...................................................................................................
Упрощенный алгоритм решения задачи.................................................................
Обоснование методов решения...............................................................................
Описание методов решения...................................................................................
Тестирование методов.............................................................................................
Полный программный код проекта.........................................................................
Результаты программы............................................................................................
Полное решение с помощью пакета MathCad.......................................................
Вывод…...................................................................................................................
Используемая литература…..................................................................................
Индивидуальное задание.
Заданы функции 
и 
Найти оптимальное значение параметра a2 = a2* по критерию
d – абсцисса точки пересечения графиков функци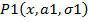й 
и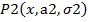 
; а1 = 2; с=1; e = 4.
Постановка задачи.
В курсовой работе требуется найти максимум функции 
, которая представляет собой сумму интегралов. Предел интегрирования d представляет собой корень уравнения 
= 
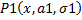, который тоже зависит от параметра а2. Т.о. для решения задания нам требуется с помощью одного из методов одномерной оптимизации вычислить максимум функции на отрезке, решая на каждом шаге уравнение и вычисляя значение суммы интегралов. Максимум функции будем искать на отрезке (0, 6), т.к. корень уравнения =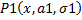 
равняется d = 1 + a/2, а d заключено в пределах от 1 до 4. Т.о. максимум функции a2 лежит на отрезке (0; 6).
|
|
|
Решение данной задачи требует использование следующих численных методов:
· метод одномерной оптимизации
· численное интегрирование
· решение уравнений
Последовательность решения задачи показано ниже в виде укрупнённой схемы алгоритма:
 |
Выбор и обоснование используемых методов решения.
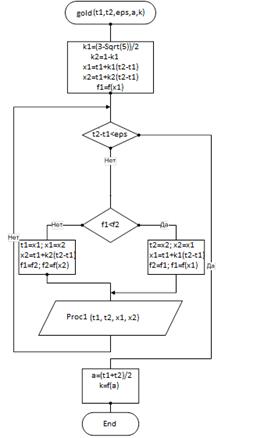
1. Для решения задачи одномерной оптимизации будет использован метод золотого сечения: Этот метод эффективен с точки зрения количества вычислений функций на отдельной итерации, хотя проигрывает методу дихотомии по количеству требуемых итераций для достижения заданной точности. 2. Для проведения численного интегрирования выберем метод Симпсона:
Так как в состав наших подынтегральных функции входит нелинейные, поэтому большей точностью будет обладать метод Симпсона.
3. Для решения нелинейного уравнения выберем метод половинного деления:
Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых. Последнее является преимуществом, т.к. вычисление производной сложной функции достаточно проблематично.
Описание методов решения.
Метод золотого сечения.
В основу метода положено разбиение отрезка неопределенности [a;b] в соотношении золотого сечения, такого, что отношение длины его большей части ко всей длине отрезка равно отношению длины его меньшей части к длине его большей части:
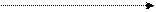
l
l2 l1
где k1, k2 - коэффициенты золотого сечения.
В методе золотого сечения каждая точка (х1 и х2)осуществляет золотое сечение отрезка.
или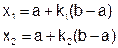 
Точка х1 осуществляет золотое сечение не только отрезка [a;b], но и отрезка [a;х2]. Точно так же точка х2 осуществляет золотое сечение не только отрезка [a;b], но и отрезка [х1;b]. Это приводит к тому, что значение целевой функции на каждой итерации (кроме первой) вычисляется один раз.
|
|
|
Сокращение отрезка неопределенности следующим образом:
1) если f(x1) £ f(x2), то x*Î[a0;x2]
2) если f(x1) > f(x2), то x*Î[x1;b0]
После каждой итерации длина отрезка неопределенности сокращается в 1.618 раза. Длина конечного отрезка неопределенности Dn = 0.618nD0, где D0= (b-a) – начальная длина отрезка.
Условие окончания процесса итераций Dn 
e. Отсюда можно найти количество итераций, необходимое для достижения точки минимума:
отсюда 
или 
Формула Симпсона.
Для получения формулы Симпсона применяется квадратичный интерполирующий полином. За элементарный интервал интегрирования принимается отрезок [xi;xi+2]. Поэтому интервал интегрирования [a;b] разбивается наn отрезков, где n=2m – четное число (рис.2).
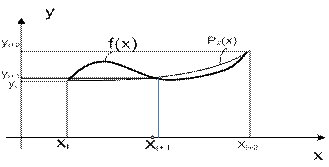
Для всего интервала интегрирования [a;b] формула Симпсона выглядит следующим образом: 
Тестирование процедур.
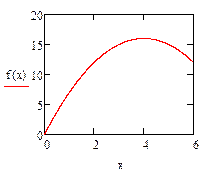
Для проверки правильности процедуры, реализующей метод золотого сечения, в качестве теста используем функцию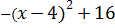 
, имеющую на отрезке [0;6] единственный минимум Xmin= 4, а значение функции в этой точке f(Xmin)=16.
Проведем проверку правильности тестовых данных с использованием средств пакета MathCad:
|
|
|
|
|
Код программы:
Option Strict On
Option Explicit On
Imports System.Math
Public Class Form6
'процедура ввода
Sub vvod(ByVal t As TextBox, ByRef x As Double)
x = Val(t.Text)
End Sub
'процедура вывода
Sub vivod(ByVal x As Double, ByVal T As TextBox)
T.Text = CStr(x)
End Sub
'целевая функция
Function f(ByVal x As Double) As Double
Return -((x - 4) ^ 2) + 16
End Function
'метод золотого сечения на отрезке [o1,o2]
'а2-оптимальное значение параметра
Sub gold(ByVal o1 As Double, ByVal o2 As Double, ByVal Eee As Double, _
ByRef a2 As Double, ByRef k As Double, ByRef z As String)
Dim k1, k2, x1, x2, f1, f2 As Double
k1 = (3 - Sqrt(5)) / 2
k2 = 1 - k1
x1 = o1 + k1 * (o2 - o1)
x2 = o1 + k2 * (o2 - o1)
f2 = f(x1)
z = ""
Do Until (o2 - o1) < Eee
If (-f1) < (-f2) Then
o2 = x2: x2 = x1
x1 = o1 + k1 * (o2 - o1)
f2 = f1
f1 = f(x1)
Else
o1 = x1: x1 = x2: f1 = f2
x2 = o1 + k2 * (o2 - o1)
f2 = f(x2)
End If
z = z + Format(o1, "0.00000") + Space(3) + Format(o2, "0.00000") + Space(3) + Format(x1, "0.00000") + Space(3)
z = z + Format(x2, "0.00000") + Space(5) + Format(f1, "0.00000") + Space(5) + Format(f2, "0.00000") + Space(4) + Format(o2 - o1, "0.00000") + vbNewLine
Loop
a2 = (o1 + o2) / 2
k = f(a2)
End Sub
Private Sub Button12_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button12.Click
Dim z As String = ""
vvod(TextBox13, Eee)
vvod(TextBox14, o1)
|
|
|
vvod(TextBox15, o2)
gold(o1, o2, Eee, a2, k, z)
TextBox16.Text = z
vivod(a2, TextBox17)
vivod(k, TextBox18)
End Sub
Private Sub Button13_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button13.Click
Form5.Show()
Me.Hide()
End Sub
Private Sub Button14_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button14.Click
Form7.Show()
End Sub
End Class
Результат выполнения:
Результаты, полученные при тестировании, совпадают с истинными. Программа работает верно.
Метод Симпсона.
Для проверки правильности процедуры, реализующей метод Симпсона, в качестве теста используем интеграл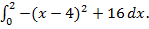 
|
Схема алгоритмов:
Код программы:
Option Strict On
Option Explicit On
Imports System.Math
Public Class Form7
'процедура ввода
Sub vvod(ByVal t As TextBox, ByRef x As Double)
x = Val(t.Text)
End Sub
'процедура вывода
Sub vivod(ByVal x As Double, ByVal T As TextBox)
T.Text = CStr(x)
End Sub
'целевая функция
Function f(ByVal x As Double) As Double
Return -((x - 4) ^ 2) + 16
End Function
Sub reshenie1i(ByVal a As Double, ByVal b As Double, ByVal Eee As Double, ByRef I1 As Double)
Dim n, i, ccc As Integer
Dim h, s1, x As Double
n = 2
h = (b - a) / n
I1 = (f(a) + 4 * f((a + b) / 2) + f(b)) * h / 3
Do
n = n * 2
h = (b - a) / n
s1 = I1
ccc = 4
x = a
I1 = f(a) + f(b)
For i = 1 To n - 1
x = x + h
I1 = I1 + ccc * f(x)
ccc = 6 - ccc
Next
I1 = I1 * h / 3
Loop Until Abs(I1 - s1) / 15 < Eee
End Sub
Private Sub Button15_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button15.Click
Dim a, b, Eee, I1 As Double
vvod(TextBox19, Eee)
vvod(TextBox20, a)
vvod(TextBox21, b)
reshenie1i(a, b, Eee, I1)
vivod(I1, TextBox22)
End Sub
Private Sub Button16_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button16.Click
Form6.Show()
Me.Hide()
End Sub
Private Sub Button17_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button17.Click
Form8.Show()
End Sub
End Class
Результат выполнения:
Результаты, полученные при тестировании, совпадают с истинными. Программа работает верно.
Метод половинного деления.
Для проверки правильности процедуры, решим уравнение –(x-4)^2+16 = 0
|
|
|
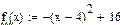
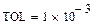
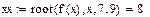
Схема алгоритмов:
Код программы:
Option Strict On
Option Explicit On
Imports System.Math
Public Class Form8
'процедура ввода
Sub vvod(ByVal t As TextBox, ByRef x As Double)
x = Val(t.Text)
End Sub
'процедура вывода
Sub vivod(ByVal x As Double, ByVal T As TextBox)
T.Text = CStr(x)
End Sub
'целевая функция
Function f(ByVal x As Double) As Double
Return -((x - 4) ^ 2) + 16
End Function
'решение уравнения
Sub reshenieUr(ByVal с As Double, ByVal ee As Double, ByVal Eee As Double, ByRef Xx As Double)
|
|
|
Dim Cc, EEEe, f1, f2, f3 As Double
Dim n As Integer
Cc = c
EEEe = ee
n = 0
Do
n = n + 1
Xx = (Cc + EEEe) / 2
f1 = f(Cc)
f2 = f(Xx)
f3 = f(EEEe)
If (f2 * f3 < 0) Then
Cc = Xx
Else
EEEe = Xx
End If
Loop Until Abs(EEEe - Cc) < Eee
End Sub
Private Sub Button18_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button18.Click
Dim c, ee, Xx, Eee As Double
vvod(TextBox24, Eee)
vvod(TextBox26, c)
vvod(TextBox23, ee)
reshenieUr(c, ee, Eee, Xx)
vivod(Xx, TextBox25)
End Sub
Private Sub Button19_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button19.Click
Form7.Show()
Me.Hide()
End Sub
Private Sub Button20_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button20.Click
End
End Sub
End Class
Результат выполнения:
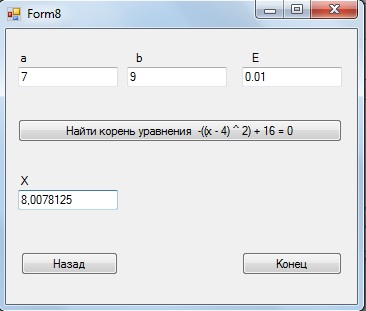
Результаты, полученные при тестировании, совпадают с истинными. Программа работает верно.
Полный программный код проекта.
'программный код 1 формы
Public Class Form1
Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
Form2.Show()
End Sub
End Class
'программный код 2 формы
Public Class Form2
Private Sub Form2_Load(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles MyBase.Load
TextBox3.Text = "1"
TextBox4.Text = "4"
TextBox5.Text = "0.01"
TextBox6.Text = "0"
TextBox7.Text = "6"
End Sub
Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click
Form1.Show()
Me.Hide()
End Sub
Private Sub Button6_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button6.Click
vvod(TextBox3, c)
vvod(TextBox4, ee)
vvod(TextBox5, Eee)
vvod(TextBox6, o1)
vvod(TextBox7, o2)
Form4.Show()
End Sub
End Class
'программный код 3 формы
Public Class Form4
Private Sub Button8_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button8.Click
Form2.Show()
Me.Hide()
End Sub
Private Sub Button9_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button9.Click
Form5.Show()
End Sub
Private Sub Button7_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button7.Click
Dim z As String = ""
gold(o1, o2, Eee, a2, k, z)
TextBox8.Text = z
vivod(a2, TextBox9)
vivod(k, TextBox10)
End Sub
End Class
'программный код 4 формы
Public Class Form5
Private Sub Form5_Load(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles MyBase.Load
vivod(a2, TextBox12)
vivod(k, TextBox11)
End Sub
Private Sub Button11_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button11.Click
End
End Sub
Private Sub Button10_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button10.Click
Form4.Show()
Me.Hide()
End Sub
Private Sub Button15_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button15.Click
Form6.Show()
End Sub
End Class
'программный код модуля
Option Strict On
Option Explicit On
Imports System.Math
Module Module1
Public Eee As Double 'точность
Public si1 As Double 'сигма1
Public si2 As Double 'сигма2
Public c As Double 'нижний предел интегрирования
Public ee As Double 'верхний предел интегрирования
Public Xx As Double 'абсцисса пересечения графиков функций
Public o1 As Double 'границы отрезка, содержащего максимум
Public o2 As Double 'границы отрезка, содержащего максимум
Public a2 As Double 'оптимальное значение а
Public k As Double 'максимальное значение функции
'процедура ввода
|
|
|
Sub vvod(ByVal t As TextBox, ByRef x As Double)
x = Val(t.Text)
End Sub
'процедура вывода
Sub vivod(ByVal x As Double, ByVal T As TextBox)
T.Text = CStr(x)
End Sub
'поиск абсциссы точки пересечения графиков функций
Function fu(ByVal x As Double, ByVal a As Double) As Double
Return (2 / ((2 * PI) ^ (1 / 2))) * (E ^ (-2 * ((x - 2) ^ 2)) - E ^ (-2 * ((x - a) ^ 2)))
End Function
'поиск абсциссы точки пересечения графиков функций
Sub reshenieUr(ByVal a As Double, ByRef Xx As Double)
Dim Cc, EEEe, f1, f2, f3 As Double
Dim n As Integer
Cc = c
EEEe = ee
n = 0
Do
n = n + 1
Xx = (Cc + EEEe) / 2
f1 = fu(Cc, a)
f2 = fu(Xx, a)
f3 = fu(EEEe, a)
If (f2 * f3 < 0) Then
Cc = Xx
Else
EEEe = Xx
End If
Loop Until Abs(EEEe - Cc) < Eee
End Sub
'вычисление значения интегралов
Function f1i(ByVal x As Double) As Double
Return (2 / ((2 * PI) ^ (1 / 2))) * (E ^ (-2 * ((x - 2) ^ 2)))
End Function
'вычисление значения интегралов
Function f2i(ByVal x As Double, ByVal a As Double) As Double
Return (2 / ((2 * PI) ^ (1 / 2))) * (E ^ (-2 * ((x - 2.1) ^ 2)))
End Function
'вычисление значения интегралов
Sub reshenie1i(ByVal d As Double, ByRef I1 As Double)
Dim n, i, ccc As Integer
Dim h, s1, c, x As Double
c = 1
n = 2
h = (d - c) / n
I1 = (f1i(c) + 4 * f1i((c + d) / 2) + f1i(d)) * h / 3
Do
n = n * 2
h = (d - c) / n
s1 = I1
ccc = 4
x = c
I1 = f1i(c) + f1i(d)
For i = 1 To n - 1
x = x + h
I1 = I1 + ccc * f1i(x)
ccc = 6 - ccc
Next
I1 = I1 * h / 3
Loop Until Abs(I1 - s1) / 15 < Eee
End Sub
'вычисление значения интегралов
Sub reshenie2i(ByVal d As Double, ByVal a As Double, ByRef I2 As Double)
Dim n, ccc, i As Integer
Dim h, s1, ee, x As Double
ee = 4
n = 2
h = (ee - d) / n
I2 = (f2i(d, a) + 4 * f2i((d + ee) / 2, a) + f2i(ee, a)) * h / 3
Do
n = n * 2
h = (ee - d) / n
s1 = I2
ccc = 4
x = c
I2 = f2i(d, a) + f2i(ee, a)
For i = 1 To n - 1
x = x + h
I2 = I2 + ccc * f2i(x, a)
ccc = 6 - ccc
Next
I2 = I2 * h / 3
Loop Until Abs(I2 - s1) / 15 < Eee
End Sub
'метод золотого сечения на отрезке [o1,o2]
'а2-оптимальное значение параметра
Sub gold(ByVal o1 As Double, ByVal o2 As Double, ByVal Eee As Double, _
ByRef a2 As Double, ByRef k As Double, ByRef z As String)
Dim k1, k2, x1, x2, f1, f2, Xx, d, I1, I2, IS11, IS21, IS12, IS22 As Double
k1 = (3 - Sqrt(5)) / 2
k2 = 1 - k1
x1 = o1 + k1 * (o2 - o1)
x2 = o1 + k2 * (o2 - o1)
reshenieUr(x1, Xx)
d = Xx
reshenie1i(d, I1)
IS11 = I1
reshenie2i(d, x1, I2)
IS21 = I2
f1 = -IS11 - IS21
reshenieUr(x2, Xx)
d = Xx
reshenie1i(d, I1)
IS12 = I1
reshenie2i(d, x2, I2)
IS22 = I2
f2 = IS12 + IS22
z = ""
Do Until (o2 - o1) < Eee
If (-f1) < (-f2) Then
o2 = x2: x2 = x1
x1 = o1 + k1 * (o2 - o1)
f2 = f1
reshenieUr(x1, Xx)
d = Xx
reshenie1i(d, I1)
IS11 = I1
reshenie2i(d, x1, I2)
IS21 = I2
f1 = IS11 + IS21
Else
o1 = x1: x1 = x2: f1 = f2
x2 = o1 + k2 * (o2 - o1)
reshenieUr(x2, Xx)
d = Xx
reshenie1i(d, I1)
IS12 = I1
reshenie2i(d, x2, I2)
IS22 = I2
f2 = IS12 + IS22
End If
z = z + Format(o1, "0.00000") + Space(3) + Format(o2, "0.00000") + Space(3) + Format(x1, "0.00000") + Space(3)
z = z + Format(x2, "0.00000") + Space(5) + Format(f1, "0.00000") + Space(5) + Format(f2, "0.00000") + Space(4) + Format(o2 - o1, "0.00000") + vbNewLine
Loop
a2 = (o1 + o2) / 2
reshenieUr(a2, Xx)
d = Xx
reshenie1i(d, I1)
IS11 = I1
reshenie2i(d, a2, I2)
IS21 = I2
k = IS11 + IS21
End Sub
End Module
Результаты программы.
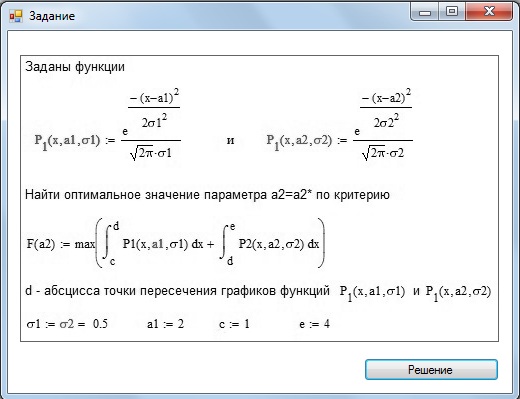
Форма с заданием.
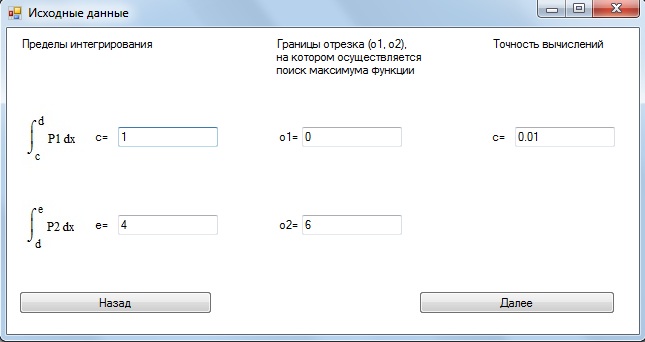
Форма с исходными данными.
Форма с решением.
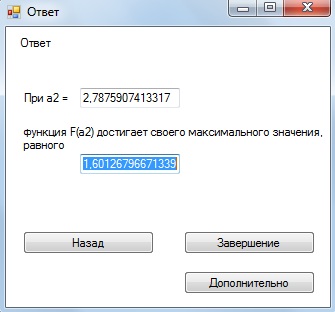
Форма с ответом.
|
|
|
