Использование ресурсов

теорема

о маргинальных

значениях

Многое в поведении животных можно описать с помощью математических методов (см., например, теория оптимального фуражирования). Один из таких аспектов поведения можно выразить простым вопросом: как долго животному имеет смысл добывать корм на одном участке и когда ему уже пора перейти в другое место? Какая стратегия позволяет максимально увеличить его общее энергопотребление?

Это типичная задача для теории игр — раздела математики, в котором для выработки стратегий, позволяющих максимально повысить шансы выигрыша в игре, используется метод вероятностного рассуждения. Эта теория применима и к обычным азартным играм вроде покера, и к таким «играм», как военная стратегия, расположение торговых представительств и размещение рекламы. Эти же методы применяются и для изучения стратегии фуражирования.

Когда животное приходит на новый участок, оно начинает потреблять ресурсы, которые оно там нашло. Представьте лошадь, которая зашла на лужайку с высокой травой, или лисицу, которая оказалась в местности, изобилующей грызунами. Приступив к потреблению этих ресурсов, животное начинает получать энергию. Вначале количество получаемой энергии будет резко расти, поскольку потребление энергии животным подскакивает от нуля (во время поиска энергоресурсов) до того количества, которое оно получает на этом новом участке. Однако по мере того, как животное потребляет эти ресурсы, общее количество полученной энергии достигает определенного стабильного уровня. Когда все ресурсы будут исчерпаны, энергопотребление вновь упадет до нуля и общая энергия, получаемая на данном участке, будет оставаться на постоянном уровне. Вопрос заключается в следующем: когда наступает наилучший момент для животного, чтобы двинуться дальше, оставив некоторое количество неиспользованных ресурсов, и идти вперед, чтобы найти новую ресурсную базу? Ответ на этот вопрос дает теорема о маргинальных значениях, предложенная в 1966 году американским экологом Эриком Л. Чарновом (Eric L. Charnov, р. 1947).

Теорема учитывает время, затраченное на переход от одной ресурсной базы к другой, — назовем его временем перемещения. Время, в течение которого животное остается в определенной ресурсной области, назовем временем пребывания. Оптимальная стратегия — та, которая позволяет максимально увеличить общее потребление энергии с течением времени. Если животное получает энергию E за данное время пребывания, то общая скорость энергопотребления за все время t (включающее время перемещения плюс время пребывания) будет равна E, деленному на t.

Давайте начнем с предположения, что ресурсы на всех участках одинаковые — например, что все лужайки с травой одинаково

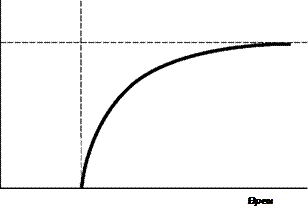Животное, нашедшее новый пищевой ресурс, вначале получает большое количество энергии, но по мере того, как ресурс истощается, лучшей стратегией для животного будет идти вперед в поисках нового ресурса. Вертикальная пунктирная линия — начало потребления животным пищевого ресурса, горизонтальная пунктирная линия — максимальный уровень энергопотребления

зеленые. Математическая теория игр утверждает, что животное максимально увеличит общее получение энергии во времени, если оно будет покидать каждый участок, как только скорость получения энергии в ней достигнет максимума. Иными словами, время идти дальше наступает именно тогда, когда все идет наилучшим образом. Если животное останется на месте, это позволит ему действительно получить больше энергии от известного источника, но общее количество энергии, которое оно приобретет, будет меньшим, чем оно получило бы, если бы ушло на другой участок немедленно.

Что же происходит в реальной ситуации, когда участки различаются по количеству ресурсов? Теорема утверждает, что лучшая стратегия для животного — покидать каждую область, независимо от ее богатства, как только скорость получения энергии упадет до максимума, который может дать средний участок. Таким образом, оптимальный момент для оставления участка наступает тогда, когда маргинальное (предельное) значение скорости получения энергии достигает этой средней скорости потребления (отсюда и название теоремы).

Теорема прогнозирует, что потребители питательных веществ будут проводить меньше времени на лужайках, где меньше пищи. Далее следует, что эти потребители будут уходить с таких лужаек быстрее, если лужайки расположены близко друг к другу, чем когда они находятся далеко друг от друга. Потребители также будут покидать такие лужайки быстрее, если они расположены в местности, изобилующей кормами, чем если этот участок небогат кормом.

По поводу такого подхода к объяснению поведения животных необходимо сделать одно замечание. Никто не предполагает, конечно, что животное садится с калькулятором и высчитывает скорость своего энергопотребления. Если рассуждать с позиций теории эволюции, то теорема о маргинальных значениях говорит нам, что если животное случайно найдет оптимальную стратегию, то оно будет иметь больше шансов передать свои гены следующему поколению. В конце концов через какое-то время животные придут к своей оптимальной стратегии, даже ни разу не задумавшись о ней.

В этом смысле эволюция во многом похожа на «невидимую руку» в теории экономических рынков шотландского экономиста

Адама Смита, бытовавшую в XVIII веке. Действуя за сценой, она способствует такому поведению, которое приносит максимальную выгоду. Классический «экономический человек», согласно этой теории, действует абсолютно рациональным образом с полным знанием рынка и не имеет никакого сходства с реальным человеком, чье поведение будет предпочтительным и в итоге — преобладающим. Аналогичным образом животные, которые не перемещаются из одной области в другую в соответствии с теоремой о маргинальных значениях, будут в среднем менее удачливыми, чем те, которые перемещаются. В конечном счете всегда побеждает стремление к действию.