 |
Решение вычислительных задач математики. Приближенное вычисление определенных интегралов. Понятие стиля программирования.
|
|
|
|
Лабораторная работа № 1
В этой работе изучается программирование классических методов приближенного вычисления определенных интегралов: метод прямоугольников, метод трапеций и метод парабол (метод Симпсона)
2.1. Квадратурные формулы
а) Постановка задачи.
Пусть, в точках 
, расположенных на отрезке 
, известны значения 
интегрируемой на отрезке 
функции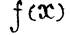 
. Требуется исходя из этих значений приближенно вычислить 
Для решения поставленной задачи примем точки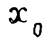 
….. 
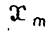в качестве узлов интерполяции функции 
и аппроксимируем ее полиномом Лагранжа:
(2.1)
Тогда
(2.2)
где 
- погрешность приближенного метода.
Очевидно, исходя из формулы (I.I) получаем
(2.3)
где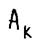 
- некоторые постоянные, зависящие только от 
.... 
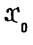Таким образом, формула (2.2) приближенного интегрирования принимает вид
(*)
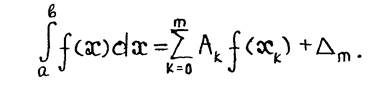Определение 2.1. Формула (*), в которой коэффициенты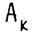 
зависят от узлов 
(но не от 
), называется квадратурной приближенной формулой для исходного интеграла.
Теоретически полиномом Лагранжа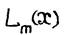 
можно приблизить
функцию 
сколь угодно точно, если она достаточно гладкая,
а степень 
достаточно велика. Следовательно, интеграл по формуле (*) также можно, вычислить сколь угодно точно. Однако с увеличением 'степени 
резко увеличивается трудоемкость счета, поэтому применять квадратурные формулы (*) при больших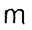 
невыгодно. Наиболее употребительные случаи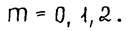 
а) Случай 
. Интерполяция постоянной
В этом случае точка 
является единственной точкой интерполяции, причем 
Соответствующая квадратурная формула имеет вид
Обычно полагают 
или 
(середина отрезка 
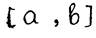). Тогда
(2.4)
Эта формула называется формулой прямоугольников.
б) Случай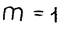 
. Линейная интерполяция
|
|
|
В этом случае 
аппроксимируется линейной функцией:
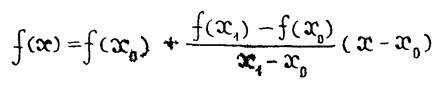
Полагая 
, 
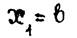, получаем, в частности, формулу
(2.5)
Эта формула называется формулой трапеций.
в) Случай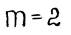 
. Параболическая интерполяция
В этом случае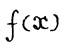 
аппроксимируется квадратичным трехчленом:
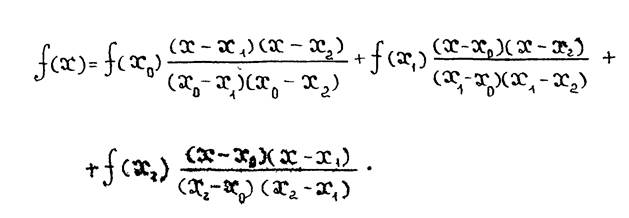
Положим 
Тогда подсчет приводит к приближенной формуле
(2.6)
Эта формула называется формулой парабол или формулой Симпсона.
2.2. Оценка погрешности
Пусть в соответствии с равенством (2.2) 
и 
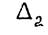- погрешности формул (2.4),(2.5) и (2.6) соответственно.
Имеет место следующая теорема.
Теорема 2.1.
Пусть 
Тогда
Пусть 
Тогда
Пусть 
Тогда
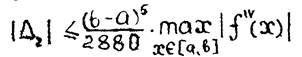
Доказательство теоремы проведем для случая 
. Имеем
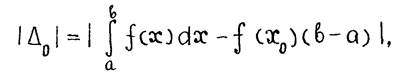(2.7)
где 
- середина отрезка 
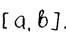
Далее, по формуле Тейлора
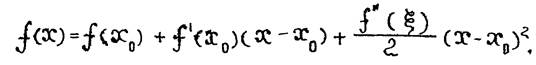
где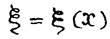 
- некоторая точка между 
и 
Следовательно,
Сравнивая эту формулу с формулой (2.7), получаем, что
откуда, вычисляя последний интеграл, немедленно приходим к искомой оценке в п.1 теоремы.
С доказательством оценки погрешности для случаев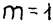 
и 
можно ознакомиться [2].
Вывод. Итак, мы видим, что если отрезок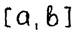 
мал, то и погрешность приведенных формул достаточно мала. При этом наилучшей по порядку степени является формула, соответствующая квадратичной интерполяции функции 
Однако, если отрезок 
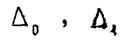не является малым, то и погрешности 
и 
также не малы, и, следовательно, (2.4) - (2.6) не дают хорошей точности.
В этом случае поступают так: отрезок 
разбивается на сумму достаточно малых отрезков, на каждом из которых применяется одна из приведенных формул. Сумма полученных приближений дает приближенную формулу для вычисления интегралов по полному отрезку 
. Перейдем к выводу этих формул.
2.3. Составные квадратурные формулы
а) Формула прямоугольников
Пусть 
- равномерное разбиение отрезка 
с шагом 
, т.е. 
На каждом участке 
положим 
аппроксимируя тем самым на полном отрезке 
функцию 
кусочно-постоянной функцией (рис.2.1).
|
|
|
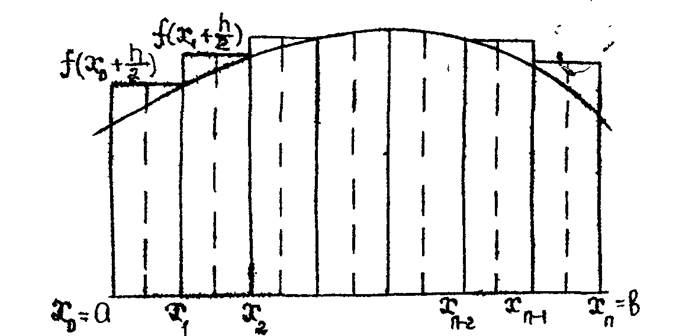
Рис.2.1. Составная формула прямоугольников
и, следовательно, в соответствии с формулой прямоугольников для каждого отрезка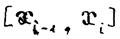 
(2.8)
(2.8) называется составной формулой прямоугольников для вычисления интеграла на полном отрезке 
Выясним погрешность этой формулы. Как было установлено в п.1 (теорема 2.1), на каждом отдельном участке 
погрешность 
формулы прямоугольников (2.4) удовлетворяет неравенству
Следовательно, полная погрешность 
(2.8) удовлетворяет неравенству
Поскольку 
, то окончательно
(2.9)
Таким образом, формула прямоугольников (2.8) имеет погрешность порядка 
, т.е.
ЗАМЕЧАНИЕ
Часто на практике формула прямоугольников используется в следующем виде
б) Формула трапеций
В этом случае на участке 
функцию 
аппроксимируем линейной функцией
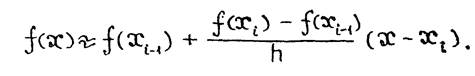
Тогда в соответствии с формулой трапеций (2.5) для участка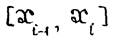 
имеем
Суммируя эти приближения, получаем составную формулу трапеций
Как и формула прямоугольников, эта формула имеет порядок точности 
; ее погрешность 
оценивается неравенством
(2.10)
Вывод этого неравенства точно такой же, как и (2.9).
в) Формула Симпсона
Разобьем отрезок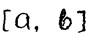 
на четное число 
частей 
На каждой паре участков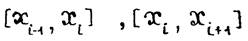 
Функцию 
аппроксимируем полиномом Лагранжа второго порядка. Тогда в соответствии с формулой Симпсона (2.6) для участков 
имеем
Суммируя формулу по всем 
получаем формулу Симпсона для полного отрезка 
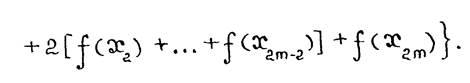(2.II)
Формула (2.11) имеет, как это следует из теоремы 2.1, порядок точности 
. Подсчет ее погрешности 
приводит к неравенству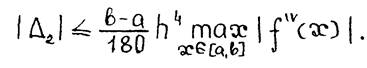 
(2.12)
Блок-схема алгоритма вычисления интегралов по формуле прямоугольников приведена на рис.2.2.
Рис.2.2. Блок-схема вычислений по формуле прямоугольников
2.4. Правило Рунге оценки погрешности
Как вытекает из (2.9) и (2.10), оценки погрешностей формул прямоугольников и трапеций требуют для своего применения вычисления вторых производных функции F(x).
Оценка (2.12) для формулы Симпсона требует производных четвертого порядка. Поскольку в практических расчетах часто функция достаточно сложна или задана таблично, вычисление производных становится труднопреодолимым препятствием. Поэтому на практике применяет теоретически не строгое, но достаточно простое правило Рунге. Оно состоит в следующем.
|
|
|
Допустим, что при подсчете интеграла 
с шагом 
погрешность счета имеет вид 
, где постоянные 
и 
не зависят от 
. Иными словами, если через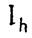 
обозначить приближенное значение интеграла 
при счете с шагом 
, то
(2.13)
Произведем теперь пересчет интеграла 
с удвоенным шагом 
. В силу нашего допущения
(2.14)
Сравнивая (2.13) и (2.14), видим, что
т.е.
Отсюда
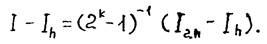
Поскольку в процессе счета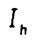 
и 
известны, это дает оценку погрешности
В частности, для формулы Симпсона
и, следовательно,
В заключение заметим, что правило Рунге называют также правилом двойного пересчета.
2.5. Компьютерная реализация методов приближенного вычисления интегралов
Для реализации на ЭВМ методов приближенного вычисления интегралов обычно применяется два способа.
Первый способ предполагает задание подынтегральной функциональной зависимости 
в виде подпрограммы пользователя. Он может быть рекомендован в случае аналитического задания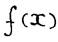 
в виде некоторого алгебраического выражения.
Второй способ предполагает задание подынтегральной функции в виде таблицы, значения которой предварительно рассчитаны.
2.6. Общая формулировка задания для практической реализации методов приближенного вычисления интегралов
Необходимо реализовать вычислительный эксперимент по расчету значений определенного интеграла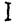 
(см. п. 2.7) рассмотренными выше методами. Целью эксперимента является получение экспериментальных данных, отражающих зависимость относительных погрешностей (2.13) от выбранного числа 
количества участков разбиения интервала интегрирования.
(2.13)
где 
- точное значение интеграла,
- приближенное значение интеграла, рассчитанное по формуле прямоугольников 
, по формуле трапеций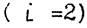 
, по формуле Симпсона 
.
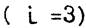Расчеты производятся 2 раза – с разбиением интервала интегрирования на N и 2N участков.
2.7. Задание
Вычислительный эксперимент производить для определенного интеграла 
. Значения a, b, N и подынтегральную функцию f(x) необходимо выбрать самостоятельно. Точное значение интеграла должно быть получено заранее для тестирования программы. Значение N выбирать из диапазона [10, 100].
|
|
|
2.8 Вопросы для контроля и самоконтроля
þ - Методы хранения целых и вещественных чисел в оперативной памяти ЭВМ.
þ - Основные квадратурные формулы. Графическая интерпретация основных приближенных методов численного интегрирования.
þ - Качественная зависимость относительной погрешности определения численного значения интеграла от шага разбиения интервала интегрирования.
þ - Опишите основные правила взаимодействия между программными единицами (основной и вспомогательной программами).
þ - Организация главной и вспомогательных программных единиц в разработанной программе выполнения вычислительного эксперимента.
þ - Структура, состав программных единиц, их назначение и формальное описание.
þ - Анализ полученных данных.
þ - Основные особенности использованных численных методов. Способы их программной реализации.
þ Что такое стиль программирования. Приведите примеры правил, определяющих стиль программирования.
þ В чем проявляется стиль программирования в реализованной вами программе.
|
|
|
