 |
1) Модель симетричного двійкового каналу.
|
|
|
|
1) Модель симетричного двійкового каналу.
| x1 |
| x2 |
| y1 |
| y2 |
| 1 - p |
| 1 - p |
| p |
| Рис. 3. Граф переходів симетричного двійкового каналу |
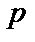 , правильного прийому), якщо швидкість маніпуляції дорівнює
, правильного прийому), якщо швидкість маніпуляції дорівнює  .
.
Рішення.
Пропускна спроможність 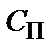 дискретного каналу при наявності завад дорівнює
дискретного каналу при наявності завад дорівнює
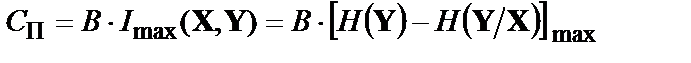 .
.
Статистика перекручувань у каналі зв'язку (рис. 2) задана відповідними умовними імовірностями 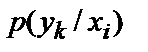 (
(  при
при 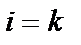 і
і 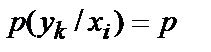 при
при  ;
;  ). Для максимізації
). Для максимізації 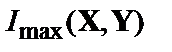 необхідно максимізувати ентропію
необхідно максимізувати ентропію 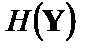 , що забезпечується при рівноймовірності передачі символів
, що забезпечується при рівноймовірності передачі символів 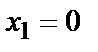 і
і 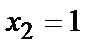 , тобто при
, тобто при 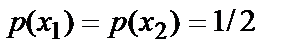 . Очевидно, що в цьому випадку справедлива рівність
. Очевидно, що в цьому випадку справедлива рівність 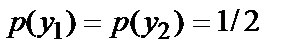 . Тоді очевидно, що
. Тоді очевидно, що
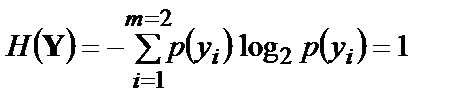 .
.
Таким чином для симетричного двійкового каналу з гаусівським шумом, тобто каналу, у якому імовірності перекручування символів «0» і «1» однакові, вираз для визначення пропускної спроможності здобуває вигляд
 , (9)
, (9)
де  – імовірність того, що при передачі символу
– імовірність того, що при передачі символу 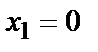 (
( 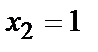 ) прийнятий символ
) прийнятий символ  (
(  ), тобто відбулося переплутування.
), тобто відбулося переплутування.
Цікаво відзначити, що 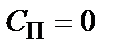 при
при 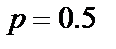 . Навіть не використовуючи канал зв'язку, значення переданого символу на прийомній стороні можна визначати шляхом ухвалення рішення за результатами підкидання монети — у 50% випадків отримаємо правильний результат. Якщо ж
. Навіть не використовуючи канал зв'язку, значення переданого символу на прийомній стороні можна визначати шляхом ухвалення рішення за результатами підкидання монети — у 50% випадків отримаємо правильний результат. Якщо ж 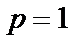 (як і у випадку
(як і у випадку  ) пропускна спроможність двійкового каналу максимальна. Це пояснюється тим, що під дією завад (шумів) усі передані символи в каналі змінюються на зворотні, тому для вірного прийому досить інвертувати всі прийняті символи.
) пропускна спроможність двійкового каналу максимальна. Це пояснюється тим, що під дією завад (шумів) усі передані символи в каналі змінюються на зворотні, тому для вірного прийому досить інвертувати всі прийняті символи.
|
|
|
Кількість інформації, що міститься в повідомленні, зростає зі збільшенням числа можливих станів рівня сигналу (для двійкових каналів їх два — «0» і «1»). З цього погляду більш вигідно застосовувати коди з основою більше двох. Однак збільшення числа рівнів сигналу обмежується впливом завад і апаратурних погрішностей (похибок, помилок).
Чим вище частота несучого періодичного сигналу, тим більше інформації в одиницю часу передається по лінії і тим вище пропускна спроможність лінії при фіксованому способі фізичного кодування. Однак, з іншого боку, зі збільшенням частоти періодичного несучого сигналу збільшується і ширина спектра цього сигналу, тобто різниця між максимальною і мінімальною частотами того набору синусоїд, що у сумі дадуть обрану для фізичного кодування послідовність сигналів. Лінія передає цей спектр синусоїд з тими перекручуваннями, що визначаються її смугою пропускання. Чим більше невідповідність між смугою пропускання лінії і шириною спектра переданих інформаційних сигналів, тим більше сигнали спотворюються і тим імовірніші помилки в розпізнаванні інформації приймаючою стороною, а значить, швидкість передачі інформації насправді виявляється меншою, ніж можна було припустити.
Зв'язок між смугою пропускання лінії (дискретного гауссового каналу зв'язку) і її максимально можливою пропускною спроможністю, поза залежністю від прийнятого способу фізичного кодування, встановив Клод Шеннон:
 , (10)
, (10)
де 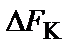 – ширина смуги пропускання лінії (каналу зв'язку);
– ширина смуги пропускання лінії (каналу зв'язку);
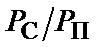 — енергетичне відношення сигнал / завада (С/П);
— енергетичне відношення сигнал / завада (С/П);
 і
і  – середні потужності сигналу і флуктуаційної завади відповідно.
– середні потужності сигналу і флуктуаційної завади відповідно.
Шеннон також показав, що в якості оцінки числа елементарних сигналів 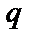 , які можуть бути використані в каналі, застосовний вираз виду
, які можуть бути використані в каналі, застосовний вираз виду
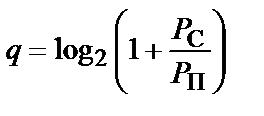 .
.
Зі (10) видно, що хоча теоретичної межі пропускної спроможності лінії з фіксованою смугою пропускання не існує, на практиці така межа є. Дійсно, підвищити пропускну спроможність лінії можна за рахунок збільшення потужності передавача або ж зменшення потужності шуму (завад) на лінії зв'язку. Обидві ці складові піддаються зміні на превелику силу. Підвищення потужності передавача веде до значного збільшення його габаритів і вартості. Зниження рівня шуму вимагає застосування спеціальних кабелів з хорошими захисними екранами, що досить дорого, а також зниження шуму в передавачі і проміжній апаратурі, чого досягти досить не просто. До того ж вплив потужностей корисного сигналу і шуму на пропускну спроможність обмежено логарифмічною залежністю, що росте далеко не так швидко, як прямо пропорційна. Так, при досить типовому вихідному відношенні потужності сигналу до потужності шуму в 100 разів підвищення потужності передавача в два рази дасть тільки 15% збільшення пропускної спроможності лінії.
|
|
|
Відповідно до (10) пропускна спроможність каналу тональної частоти із смугою пропускання  Гц і нормованим відношенням сигнал / шум 20... 30 дБ складає приблизно 20…30 Кбіт/с. Реальне значення пропускної спроможності каналів приблизно на порядок нижче. Це пояснюється тим, що формула Шеннона (10) справедлива:
Гц і нормованим відношенням сигнал / шум 20... 30 дБ складає приблизно 20…30 Кбіт/с. Реальне значення пропускної спроможності каналів приблизно на порядок нижче. Це пояснюється тим, що формула Шеннона (10) справедлива:
- для каналу з ідеальними характеристиками;
- враховує дію тільки флуктуаційних завад, тоді як на вірність передачі даних найбільший вплив роблять імпульсні завади;
- припускає оптимальне кодування, що далеко не просто здійснити практично із-за складності технічної реалізації.
|
|
|


