 |
Передаточная функция и пространство состояний
|
|
|
|
ЛЕКЦИЯ 3 МОДЕЛИ ЛИНЕЙНЫХ ОБЪЕКТОВ
Преобразование Лапласа
Одна из первых задач, которые были поставлены в теории управления – вычисление выхода системы при известном входе. Для ее решения нужно решать дифференциальные уравнения. Чтобы упростить процедуру, математики придумали преобразование, которое позволило заменить решение дифференциальных уравнений алгебраическими вычислениями, то есть, операциями с полиномами (многочленами) и рациональными функциями.
Для функции f (t) вводится преобразование Лапласа, которое обозначается как L { f (t)}
 , (13)
, (13)
Функция F (s) называется изображением для функции f (t) (оригинала). Здесь s – это комплексная переменная, которая выбирается так, чтобы интеграл (13) сходился.
Обратное преобразование Лапласа L-1 { F (s)} позволяет вычислить оригинал f (t) по известному изображению F (s)
 , (14)
, (14)
где  , а постоянная σ выбирается так, чтобы интеграл сходился.
, а постоянная σ выбирается так, чтобы интеграл сходился.
На практике вместо интеграла (14) чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот. Например, изображения по Лапласу для дельта-функции, единичного скачка и функции e − at равны, соответственно
 . (15)
. (15)
Свойства преобразования Лапласа
Преобразование Лапласа имеет несколько замечательных свойств. Во-первых, используя (13) и (14), легко доказать, что принцип суперпозиции выполняется как для прямого, так и для обратного преобразования Лапласа
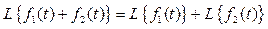 , (16)
, (16)
 . (17)
. (17)
Во-вторых, изображение для производной функции f (t) равно
 ,
,
где F (s) – изображение функции f (t), и f (0) – ее значение при t = 0. Поэтому при нулевых начальных условиях изображение производной равно изображению самой функции, умноженному на s. Аналогично для построения изображения i -ой производной нужно умножить изображение функции на si (это также справедливо только при нулевых начальных условиях).
|
|
|
Кроме того, с помощью преобразование Лапласа можно сразу найти начальное и конечное значения функции-оригинала (при t = 0 и t →∞), не вычисляя самого оригинала
 . (18)
. (18)
Передаточная Функция
Рассмотрим снова уравнение (8)
 .
.
Применим к левой и правой частям преобразование Лапласа, считая, что все начальные условия нулевые. Получается уравнение в изображениях, связывающее преобразования Лапласа входа X (s) и выхода Y (s)
 .
.
Можно вынести за скобки Y (s) в левой части и X (s) в правой части
 .
.
Разделив обе части этого равенства на  , получаем
, получаем
 . (19)
. (19)
Сравнение (12) и (19) показывает, что W (s) – это передаточная функция объекта, записанная в виде функции от комплексной переменной s, а не от оператора дифференцирования p, как в (12).
Таким образом, при нулевых начальных условиях изображение выхода линейного объекта вычисляется как произведение его передаточной функции на изображение входного сигнала.
Из (19) следует и другой важный вывод: передаточная функция равна отношению изображений по Лапласу выхода и входа при нулевых начальных условиях.
Пример
Рассмотрим пример использования преобразования Лапласа для вычисления выхода системы при известном входном сигнале. Пусть объект управления описывается уравнением первого порядка
 .
.
и на его вход поступает единичный ступенчатый сигнал x (t) = 1 (t). Требуется найти сигнал выхода y (t), который в данном случае представляет собой переходную характеристику.
Решим эту задачу с помощью передаточных функций и изображений сигналов по Лапласу. Чтобы найти изображение выхода по формуле (19), нужно знать изображение входного сигнала X (s) и передаточную функцию звена W (s). Изображение входа находим по табличным данным (см. (15)), а передаточную функцию – из заданного уравнения, повторяя приведенные выше рассуждения
|
|
|
 .
.
Теперь находим изображение выхода
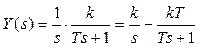 .
.
и представляем его в виде суммы элементарных дробей
 .
.
Используя принцип суперпозиции для изображений (17), вычисляем оригинал – сигнал выхода
 .
.
Обратные преобразования Лапласа находим по таблице
 при t > 0,
при t > 0,
что совпадает с (7). Таким способом можно вычислять реакцию системы на известный входной сигнал без прямого решения дифференциального уравнения.
Применяя формулы (18) для вычисления начального и конечного значений сигнала выхода y (t). При ступенчатом входном сигнале с изображением  получаем
получаем
 ,
,
Таким образом, для рассмотренного выше примера
 .
.
Значение W (0) называют статическим коэффициентом усиления звена, поскольку он показывает, во сколько раз усиливается постоянный сигнал.
Передаточная функция и пространство состояний
Используя преобразование Лапласа, можно построить передаточную функцию для модели объекта в пространстве состояний

Здесь u (t), y (t) и x (t) обозначают соответственно вход, выход и вектор состояния объекта. Преобразуя левые и правые части каждого уравнения по Лапласу (переходя к изображениям сигналов по Лапласу при нулевых начальных условиях), получаем
 . (20)
. (20)
В первом уравнении перенесем все члены, зависящие от X (s), в левую часть
 ,
,
где I обозначает единичную матрицу, у которой на главной диагонали стоят единицы, а все остальные элементы – нули. Умножая обе части последнего равенства на (s ⋅ I − A)−1, получим выражение для X (s)
 ,
,
которое при подстановке во второе уравнение в (20) дает
 .
.
Чтобы определить передаточную функцию, найдем отношение изображений выхода и входа
 . (21)
. (21)
Обратный переход, от передаточной функции к модели в пространстве состояний, более сложен и неоднозначен. Дело в том, что каждой передаточной функции соответствует бесчисленное множество моделей в пространстве состояний. Одну из них можно найти следующим образом. Для передаточной функции
 ,
,
где d, ai (i =0,1,2) и bi (i =0,1,2) – постоянные коэффициенты, модель в пространстве состояний задается матрицами
 , (22)
, (22)
При увеличении порядка передаточной функции (степени ее знаменателя), эти матрицы расширяются. В нижней строке матрицы A записываются коэффициенты знаменателя с обратным знаком, над главной диагональю – единицы, а остальные элементы – нули. В матрице B только самый последний элемент – единица, а остальные – нули. Наконец, матрица С строится из коэффициентов числителя передаточной функции.
|
|
|
Отметим, что модель, заданную неправильной передаточной функцией (у которой степень числителя больше степени знаменателя) нельзя представить в пространстве состояний.
Частотные характеристики
Еще один популярный эталонный сигнал – гармонический (синус, косинус), например
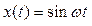 , (23)
, (23)
где ω – угловая частота (в радианах в секунду). Можно показать, что при таком входе на выходе линейной системы в установившемся режиме (при больших t) будет синус той же частоты, но с другой амплитудой A и сдвигом фазы φ
 .
.
Для каждой частоты входного сигнала будет своя амплитуда и свой сдвиг фазы. Чтобы определить по графику фазовый сдвиг φ, нужно найти расстояние Δ t по оси времени между соответствующими точками синусоид (например, точками пересечения с осью t или вершинами). Если Δ t умножить на частоту ω, получаем сдвиг фазы φ (в радианах).

На рисунке показан случай φ > 0 (опережение по фазе), когда выход сдвинут «влево» по оси времени относительно входа, то есть, «идет раньше» входного. Зная передаточную функцию системы W (s), можно вычислить амплитуду и сдвиг фазы по формулам
 .
.
Для каждой частоты ω значение  – это некоторое комплексное число, имеющее амплитуду
– это некоторое комплексное число, имеющее амплитуду  и фазу
и фазу  .
.
Функция W (jω) называется частотной характеристикой звена, поскольку она характеризует выход системы при гармонических сигналах разной частоты. Зависимости P (ω) и Q (ω) (вещественная и мнимая части W (j ω)) – это вещественная и мнимая частотные характеристики.
Функции A (ω) и φ (ω) (они для каждой частоты принимают вещественные значения) называются соответственно амплитудной и фазовой частотными характеристиками (АЧХ и ФЧХ). Амплитудная частотная характеристика – это коэффициент усиления гармонического сигнала. Если на какой-то частоте ω значение A (ω) > 1, входной сигнал усиливается, если A (ω) < 1, то вход данной частоты ослабляется.
|
|
|
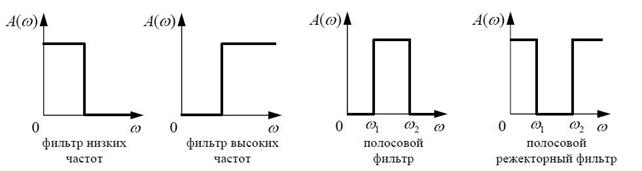
По форме АЧХ различают несколько основных типов звеньев:
1) фильтр низких частот – пропускает низкочастотные сигналы примерно с одинаковым коэффициентом усиления, блокирует высокочастотные шумы и помехи;
2) фильтр высоких частот – пропускает высокочастотные сигналы, блокирует сигналы низкой частоты;
3) полосовой фильтр – пропускает только сигналы с частотами в полосе от ω1 до ω2;
4) полосовой режекторный фильтр – блокирует только сигналы с частотами в полосе от ω1 до ω2, остальные пропускает.
На рисунке показаны амплитудные частотные характеристики идеальных фильтров этих четырех типов.
В радиотехнике используется понятие полосы пропускания – это ширина полосы частот, в которой значение АЧХ больше, чем 1/ 2 от ее максимального значения.
Частотные характеристики во многих случаях можно снять экспериментально. Если объект устойчивый, на его вход подается гармонический сигнал (23) и записывается сигнал y (t) на выходе. Определив амплитуду и сдвиг фазы для разных частот, можно построить по точкам амплитудную и фазовую частотные характеристики.
Если объект неустойчив, то при подаче на вход синуса амплитуда колебаний на выходе будет неограниченно расти. Однако частотную характеристику все равно можно определить экспериментально. Для этого нужно сначала найти какой-нибудь регулятор, который сделает замкнутую систему устойчивой. Затем на вход r (t) подают синусоидальный сигнал и сравнивают сигналы x (t) и y (t) на входе и выходе интересующего нас объекта, определяя для каждой частоты ω «коэффициент усиления» A (ω) (отношение амплитуд сигналов x (t) и y (t)) и сдвиг фазы φ (ω).

|
|
|


