|
| Больший корень уравнения принадлежит промежутку 2х2 – 3х – 2 = 0.
А)[-6;2), B)(2;0) C)(-∞;-4] D)[0;4] E)(-4;1)
|
| Найдите удвоенное произведение корней уравнения
x2-8x+15=0
|
|
| Вычислите 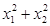 , если х1,х2 различные решения уравнения , если х1,х2 различные решения уравнения 
|
| Найдите удвоенную сумму корней уравнения:
х2 -7х + 12 = 0.
|
|
| Вычислить 8  где где 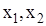 - корни уравнения 9 - корни уравнения 9 
|
| Не вычисляя корней 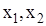 уравнения 2х2+5х-3=0. Найдите уравнения 2х2+5х-3=0. Найдите 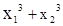
|
|
| Вычислить 8  где где 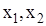 - корни уравнения 9 - корни уравнения 9 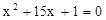
|
| Не вычисляя корней х1 и х2 уравнения 2x2 + 5х - 3 = 0. Найдите: х 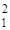 + х + х 
|
|
| Вычислить  , где , где  и и  корни уравнения корни уравнения  . .
|
| Не вычисляя корней х1 и х2 уравнения 2х2 + 5х – 3 = 0, найти (х1 + х2) + (х1.х2).
|
|
| Дано уравнение х2 + kх + 34 = 0, где х1 и х2 – корни уравнения. Найти k, если х2- х1=  , а корни положительные (х2> х1) , а корни положительные (х2> х1)
|
| Не вычисляя корней х1 и х2 уравнения
2x2 -3х - 4 = 0. Найдите: х 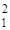 + х + х 
|
|
| Дано уравнение  , где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2 , где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2 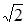 , а корни положительны. , а корни положительны.
|
| Один из корней уравнения х2 + х –а = 0 равен (-3) при а равном:
|
|
| Дано уравнение  , где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2 , где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2  , а корни положительны (х2> х1). , а корни положительны (х2> х1).
|
| Один из корней уравнения х2+px-10=0 равен 1 при р равном
|
|
| Дано уравнение х2 + 7х + 1 = 0. Найти сумму квадратов его корней
|
| Один из корней уравнения х2 +рх +10 = 0 равен
(-1) при р равном:
|
|
| Дано уравнение  .
Найти (х1+х2)+(х1х2) .
Найти (х1+х2)+(х1х2)
|
| Один из корней уравнения х2+px-35=0 равен 7. Найдите другой корень уравнения.
|
|
| Дано уравнение  . Найти . Найти 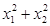
|
| Один из корней уравнения х2+px-16=0 равен -1. Найдите другой корень уравнения.
|
|
| Дано уравнение 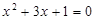 . Найти сумму кубов его корней.. . Найти сумму кубов его корней..
|
| Один из корней уравнения х2-x+q=0 равен 5. Найдите другой корень уравнения.
|
|
| Дискриминант какого из уравнений равен 25
А) 4х2-3х+1=0 В) 2х2-3х+2=0 С) 2х2+3х-2=0
D)х2+3х+25=0 Е) 4х2-х-4=0
|
| Определить нули функции у = 12-7х+х2
|
|
| Дискриминант какого из уравнений равен 49
А) 5х2+3х+2=0 В) 2х2-3х-5=0 С) 3х2-3х-7=0
D) 2х2-3х+5=0 Е) 5х2-3х+2=0
|
| При каких значениях у верно равенство
(2у-3)2=у2+4у+4
|
|
| Если корни квадратного уравнения  удовлетворяют условию удовлетворяют условию  , тогда q равно: , тогда q равно:
|
| Приведенное квадратное уравнение, в котором коэффициент при х равен (-1), а один из корней больше другого на 3, имеет вид
|
|
| Если корни квадратного уравнения  удовлетворяют условию удовлетворяют условию 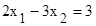 , тогда q равно (х1<x2): , тогда q равно (х1<x2):
|
| Приведённое квадратное уравнение, в котором коэффициент при х = (-5), а один из корней больше другого на 1, имеет вид:
|
|
| Если корни квадратного уравнения х2 +рх - 16 = 0 удовлетворяют условию  , тогда положительное значение , тогда положительное значение 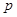 равно: равно:
|
| Какое решение уравнения правильно?
1. х2 – 16 = 0, х = 4
2. х2 – х + 5 = 0, х = 2, х = -1.
3. х2 – 2х + 1 = 0, х = 1, х = -1.
4. х2 – 4х + 3 = 0, х = 3, х = 1 – прав.
|
|
| Если корни квадратного уравнения х2 + рх – 16 = 0 удовлетворяют условию  , тогда отрицательное значение , тогда отрицательное значение 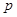 равно: равно:
|
| При каких значениях х верно равенство
(3х+1)2=3х+1
|
|
| Какие из данных уравнений не имеют корней:
1) -х2+3х=0 2) 2х2+х+7=0 3) 3х4+х2+1=0 4) х2-х-7=0
|
| При каких значениях х выполняется равенство:
х2 – х = 0?
|
|
| Какая из пар чисел удовлетворяет уравнению:
20х2+у2-4ху+24х+9=0
А)(4;3); В)( ); С)(-4;-3); D)( ); С)(-4;-3); D)( ); Е(5;6) ); Е(5;6)
|
| Какие из уравнений являются равносильными на множестве R?
1. 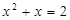 . 2. . 2.  . 3. . 3.  . 4. . 4.  . .
|
|
| При каких значениях х справедливо равенство:
х(х – 2) = 0?
|
| При каких значениях n уравнение х2+nx-3n=0 имеет вещественные корни?
|
|
| При каких значениях многочлены (2-х)(2х+1) и
(х-2)(х+2) равны
|
| При каком значении а (а≠0) квадратный трехчлен
ах2-4х+2 имеет два корня?
|
|
| Квадратное уравнение, корни которого равны  и и 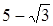 , имеет вид: , имеет вид:
|
| При каких значениях m уравнение 3х2+2х+m=0 имеет один корень?
|
|
| Квадратное уравнение, корни которого равны  и и 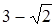 , имеет вид: , имеет вид:
|
| При каких значениях  уравнение уравнение  имеет один корень? имеет один корень?
|
|
| Корни уравнения х2 – 4х + 3 = 0 принадлежат промежутку:
|
| При каких значениях  уравнение уравнение 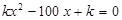 имеет один корень? имеет один корень?
|
|
| Корни уравнения 7х2 – х – 8 = 0 принадлежат промежутку:
|
| При каких значениях  уравнение уравнение  имеет один корень? имеет один корень?
|
|
| Корни уравнения 2х2 – 50 = 0 принадлежат промежутку:
|
| Произведение корней уравнения f(x)=f(-1),
где f(x)=2x2-5x+1 равно
|
|
| Меньший корень уравнения 2х2 -3х – 2 = 0 принадлежит промежутку:
|
| Произведение корней уравнения 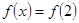 ,
где ,
где 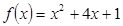 , равно: , равно:
|
|
| Наибольшее целое значение 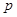 , при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно: , при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно:
|
| Произведение корней уравнения 6х2 + х – 7 = 0 равно:
|
|
| Наименьшее целое значение 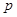 , при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно: , при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно:
|
| Произведение корней уравнения 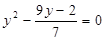 равно: равно:
|
|
| Найдите больший корень уравнения х2 + 9х – 10 = 0
|
| Разность корней уравнения х2-12х+g=0 равна 2. Найдите g.
|
|
| Найдите меньший корень уравнения 2х2+7х-9=0
|
| Решите уравнение 3х2+5х=0, в ответе указать сумму корней.
|
|
| Найдите произведение корней уравнения:
х2 + 7х – 8 = 0.
|
| Составьте квадратное уравнение по его корням:
4-  и 4+ и 4+ 
|
|
| Найдите произведение корней уравнения:
х2 – 2х – 3 = 0
|
| Составить приведенное квадратное уравнение имеющее корни х1=2а-b, х2= a-2b
|
|
| Найти сумму корней уравнения: 
|
| Составить приведённое квадратное уравнение, имеющее корни х1 = 3, х2 = -1.
|
|
| Найти сумму корней уравнения: 
|
| Составить приведённое квадратное уравнение, имеющее корни 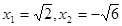 . .
|
|
| Найдите сумму корней уравнения: х2 + 5х – 6 = 0
|
| Составить приведенное квадратное уравнение имеющее корни х1=3, х2=-1
|
|
| Найти сумму корней уравнения 3х2 – 4х – 2 = 0
|
| Составить приведенное квадратное уравнение имеющее корни х1=  , х2=- , х2=- 
|
|
| Найдите сумму квадратов корней уравнения
 -12х + 35 = 0. -12х + 35 = 0.
|
| Сумма корней уравнения 6х2+х-7=0 равна:
|
|
| Найдите сумму квадратов корней уравнения
 + 3х – 15 = 0. + 3х – 15 = 0.
|
| Сумма корней уравнения  равна: равна:
|
|
| Найдите сумму квадратов корней уравнения 3  - 5х – 2 = 0. - 5х – 2 = 0.
|
| Уравнение 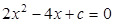 имеет два действительных различных корня, если: имеет два действительных различных корня, если:
|
|
| Найдите сумму корней уравнения 3  + 5х – 8 = 0. + 5х – 8 = 0.
|
| Уравнение 2х2 – 4х + с = 0 не имеет действительных корней, если:
|
|
| Найдите сумму корней уравнения: 3х2 – 5х – 2 = 0
|
| Уравнение  имеет единственный корень при с равном: имеет единственный корень при с равном:
|
|
| Найдите сумму кубов корней уравнения:
х2 + 3х- 15 = 0.
|
| Уравнение  имеет единственный корень при m равном: имеет единственный корень при m равном:
|
|
| Найдите число (-13х+2)2+х, где х – корень уравнения 
|
| Является ли решением уравнения х2 –у = -2 пара значений переменных:
х = 1; у = 3..
|
|
| Найдите число в два раза большее меньшего корня уравнения: х2 – 5х + 6 = 0.
|
|
|


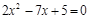

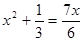







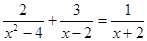
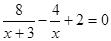









 = 5.
= 5.
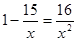


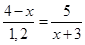

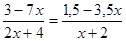

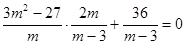


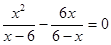
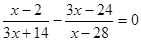


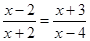

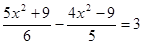

















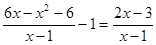






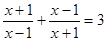

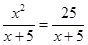




 принадлежит промежутку
А)[-6;1], B)(-4;0) C)(-∞;-4] D)[0;4] E)(-4;1)
принадлежит промежутку
А)[-6;1], B)(-4;0) C)(-∞;-4] D)[0;4] E)(-4;1)
 = 4
= 4

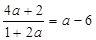

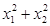 , если х1,х2 различные решения уравнения
, если х1,х2 различные решения уравнения 
 где
где 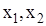 - корни уравнения 9
- корни уравнения 9 
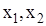 уравнения 2х2+5х-3=0. Найдите
уравнения 2х2+5х-3=0. Найдите 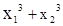
 где
где 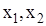 - корни уравнения 9
- корни уравнения 9 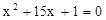
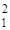 + х
+ х 
 , где
, где  и
и  корни уравнения
корни уравнения  .
.
 , а корни положительные (х2> х1)
, а корни положительные (х2> х1)
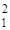 + х
+ х 
 , где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2
, где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2 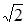 , а корни положительны.
, а корни положительны.
 , где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2
, где x1 и x2 - корни уравнения. Найти p, если x2 – x1= 2  , а корни положительны (х2> х1).
, а корни положительны (х2> х1).
 .
Найти (х1+х2)+(х1х2)
.
Найти (х1+х2)+(х1х2)
 . Найти
. Найти 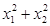
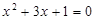 . Найти сумму кубов его корней..
. Найти сумму кубов его корней..
 удовлетворяют условию
удовлетворяют условию  , тогда q равно:
, тогда q равно:
 удовлетворяют условию
удовлетворяют условию 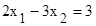 , тогда q равно (х1<x2):
, тогда q равно (х1<x2):
 , тогда положительное значение
, тогда положительное значение 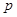 равно:
равно:
 , тогда отрицательное значение
, тогда отрицательное значение 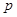 равно:
равно:
 ); С)(-4;-3); D)(
); С)(-4;-3); D)( ); Е(5;6)
); Е(5;6)
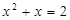 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.
 и
и 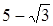 , имеет вид:
, имеет вид:
 и
и 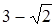 , имеет вид:
, имеет вид:
 уравнение
уравнение  имеет один корень?
имеет один корень?
 уравнение
уравнение 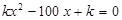 имеет один корень?
имеет один корень?
 уравнение
уравнение  имеет один корень?
имеет один корень?
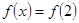 ,
где
,
где 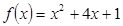 , равно:
, равно:
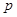 , при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно:
, при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно:
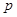 , при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно:
, при котором уравнение х2 – рх + 9 = 0 не имеет действительных корней, равно:
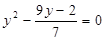 равно:
равно:
 и 4+
и 4+ 


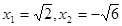 .
.
 , х2=-
, х2=- 
 -12х + 35 = 0.
-12х + 35 = 0.
 + 3х – 15 = 0.
+ 3х – 15 = 0.
 равна:
равна:
 - 5х – 2 = 0.
- 5х – 2 = 0.
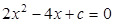 имеет два действительных различных корня, если:
имеет два действительных различных корня, если:
 + 5х – 8 = 0.
+ 5х – 8 = 0.
 имеет единственный корень при с равном:
имеет единственный корень при с равном:
 имеет единственный корень при m равном:
имеет единственный корень при m равном:





