 |
Глава 2 логика рефлексивных игр
|
|
|
|
Имитация решений
Наша задача теперь показать, что выработка решения конфликтующими сторонами сводится к построению рефлексивной проекции ситуации, охватывающей и «проецирующие» органы сторон.
Формальная логика не выделила специфику рассуждений в конфликте. Основываясь на понятиях «истинности» и «ложности», формальная логика позволяет определить, кто из спорящих прав, анализируя только их рассуждения без обращения к той действительности, по отношению к которой эти рассуждения строятся. Логика рефлексивных игр иная. Понятия «истинности» и «ложности» не могут служить ее фундаментом. Конфликтность ситуации проявляется в особом характере рассуждений, и в отличие от научного спора в конфликте побеждает наиболее изощренный лжец.
Для описания логики рефлексивных игр воспользуемся тем основным фактом, что конфликтующие стороны воспроизводят рассуждения друг друга.
Обозначим игроков через X и Y. Пусть  означает «X думает» и
означает «X думает» и  —.«Y думает». Если X может имитировать рассуждение Y или, что то же самое, если его ранг рефлексии выше, то это можно записать как
—.«Y думает». Если X может имитировать рассуждение Y или, что то же самое, если его ранг рефлексии выше, то это можно записать как  — «X думает, что Y думает» (стрелка означает порядок чтения). Если же У может проимитировать X, который воспроизводит рассуждение У, то, очевидно, это может быть записано следующим образом:
— «X думает, что Y думает» (стрелка означает порядок чтения). Если же У может проимитировать X, который воспроизводит рассуждение У, то, очевидно, это может быть записано следующим образом:
 — «У думает, что X думает, что Y думает».
— «У думает, что X думает, что Y думает».
Понятно, что такая цепочка может быть продолжена влево и символ, стоящий первым справа, указывает на потенциального победителя.
Предложенный здесь способ записи является наиболее общим и наиболее простым для описания самого факта рефлексии. Когда шахматист X ставит ловушку партнеру Y, основанную на том, что X знает, как Y представляет себе ход мысли X, то это просто записывается как 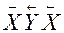 . Долгую борьбу Порфирия Петровича с Раскольниковым, всю построенную на лжи и на уверенности, что противник понимает,
. Долгую борьбу Порфирия Петровича с Раскольниковым, всю построенную на лжи и на уверенности, что противник понимает,
|
|
|
Конец страницы 20
¯ Начало страницы 21 ¯
что это ложь, вероятно, тоже можно изобразить подобным же образом —  . Однако это не слишком удобно и недостаточно для нашей главной цели: описать процесс принятия решения. Поэтому попробуем иначе изобразить рефлексивное взаимодействие сторон.
. Однако это не слишком удобно и недостаточно для нашей главной цели: описать процесс принятия решения. Поэтому попробуем иначе изобразить рефлексивное взаимодействие сторон.
Рассмотрим исходную ситуацию, когда противники принимают решения, не имитируя рассуждения друг друга. Этот вырожденный случай, когда ранги рефлексии равны нулю, нам понадобился, чтобы описать простейшую процедуру принятия решения.
Представим себе объективную обстановку как некоторый плацдарм, на котором развертываются события и который обозначим буквой П. Пусть это будет, например, несколько населенных пунктов, в которые игроку X требуется завезти грузы одним рейсом грузовика, то есть перед X стоит задача выбора оптимального маршрута. Плацдарм П отображается, допустим, на особый планшет, которым владеет X. Обозначим этот планшет Пх. Очевидно, что отображение плацдарма П может быть произведено с различной точностью. Например, некоторые пункты могут быть пропущены, их расположение может быть искажено и т. д. Но X оперирует с Пх, а не с П; это надо запомнить, потому что решение, которое он примет, будет соотнесено с Пх и лишь затем с большим или меньшим успехом переведено на реальный плацдарм П.
Игрок X имеет цель — Цх. В нашем примере цель состоит в том, чтобы перевезти грузы из исходного пункта А во все другие пункты одним грузовиком с минимальной затратой времени или горючего. Чтобы принять решение, в результате которого цель будет достигнута, X должен произвести, определенные операции на своем планшете.
Предположим, что X владеет каким-либо методом решения задачи, например методом линейного программирования. Этот метод мы назовем доктриной и обозначим Дх. Используя Дх, игрок X находит кратчайший маршрут, проходящий через каждый пункт не более одного раза. Этот маршрут наносится на планшет Пх и является решением задачи — Рх.
|
|
|
Процедура принятия решения игроком X может быть изображена следующим образом:
1) Реальная обстановка «переводится» на планшет Пх.
2) Цель особым образом соотносится с планшетом; несколько огрубляя суть дела, можно сказать, что цель «наносится» на планшет:

3) К планшету с нанесенной на него целью применяется доктрина

Конец страницы 21
¯ Начало страницы 22 ¯
4) В результате этой операции вырабатывается решение, отнесенное к планшету Пх:

Выражение (1) является весьма общим, и по описанной Схеме принимаются решения в самых разнообразных конфликтных ситуациях, когда игроки не имитируют рассуждений друг друга.
Возвратимся теперь к противнику — игроку Y и рассмотрим процесс принятия решения, когда У может имитировать решение X, то есть к схеме  . В нашем примере Y желает овладеть грузовиком, который перевозит грузы X, и должен организовать засаду. Засада может быть организована лишь в окрестностях узлового пункта К, так как только он находится в лесу. Однако для этого Y необходимо знать, с какой стороны в К будет следовать грузовик. Никакой информации о выбранном X маршруте у У нет. Для того чтобы принять решение, обеспечивающее успех, Y должен проимитировать рассуждение X и должен проделать процедуру (1).
. В нашем примере Y желает овладеть грузовиком, который перевозит грузы X, и должен организовать засаду. Засада может быть организована лишь в окрестностях узлового пункта К, так как только он находится в лесу. Однако для этого Y необходимо знать, с какой стороны в К будет следовать грузовик. Никакой информации о выбранном X маршруте у У нет. Для того чтобы принять решение, обеспечивающее успех, Y должен проимитировать рассуждение X и должен проделать процедуру (1).
Обратим внимание на одно важное обстоятельство: Y не является обладателем Пх. Он владеет тем, что можно назвать «планшет Пх с точки зрения Y». Это уже вторичное отражение реального плацдарма и при этом, очевидно, могут появиться существенные отличия от Пх. Игрок Y не обладает также Цх и Дх; он располагает лишь «ЦХ с точки зрения Y» и «Дx с точки зрения Y». Приняв соответствующие обозначения Пху, Цху, Дxу и Рху, мы можем записать имитацию Y рассуждения X следующим образом:

Хотя плацдарм П игроком Y может отображаться иначе, чем X, и Y считает, что Пу точнее, чем Пх, имитацию процедуры (1) он проводит не со своим планшетом, а с тем, который, с его точки зрения, есть у противника. И только после р того как Y получил — 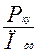 , он должен перевести это решение на свой собственный планшет Пу:
, он должен перевести это решение на свой собственный планшет Пу:
|
|
|

Теперь Y должен нанести на свой планшет свою цель, применить свою доктрину и выработать решение, которое заключается в определении точки маршрута, в которой Y устроит засаду. Изображая этот процесс в принятых обозначениях, получим:

Конец страницы 22
¯ Начало страницы 23 ¯
Объединив выражения (2), (3) и (4), запишем процесс принятия решения с имитацией по схеме XY, как

В этом примере X терпит поражение, поскольку Y удалось проимитировать рассуждения X. В частности, если бы X не стремился к оптимизации маршрута, а Y считал бы, что X, наоборот, стремится к нему, победа осталась бы за X.
Так как X не располагает Пху, Цху и Дху, а имеет «Пху с точки зрения X», «Цху с точки зрения X» и «Дху с точки зрения X», то, приняв соответствующие обозначения Пхух, Цхух и Дхух, можно записать процесс решения с двойной имитацией (по схеме  ) следующим образом:
) следующим образом:

В выражении (6) легко просматривается общий рекуррентный закон, по которому можно получать формулы для любых рангов рефлексии.
Соотношения (1) — (6) мы вывели, предполагая, что цель независима от изображения плацдарма на планшете. Во многих случаях цель определяется в результате оперирования с планшетом. Тогда выражение (1) запишется следующим образом:
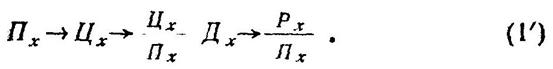
Формальный аппарат
Вообразим теперь некоего внешнего наблюдателя, на глазах у которого разворачивается рефлексивная игра. Может ли он представить себе общую картину этого конфликта? Какими средствами он должен пользоваться, чтобы «схватить» рефлексивные рассуждения игроков? Очевидно, для этой цели требуется логический аппарат, специально предназначенный для отображения рефлексивного взаимодействия и обладающий необходимой общностью.
Покажем, что незначительное развитие только что рассмотренного способа изображения имитированных решений удовлетворяет этому требованию.
Итак, наш наблюдатель видит прежде всего двух игроков X и Y и реальный плацдарм с ударными силами игроков. На этом плацдарме протекает физическое взаимодействие игро-
|
|
|
Конец страницы 23
¯ Начало страницы 24 ¯
ков — пусть это будет, например, передвижение фигур на шахматной доске.
Условимся игроков X и Y изображать в виде следующих символических сумм:
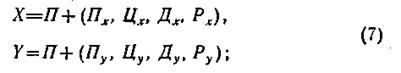
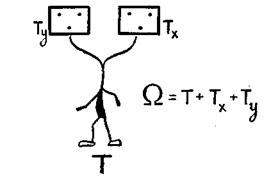
Рис. 1.
Практически бессмысленно отрывать игрока от реального плацдарма, наоборот, плацдарм П удобно представить в виде «тела» игрока, считая, что отражение тела происходит в его голове.
Обозначив П=Т, (Пх, Цх, Дх, Рx)=Тx и (Пу, Цу, Ду, Ру)=Ту, мы упростим символические суммы:

Условимся изображать конфликт в виде «двухголового человечка» (рис. 1). Этому человечку будет соответствовать следующая символическая сумма:

В головах нашего человечка отражается тело Т и результатами этого отражения являются Тх и Ту.
Теперь нетрудно сообразить, что если X имитирует рассуждения Y, то есть принимает решение по схеме  , то ему необходимо иметь еще одну голову, в которой он мог бы отразить Ту. В этом случае вся ситуация будет выглядеть так, как изображено на рис. 2.
, то ему необходимо иметь еще одну голову, в которой он мог бы отразить Ту. В этом случае вся ситуация будет выглядеть так, как изображено на рис. 2.
Конец страницы 24
¯ Начало страницы 25 ¯
Повышение рангов рефлексии влечет за собой соответствующее «наращивание» голов.
Будем полагать, что в голове каждого ранга (этажа) могут отражаться головы только предшествующего ранга, но находящиеся на обеих ветвях, то есть принадлежащие обоим игрокам. Общее правило формирования подобных рефлексивных элементов состоит в следующем: голове ранга і соответствует сумма элементов, находящихся в головах ранга і— 1, с добавленным индексом ветви.
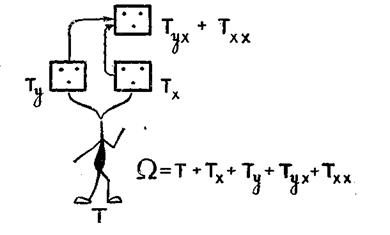
Рис. 2.
Описанный здесь механизм позволяет изображать сколь угодно сложные и запутанные рефлексивные структуры с помощью сумм типа:

где х1 = х, х2 = у, причем любое подмножество слагаемых может отсутствовать за исключением слагаемого Т.
Возникает вопрос: как следует интерпретировать элементы типа Тххх, Тухх, Тхх, то есть те, в которых один индекс встречается два и более раз подряд в конце последовательности индексов? Эти элементы можно интерпретировать как управляющие процессом отражения на нижележащем уровне. В Тхх вырабатываются решения, которые реализуются в Т х. Мы видели выше, что в Тх вырабатываются решения, реализуемые на реальном плацдарме. Рассматривая рис. 2, мы можем заметить, что сумма Тух + Тхх легко интерпретируется как осознание суммы элементов Ту + Тх. Отсюда, естественно, вы-
Конец страницы 25
¯ Начало страницы 26 ¯
текает закон дистрибутивности относительно правого индекса:

Слагаемые в выражении (9) могут быть сгруппированы различным образом.
|
|
|
В настоящее время трудно указать формальные схемы процедур принятия решения для более сложных случаев, чем

Однако принципиально возможно представить любого игрока в виде суммы рефлексивных элементов и привести эту сумму в соответствии с правилами этой своеобразной алгебры к виду, удобному для анализа. Это позволяет характеризовать по существу те решения, которые должны быть приняты в результате оперирования этими элементами.
Первой и самой простой операцией над суммами вида (9) является операция выделения оснований для принятия решений. Пусть игрок X изображен в виде суммы

Все, что находится в скобках, осознано игроком X, и чтобы представить его внутреннюю картину, мы должны выделить
Т+Ту+Тху.
Это достигается следующей операцией над выражением (12):
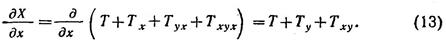
Заметим, что мы пользуемся чисто внешними аналогиями, употребляя символику математического анализа. Просто те алгебраические операции, которые связаны с описанием рефлексивных процессов, напоминают формулы интегрирования и дифференцирования многочленов. Никакого «количественного» смысла эта символика не имеет.
Выражение (13) представляет собой символическую запись игрока Y с точки зрения X. Это выражение таким же образом может быть «продифференцировано» и могут быть получены основания, которыми пользовался Y при принятии решения (с точки зрения X).
Так как
Т+Ту + Тху = Т+(Т+Тх)у.
получаем:

Конец страницы 26
¯ Начало страницы 27 ¯
С позиции внешнего исследователя, выражение (14) может быть интерпретировано как основание для принятия решения игроком Y с точки зрения X:
(Т+Тх)ух. (15)
Мы представили конфликт в виде символического многочлена Ω. Условимся теперь, что вместо членов вида Тххх или Тххуу будем писать  и ТХ2У2. Заметим, что в нашей алгебре «умножение» не коммутативно, то есть Тху ≠ Tx. Действительно, левый элемент интерпретируется как Тх с точки зрения Y, а правый элемент — как Ту с точки зрения X, и смысл, вкладываемый в эти члены, различен. Есть еще одно существенное отличие этой алгебры от «обычной». Одно слагаемое может быть повторено произвольное число раз, например,
и ТХ2У2. Заметим, что в нашей алгебре «умножение» не коммутативно, то есть Тху ≠ Tx. Действительно, левый элемент интерпретируется как Тх с точки зрения Y, а правый элемент — как Ту с точки зрения X, и смысл, вкладываемый в эти члены, различен. Есть еще одно существенное отличие этой алгебры от «обычной». Одно слагаемое может быть повторено произвольное число раз, например,
Т+ Тх + Тх + Тх = Т+ Тх
Это правило естественно, так как при репродуцировании какого-либо «текста» не возникает новой информации. Безразлично, чем располагает игрок — одним элементом Тх или тремя.
Любую сумму, изображающую рефлексивное взаимодействие двух игроков, с позиции внешнего исследователя можно представить в виде

где Ω' и Ω" — некоторые суммы, выражающие соответственно основания решений игрока X и игрока Y. Общее правило выявления оснований таково:

С помощью этих операций исследователь как бы извлекает или заимствует картины, лежащие перед игроками.
В общем случае многочлены Ω' и Ω" могут быть приведены к виду (16) и в свою очередь подвергнуты операции дифференцирования. Вторые производные и производные более высоких порядков определяются аналогично правилу (17).
Это правило легко обобщается и переносится на случай многих игроков. Рассмотрим, например, ситуацию взаимного отражения, в которой действуют пять игроков: а1, а2, аз, а4 и a5 и которая может быть представлена; как сумма, записанная в произвольном порядке

Конец страницы 27
¯ Начало страницы 28 ¯
Изобразив так картину рефлексивного взаимодействия, мы можем ставить разные задачи. Например, мы можем узнать, как с точки зрения а5 игроки а4 и а3 представляют себе а5. Продифференцируем Q по а5. Члены, имеющие крайний правый индекс, отличный от а5, исчезнут, а у членов с крайним индексом а5нужно его зачеркнуть:

Найдем точки зрения а4 и а3, Для этого продифференцируем (18) по а4 и а3:

Выделим члены, принадлежащие as. Получим:
Ta2,as — это игрок as, как он представляется а4 с точки зрения as.
Т a2а4а5 — это игрок а5, как он представляется аз с точки зрения as.
Взаимные многократные отражения в большом коллективе могут порождать очень сложные суммы. Последовательным дифференцированием по различным основаниям мы можем извлекать произвольные картины, лежащие в более сложных картинах и т. д.
Основной процедурой в процессе принятия решения является осознание ситуации. Что скрывается за этим термином? Интуитивно чувствуется, что осознание с операциональной стороны это резкий переход, скачок: то, что do было скрыто, после оказывается перед глазами. Мы будем полагать, что осознанием является отражение одним из игроков всей системы Ω в некоторый момент времени. Рассмотрим систему:
Ωi = Xi + Yi
(і — здесь и далее некоторый момент времени). Пусть в момент i+1 X произвел осознание, то есть отразил всю систему такой, какой она была в момент і. В результате система Ω внешнему наблюдателю представится как

Игрок Y не производил осознания, поэтому он без изменения «перешел» в следующий момент времени. Операцию осознания мы будем обозначать как нахождение символической первообразной:

или, опуская индексы,

Конец страницы 28
¯ Начало страницы 29 ¯
В отличие от математического анализа мы не употребляем значок дифференциала, а роль константы, появляющейся после «интегрирования», выполняет Y.
Теперь нетрудно увидеть, что основание, которое лежит перед игроком X в момент і+l, тождественно состоянию системы Ω в момент і. Поэтому операцию дифференцирования можно истолковать не только как выделение оснований для принятия решения, но и как переход от Ωi+1 к Ωi.

Рис. 3.
Процедура осознания ситуации другим игроком фиксируется аналогичным выражением:
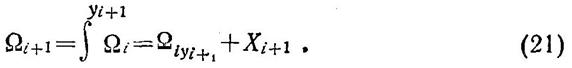
Если оба игрока произвели осознание одновременно, то имеет место соотношение (22), выводимое из (19) и (21):

Процедуру осознания поясняет рис. 3. Пусть в момент времени і ситуация изображается многоголовым человечком в левой части рисунка. (Мы зачернили те головы, в которых что-то отражено). В момент i+1 X произвел осознание. До
Конец страницы 29
¯ Начало страницы 30 ¯
этого все его головы были пусты. Осознание выступит как отражение Т и всех картин Y на следующий этаж по ветви X:
Т отразится в первой голове по ветви X, содержимое первой головы на ветви К отразится во второй голове на ветви X и т. д. (см. правую часть рис. 3).
Введение формальной процедуры для процессов осознания позволяет фиксировать интеллектуальную динамику конфликта. Например, одна из простых схем развертывания конфликта такова:

Это означает, что в момент to партнеры вообще не производили осознания:
Ω0= T0.
В момент t1 оба одновременно осознали плацдарм Т0:

Плацдарм Т в момент tiперешел в состояние T1 но игроки зафиксировали его предыдущее состояние Т0. В следующий момент осознание произвел только X
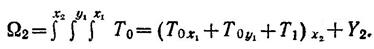
Поскольку Y в момент t 2 осознания не производил, он без изменения «перешел» в момент t2, следовательно,
Y2 = T2+T0y2
и, таким образом,

С помощью изложенного здесь формального метода мы можем фиксировать не только некоторый «объективный» разворот событий, но и динамику развития внутреннего мира игрока в «условных» единицах времени. Воспользовавшись символом П, обозначающим свертку многих сомножителей, мы можем длинные суммы вида (23) представлять короткими интегральными выражениями:

Синхронные рассуждения
Очевидно, что с практической точки зрения наиболее интересны и трудны для анализа случаи взаимной рефлексии игроков. Из сказанного ясно, что преимущество находится на стороне игрока, обладающего более высоким рангом реф-
Конец страницы 30
¯ Начало страницы 31 ¯
лексии. Однако в жизни большей частью в конфликт вступают игроки, обладающие примерно одинаковыми имитационными способностями. Возникающие при этом трудности иллюстрируются следующим примером.
Представим себе следующую ситуацию. Пусть X и Y — противники, вооруженные пистолетами. Если X застрелит Y, то X получит какую-то сумму (пусть это будет 10 пиастров). Если Y застрелит X, то Y получит 10 пиастров. Если оба бездействуют, то оба остаются «при своих». Игроки не несут ни моральной, ни юридической ответственности, если оказываются убийцами, и не руководствуются никакими этическими принципами. Решения принимаются игроками независимо и связаться друг с другом они не могут. Спрашивается, как они должны поступить?
Изобразим игру ввиде матрицы:
| Выстрел Y | Бездействие | |
| Выстрел X | — ∞; — ∞ | 10; — ∞ |
| Бездействие | — ∞; 10 | 0; 0 |
Не правда ли, знакомая дилемма, где один из платежей только эквивалентен смерти?
Игрок X проводит такое рассуждение: «Предположим, я выстрелю, тогда я либо выиграю, либо погибну. Если я не выстрелю, я наверняка не выиграю, но вероятность моей гибели не станет меньше. Ведь У принимает решение независимо от того, что думаю я. Поэтому я должен выстрелить. Но противник проведет именно такое же рассуждение и тоже нажмет на спусковой крючок и я погибну. Да, но ведь он тоже придет к этой же мысли, то есть, что я выстрелю. Может быть, если я не выстрелю, — и он не нажмет на крючок. Нет, не проходит — ведь наши решения не связаны. Конечно, нам обоим выгодно бездействовать. Это очевидно, он это выведет и так поступит. Ага, тогда я выстрелю и выиграю 10 пиастров. Но ведь к такому же решению придет и он...».
Здесь воспроизведено рассуждение игрока, который пытается принять решение и сталкивается с непрерывными противоречиями. Оба варианта решения одинаково неубедительны. Чтобы выявить причину парадокса, представим себе следующую ситуацию: пусть эти двое, вооруженные пистолетами, разделены перегородкой из тонкой зеркальной фольги, которая не является препятствием для пули. Игрок видит свое отражение в зеркале и рассматривает его как модель
Конец страницы 31
¯ Начало страницы 32 ¯
своего противника1. Он медленно поднимает пистолет и видит, что модель противника также поднимает пистолет. Игрок понимает, что если он нажмет на крючок, то и модель нажмет на крючок. Поскольку эта модель—единственное средство прогнозировать поведение противника, то свой выстрел порождает выстрел модели. Игрок медленно опускает пистолет, противник делает то же самое. «Я сейчас его обману», — думает игрок и тут же видит хитроватое выражение лица модели и предупредительное движение пистолета.
Рассуждение игрока, приведенное выше, рождено именно такой ситуацией с зеркалом. Здесь игрок пользуется самим собой как моделью своего противника. Любая мысль, которая приходит ему в голову, автоматически приходит в голову его сопернику. Игроки стоят друг перед другом, синхронно реагируют и синхронно читают мысли друг друга. Игрока X в этой драматической ситуации можно изобразить символической суммой:

Тот факт, что игрок стоит перед зеркалом, фиксируется симметрией каждого слагаемого, заключенного в скобки, относительно индексов х и у. Каждое слагаемое в (24) мы можем интерпретировать как своеобразные «кадры» мысли, «пробегающие» в сознании игроков, как сменяющие друг друга кадры кинофильма. Очевидно, что игрок, на «экране» которого пробегают подобные кадры, может вывести, что сам факт выстрела является приговором самому себе, и примет решение, исходя из этого вывода. В этой особенности синхронных рассуждений и кроется причина парадоксов типа «дилеммы заключенного». Другими словами, логическая природа этой дилеммы может быть объяснена самим механизмом принятия решения игроками, механизмом, осуществляющимся по схеме (24).
Используя ранее введенную символику, мы можем изобразить динамический процесс во внутреннем мире игрока, находящегося в состоянии «дилеммы заключенного», следующим образом:

|
|
|


