 |
Решение (в условии под числом подразумевается натуральное число)
|
|
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
 |
Московский государственный университет
Приборостроения и информатики
Кафедра высшей математики
Выборнов А.Н.
ОБРАЗЕЦ ТЕСТА
ПО ТЕОРИИ ВЕРОЯТНОСТИ
С РЕШЕНИЕМ
Москва 2015
Вопрос №1:
В урне 9 шаров, из которых 5 белых и 4 черных. Из урны вынимают 4 шара. Найти вероятность того, что среди них будет 2 белых и 2 черных.
Решение
Используем общую формулу для задачи:
В урне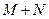 
шаров, из которых 
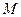и 
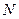белых. Из урны вынимают 
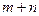шаров. Тогда вероятность того, что среди них будет 
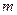белых и 
черных, определяется формулой:
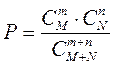
В рассматриваемом вопросе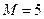 
, 
, 
, 
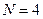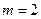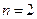. Поэтому
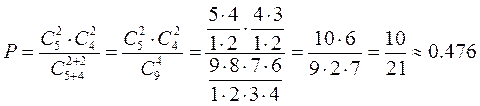
Замечание: Число сочетаний вычисляется по формуле: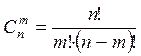 
, где знаком «n!» обозначается факториал числа, равный произведению всех натуральных чисел от 1 до n. Например, 4!=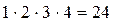 
Принято, что 0!=1!=1.
Замечание 2: число сочетаний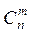 
- всегда равно натуральному числу, не может быть дробным или отрицательным.
Замечание 3: вероятность любого события всегда находится в пределах от 0 до 1, что справедливо для любого вопроса из теста, где требуется найти вероятность. Если в ответе получается отрицательное число, или число большее единицы, следует проверить решение на арифметические ошибки!
Вопрос №2:
Плотность распределения случайной величины X задана формулой
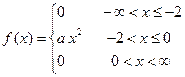
Вычислить математическое ожидание этой случайной величины.
Решение
Сначала необходимо найти константу 
из условия 
.
Итак:
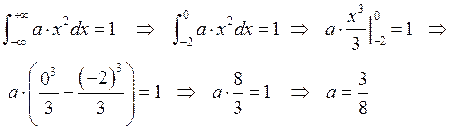
Интеграл вычислялся в пределах от (-2) до 0, так как только на этом промежутке функция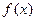 
отлична от нуля.
|
|
|
Теперь мы имеем полное выражение для плотности вероятности случай ной величины Х:
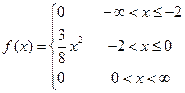
Математическое ожидание непрерывной случайной величины определяется формулой: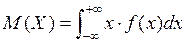 
. Вычисляем:
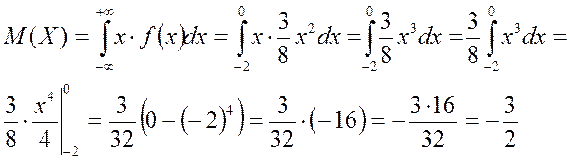
Замечание: математическое ожидание случайной величины является по определению ее средним вероятностным значением. Таким образом, для оценки правильности ответа обратим внимание, что вся случайная величина по условию отлична от ноля только на промежутке от (–2) до 0, следовательно ее среднее значение обязательно должно попасть в этот промежуток.
Вопрос №3:
Плотность распределения случайной величины X задана формулой
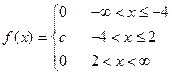
Вычислить вероятность попадания случайной величины Xв интервал (-1; 9).
Решение
Как и в предыдущей задаче, сначала необходимо найти константу 
из условия . Так как плотность вероятности постоянна на отрезке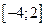 
, рассматриваемая случайная величина распределена по равномерному закону на отрезке 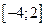, и константа будет равна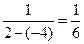 
.
На рисунке изображен жирными линиями график плотности вероятности величины Х. Вероятность попадания этой величины на интервал (-1; 9) равна площади, заключенной между графиком 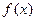и осью абсцисс на этом интервале. На картинке – это площадь заштрихованного прямоугольника. Ширина этого прямоугольника равна 2-(-1)=3, а высота, как мы установили вначале, равна 
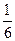. Поэтому его площадь равна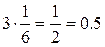 
Вопрос №4:
Случайная величина Х задана дифференциальной функцией распределения
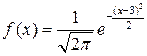. Найти вероятность того, что случайная величина, распределенная таким образом, окажется в интервале (-¥;4).
Решение
Рассматриваемая величина распределена по нормальному закону, для которого плотность вероятности (дифференциальная функция распределения) имеет вид: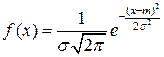 
. Сравнив это выражение с выражением из условия задачи, определяем, что 
, 
.
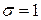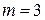Вероятность попадания нормально распределенной величины на интервал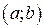 
определяется формулой:
|
|
|
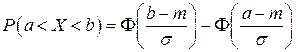
В нашем случае:
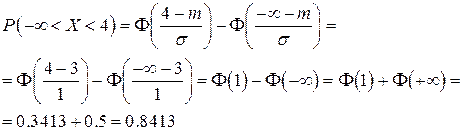
Мы использовали, что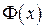 
- нечетная функция, и то, что мы полагаем (приближенно) 
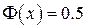при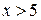 
. Значение 
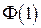найдено нами из таблицы.
Без таблицы вы не сможете правильно выполнить это зачетное задание! Таблица является приложением в любом учебнике по теории вероятностей, как правило, приложение № 2. Таблицей можно официально пользоваться как справочным материалом на зачете или экзамене.
Вопрос №5:
В квадрат с вершинами (0,0), (0,1), (1,1), (1,0) наудачу брошена точка (x,y). Найдите вероятность того, что координаты этой точки удовлетворяют неравенству y >1- 2 x.
Решение
Нарисуем картинку:
На рисунке заштриховано множество точек, координаты которых удовлетворяют неравенству y >1- 2 x.
Искомая вероятность равна отношению площади заштрихованной области к площади всего квадрата. Площадь квадрата очевидно равна 1, а площадь заштрихованной области равна площади квадрата за вычетом площади незаштрихованного треугольника, то есть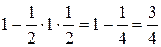 
.
Итак, искомая вероятность равна 
Замечание: чтобы правильно заштриховать область, удовлетворяющую неравенству, сначала нужно знак > или < мысленно заменить на знак равенства и нарисовать соответствующую прямую (самый простой способ – по точкам). Затем для знака < взять область ПОД нарисованной прямой, а для знака > НАД прямой.
Вопрос №6:
Вычислить дисперсию дискретной случайной величины Х, заданной законом распределения:
| X | -1 | -2 | |
| P | 0,1 | 0,3 | 0,6 |
Решение
Сначала вычислим математическое ожидание случайной величины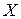 
:
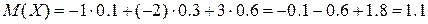
Затем вычислим математическое ожидание случайной величины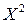 
:
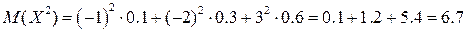
Теперь используем формулу для вычисления дисперсии:
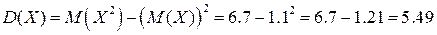
Замечание: Математическое ожидание, являющееся по определению средним значением случайной величины, должно в данном примере попасть в промежуток от -1 до 3, т.к. -1 – минимальное, а 3 – максимальное значение случайной величины, а среднее не может быть меньше минимального или больше максимального значения.
Дисперсия не может получиться отрицательной величиной!
Вопрос №7:
Из букв слова КАРМАН, составленного с помощью разрезной азбуки, наудачу последовательно извлекаются 4 буквы и складываются в ряд. Найти вероятность того, что получится слово КРАН.
|
|
|
Решение
Используем классическое определение вероятности.
Общее число элементарных исходов равно числу размещений из 6 элементов по 4 позициям: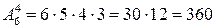 
.
Число благоприятствующих исходов равно 2, так как буква А может быть выбрана двумя способами из слова КАРМАН.
Искомая вероятность равна отношению числа благоприятствующих исходов к общему числу исходов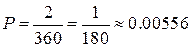 
Замечание (способ № 2). Очевидно, что слово КРАН получится только в том случае, если сначала будет извлечена буква «К», затем буквы «Р», «А» и на последнем месте «Н», причем важен порядок. Вероятность извлечь букву «К» равна 1/6 по классическому определению. Вероятность ПОСЛЕ ЭТОГО извлечь букву «Р» равна 1/5, так как букв останется 5. Вероятность на третий раз получить букву «А» равна 2/4, так как всего две буквы «А» в слове КАРМАН, а останется выбор из 4 букв. Аналогично для последней буквы вероятность 1/3. Перемножая все полученные вероятности, получаем ответ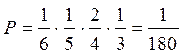 
.
Вопрос №8:
Наудачу выбрано число, не превосходящее 19. Какова вероятность того, что это число делится на 4?
Решение (в условии под числом подразумевается натуральное число)
Используем классическое определение вероятности.
Общее число элементарных исходов равно 19.
Имеется ровно 4 натуральных числа меньших 19 и делящихся на 4, это числа: 4, 8, 12, 16. Значит благоприятных исходов 4.
Поэтому искомая вероятность равна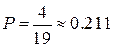 
Вопрос №9:
Случайная величина Х задана дифференциальной функцией распределения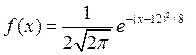 
. Найти М(3Х-9)+D(3Х-9).
Решение
Рассматриваемая величина распределена по нормальному закону, для которого плотность вероятности (дифференциальная функция распределения) имеет вид: 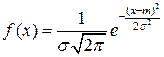. Сравнив это выражение с выражением из условия задачи, определяем, что 
, 
.
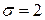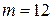Для нормально распределенной величины Х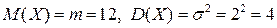 
.
Далее используем свойства математического ожидания и дисперсии:
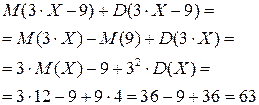
Замечание: при решении задачи использованы свойства (в общем виде):
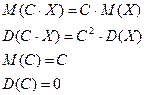
где С – число. Последние два свойства легко запомнить: математическое ожидание константы равно самой этой константе как ее среднее значение. Дисперсия константы равна нолю, т.к. дисперсия характеризует разброс значений относительно среднего, а разброс относительно постоянного числа отсутствует.
|
|
|
Вопрос №10:
Два баскетболиста делают по одному броску в корзину. Вероятность попадания для одного из них равна 0.8, а для другого 0.7.
а) Найти вероятность того, что ровно один из них промахнется.
б) Найти вероятность того, что хотя бы один из них промахнется.
в) Найти вероятность того, что хотя бы один из них попадет.
Решение
Обозначим буквой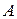 
(событие) попадание первого баскетболиста, буквой 
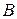(событие) попадание второго баскетболиста.
а) Нам нужно найти вероятность события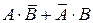 
.
б) Нам нужно найти вероятность хотя бы одного промаха. Здесь удобнее найти сначала вероятность противоположного события – «оба попали»:
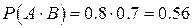
Тогда вероятность хотя бы одного промаха: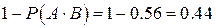 
в) Нам нужно найти вероятность хотя бы одного попадания. Здесь удобнее найти сначала вероятность противоположного события – «оба промахнулись»:
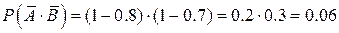
Тогда вероятность хотя бы одного попадания: 
Вопрос №11:
Опыт состоит в последовательном бросании двух монет. Рассматриваются события:
А - выпадение хотя бы одной цифры;
В - выпадение герба на второй монете.
Определить условную вероятность Р(В/А) - вероятность события В при условии, что событие А произошло.
Решение
Выпишем сначала все исходы (Г- герб Ц – цифра):
ГГ
ГЦ
ЦГ
ЦЦ
Событию А благоприятствуют 3 исхода: ГЦ, ЦГ, ЦЦ.
Событию АВ (хотя бы одна цифра и герб на второй монете) благоприятствует 1 исход: ЦГ.
Условная вероятность равна: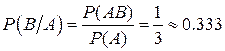 
Вопрос №12:
При передаче сообщения вероятность искажения для каждого знака равна 0,1. Найти вероятность того, что сообщение из 5 знаков содержит ровно 3 искажения.
Решение
Для решения этой задачи нужно использовать формулу Бернулли:
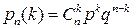
В этой задаче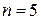 
, 
, 
, 
.
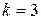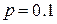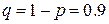Итак:
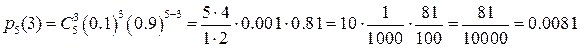
При вычислении мы использовали свойство: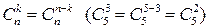 
.
Замечание: формула Бернулли применяется только тогда, когда проводится несколько испытаний, и вероятность события в каждом испытании ОДИНАКОВАЯ.
Вопрос №13:
Из 5 стрелков 2 попадают в цель с вероятностью 0.7, а 3 - с вероятностью 0.4. Найти вероятность того, что наудачу выбранный стрелок попадет в цель.
Решение
Для решения задачи применим формулу полной вероятности:
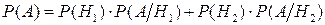
В рассматриваемой задаче обозначим:
событие 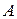- «наудачу выбранный стрелок попадет в цель»,
событие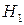 
- «наудачу выбранный стрелок - это один из тех стрелков, которые попадают в цель с вероятностью 0.7»,
|
|
|
событие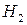 
- «наудачу выбранный стрелок - это один из тех стрелков, которые попадают в цель с вероятностью 0.4».
Теперь заметим, что
,
.
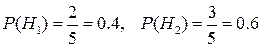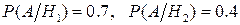Получаем:
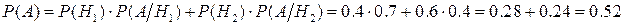
Замечание: сумма вероятностей всех гипотез должна быть равна единице. В нашем случае,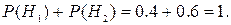 
|
|
|
