 |
Задания для самостоятельного решения
|
|
|
|
ВЕКТОРНАЯ АЛГЕБРА (СЕМИНАРЫ)
- ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
РАЗЛОЖЕНИЕ ВЕКТОРОВ
Вектор – направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом  (или одной буквой:
(или одной буквой:  ,
,  , …, или: a, b, …). Длина отрезка АВ называется длиной (модулем) вектора
, …, или: a, b, …). Длина отрезка АВ называется длиной (модулем) вектора  и обозначается |
и обозначается |  |, |
|, |  |, | a |.
|, | a |.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  (0).
(0).
Вектор, длина которого равна единице, называется единичным вектором и обозначается
через 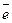 (е).
(е).
Единичный вектор, направление которого совпадает с направлением вектора  ,
,
называется ортом вектора  и обозначается
и обозначается  .
.
Два вектора, имеющие одинаковую длину и противоположные направления, называются
противоположными. Вектор, противоположный вектору  , обозначается -
, обозначается -  .
.
Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых. Записывают:  ||
||  .
.
Три (и более) вектора называются компланарными, если они лежат в одной плоскости
или в параллельных плоскостях.
Два коллинеарных вектора  и
и  называются равными (
называются равными ( =
=  ), если они одинаково
), если они одинаково
направлены и имеют равные длины.
Совместим параллельным переносом начала неколлинеарных векторов  и
и  . Начало и концы векторов образуют вершины треугольника. Углом между векторами
. Начало и концы векторов образуют вершины треугольника. Углом между векторами  и
и 
называется угол при вершине этого треугольника, соответствующий началу векторов. Если
векторы сонаправлены, то угол между ними равен нулю, если противоположно направлены –
угол между ними равен 180º.
Суммой двух векторов  и
и  называется вектор
называется вектор  , соединяющий начало вектора
, соединяющий начало вектора  с
с
концом вектора  , отложенного от конца вектора
, отложенного от конца вектора  .
.
|
|
|
Обозначение:  =
=  +
+  .
.
Геометрически сумма векторов получается с помощью правил «треугольника» или
«параллелограмма»:
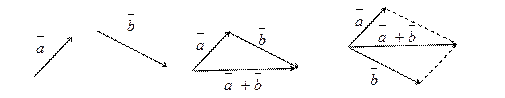
Под разностью векторов  и
и  понимается вектор
понимается вектор  такой, что
такой, что  +
+  =
=  .
.
Обозначение:  =
=  –
–  .
.
Справедливо равенство:  –
–  =
=  + (–
+ (–  ).
).
Произведением вектора  ≠
≠  на число λ ≠ 0 называется вектор, имеющий длину
на число λ ≠ 0 называется вектор, имеющий длину
| λ | ∙ |  | и направление, совпадающее с направлением вектора
| и направление, совпадающее с направлением вектора  , если λ > 0, противоположное ему, если λ < 0. Обозначение: λ ∙
, если λ > 0, противоположное ему, если λ < 0. Обозначение: λ ∙  .
.
Каждый вектор равен произведению его модуля на его орт:  = |
= |  | ∙
| ∙  .
.
Признак коллинеарности векторов: два ненулевых вектора 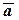 и
и  коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число:
коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число:
 = λ
= λ 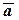 .
.
Признак компланарности векторов: три ненулевых вектора 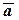 ,
,  ,
,  компланарны тогда и только тогда, когда один из них является линейной комбинацией других, т.е.
компланарны тогда и только тогда, когда один из них является линейной комбинацией других, т.е.
 = λ 1
= λ 1 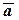 + λ 2
+ λ 2  (λ 1 и λ 2 – одновременно не равные нулю числа).
(λ 1 и λ 2 – одновременно не равные нулю числа).













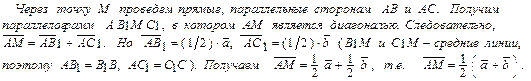



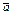









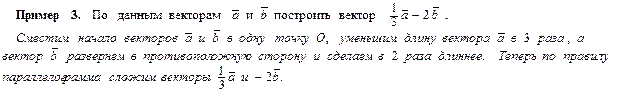

 | |||
 | |||
Основные свойства проекции:
1.  =
= 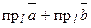 ; 2.
; 2.  = λ ∙
= λ ∙  .
.
Если  ,
,  ,
,  – орты координатных осей прямоугольной системы координат Oxyz, то любой вектор
– орты координатных осей прямоугольной системы координат Oxyz, то любой вектор  единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами ах, ау, аz:
единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами ах, ау, аz:
 = ах ∙
= ах ∙  + аy ∙
+ аy ∙  + аz ∙
+ аz ∙  . Коэффициенты ах, ау и аz линейной комбинации называются координатами вектора
. Коэффициенты ах, ау и аz линейной комбинации называются координатами вектора  в базисе
в базисе  ,
,  ,
,  .
.
Обозначение:  = { ах, ау, аz } или
= { ах, ау, аz } или  = ах ∙
= ах ∙  + аy ∙
+ аy ∙  + аz ∙
+ аz ∙  .
.
Координаты вектора  в базисе
в базисе  ,
,  ,
,  ,
,  = { ах, ау, аz }, совпадают с координатами т. М – конца вектора
= { ах, ау, аz }, совпадают с координатами т. М – конца вектора  =
=  в прямоугольной системе координат Oxyz: М (ах, ау, аz).
в прямоугольной системе координат Oxyz: М (ах, ау, аz).
Длина вектора  определяется по формуле |
определяется по формуле |  | =
| =  .
.
Вектор  образует с координатными осями Ox, Oy и Oz углы α, β и γ соответстенно.
образует с координатными осями Ox, Oy и Oz углы α, β и γ соответстенно.
Направление вектора  определяется с помощью направляющих косинусов: cos α, cos β, cos γ, вычисляемых по формулам: cos α =
определяется с помощью направляющих косинусов: cos α, cos β, cos γ, вычисляемых по формулам: cos α =  , cos β =
, cos β =  , cos γ =
, cos γ = 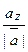 .
.
|
|
|
Направляющие косинусы связаны соотношением cos2 α + cos2 β + cos2 γ = 1.
Координаты орта вектора  – это его направляющие косинусы:
– это его направляющие косинусы:
 =
=  .
.
Пусть векторы  и
и  заданы своими координатами:
заданы своими координатами:  = { ах, ау, аz } и
= { ах, ау, аz } и  = { bх, bу, bz }.
= { bх, bу, bz }.
Векторы  и
и  равны тогда и только тогда, когда равны их соответствующие координаты, т.е.
равны тогда и только тогда, когда равны их соответствующие координаты, т.е.  =
=  ó
ó  .
.
Векторы  и
и  коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
 ||
||  ó
ó 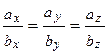 .
.
При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении вектора на число – умножаются на это число:


 = { ах
= { ах  bх, аy
bх, аy  by, аz
by, аz  bz }, λ
bz }, λ  = { λ ах, λ ау, λ аz }.
= { λ ах, λ ау, λ аz }.
Вектор  =
=  , соединяющий начало координат с произвольной точкой М (x, y, z)пространства называется радиус-вектором точки М. Координаты точки – это координаты ее радиус-вектора
, соединяющий начало координат с произвольной точкой М (x, y, z)пространства называется радиус-вектором точки М. Координаты точки – это координаты ее радиус-вектора  = { x, y, z } или
= { x, y, z } или  = x ∙
= x ∙  + y ∙
+ y ∙  + z ∙
+ z ∙  .
.
Если вектор  =
=  задан точками А (x 1, y 1, z 1) и В (x 2, y 2, z 2), то его координаты ах, ау, аz вычисляются по формулам
задан точками А (x 1, y 1, z 1) и В (x 2, y 2, z 2), то его координаты ах, ау, аz вычисляются по формулам
ах = x 2 – x 1, ay = y 2 – y 1, aх = z 2 – z 1:  =
=  = { x 2 – x 1, y 2 – y 1, z 2 – z 1}.
= { x 2 – x 1, y 2 – y 1, z 2 – z 1}.
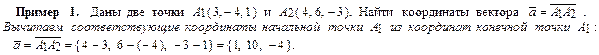
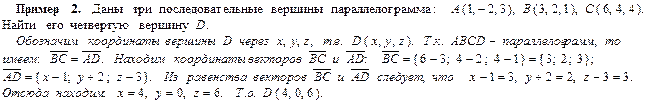


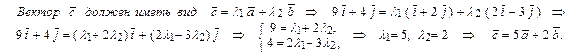
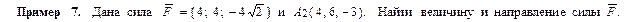
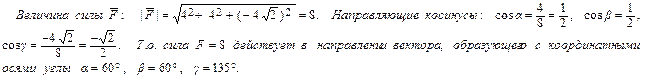

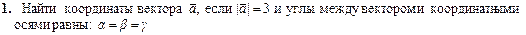
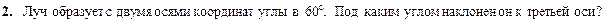

- СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ


Таким образом, ( ,
,  ) = |
) = |  | ∙ |
| ∙ |  | ∙ cos φ (1)
| ∙ cos φ (1)
Формулу (1) можно записать в виде: ( ,
,  ) = |
) = |  | ∙ пр
| ∙ пр 
 или (
или ( ,
,  ) = |
) = |  | ∙ пр
| ∙ пр 
 . (2)
. (2)
Из формул (2) имеем: пр 
 =
=  , пр
, пр 
 =
=  .
.
Свойства скалярного произведения:
1. ( ,
,  ) = (
) = ( ,
,  ). 2. (
). 2. ( , (
, ( +
+  )) = (
)) = ( ,
,  ) + (
) + ( ,
,  ). 3. ((λ
). 3. ((λ  ),
),  ) = λ (
) = λ ( ,
,  ).
).
4.  = |
= |  |2 – скалярный квадрат вектора
|2 – скалярный квадрат вектора  равен квадрату его модуля.
равен квадрату его модуля.
- Скалярное произведение векторов равно нулю тогда и только тогда, когда cos φ = 0 (φ = π /2) (перемножаемые векторы перпендикулярны):
( ,
,  ) = 0 ó
) = 0 ó  ┴
┴ 
(или  =
=  , или
, или  =
=  ). В частности: (
). В частности: ( ,
,  ) = (
) = ( ,
,  ) = (
) = ( ,
,  ) = 0.
) = 0.
Если векторы  и
и  заданы своими координатами
заданы своими координатами  = { ах, ау, аz },
= { ах, ау, аz },  = { bх, bу, bz }, то (
= { bх, bу, bz }, то ( ,
,  ) = ах bх + ау bу + аz bz.
) = ах bх + ау bу + аz bz.
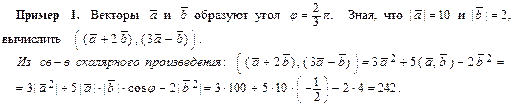
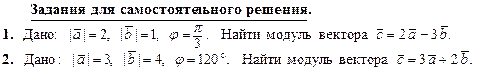
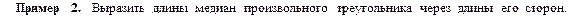















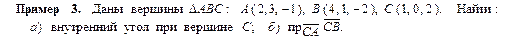
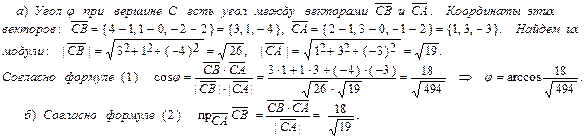
Задания для самостоятельного решения











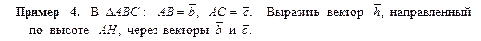

|
|
|


