 |
O.B. Katchalov, M.I. Chanova, N.P. Yampurin
|
|
|
|
О.Б. Качалов, М.И. Чанова, Н.П. Ямпурин
РАЗРАБОТКА ПРОГНОЗНОЙ МОДЕЛИ КАЧЕСТВА ПРИБОРОВ НА ОСНОВЕ ЭКСТРЕМУМА ПОГРЕШНОСТИ
(Арзамасский политехнический институт (филиал) НГТУ им. Р.Е.Алексеева, г.Арзамас)
Аннотация: В работе предлагается прогнозная модель надежности качества полупроводниковых приборов. На основе зависимости средней абсолютной погрешности проверочных точек от средней абсолютной погрешности точек обучающей выборки выбирается интервал погрешности обучающих точек, при котором имеет место существенное снижение погрешности проверочных точек. При этом изменения средней абсолютной погрешности точек обучающей выборки осуществляется несколькими вариантами. Отмеченный эффект позволяет уменьшить интервал обучения прогнозной модели и существенно увеличить интервал прогноза. Вышеизложенное подтверждается расчетными и экспериментальными данными по прогнозу качества стабилитронов 2С182Ж.
Ключевые слова: прогнозная модель, экстремум погрешности проверочных точек, качество РЭС, снижение интервала обучения.
В современных условиях усложнение радиоэлектронных средств приводит к ряду проблем при оценке надежности и качества изделий из-за наличия ряда трудно выявляемых скрытых дефектов. В связи с этим возникает задача разработки прогнозной модели и анализа ее эффективности на основе экстремума погрешности [1].
В работе [1] показано, что любая аппроксимирующая зависимость (регрессионная, нейросетевая, модели самоорганизации и т.д.) имеет интервал погрешности обучающих точек, при котором погрешности проверочных точек сравнительно малы. При этом имеет место существенное снижение погрешности проверочных точек. Отмеченный эффект использовался для снижения погрешности измерительных систем, датчиков, повышения точности расчетов при использовании аппроксимирующих зависимостей [2-5] Очевидно, влияние этого эффекта будет иметь место и при разработке прогнозных моделей.
|
|
|
В качестве примера рассмотрим данные обучающего эксперимента, заимствованные из работы Мишанова Р.О., Пиганова М.Н. [6]. Была использована выборка, состоящая из 50 стабилитронов2С182Ж. В качестве прогнозного параметра измерялись значения напряжения стабилизации ∆Uст. Величина ∆Uст оценивалась за 25,100,250,500 и 1000 часов испытаний. Было установлено граничное значение ∆Uст.гр=20 мВ при значении t=1000 ч. При ∆Uст< 20 мВ - изделие принималось как годное. При ∆Uст > 20 мВ - негодное. Ставится задача по значениям напряжения стабилизации при t=25 часов, t=100 часов прогнозировать значения этого параметра при t=1000 ч. Обучающая выборка, по которой синтезируется модель, представлена в таблице 1. Данные по проверочным точкам представлены в таблице 2. Расчеты проводились с помощью нейросетей. Рассматривалась нейросетевая модель со стандартной функцией программы MATLAB, имеющей следующий вид:
net = newrb(P,T,GOAL,SPREAD),
где P - матрица входных данных;
T - вектор выходных данных;
GOAL - среднеквадратическая ошибка (в нашей модели принята равной 0,3);
SPREAD - параметр влияния радиально-базисной функции (в нашей модели
принят равным 2,3).
Таблица 1. Обучающая выборка
| № | 1000 ч | 25 ч | 100 ч | № | 1000 ч | 25 ч | 100 ч | |
|
|
|
Таблица 2. Проверочная выборка
| № | 1000 ч | 25 ч | 100 ч | № | 1000 ч | 25 ч | 100 ч | |
В процессе калибровочных работ была снята зависимость средней абсолютной погрешности проверочных точек от средней абсолютной погрешности точек обучающей выборки (рис.1).При этом для низких значений погрешности проверочных точек имеет место совпадение расчетных и экспериментальных данных (в смысле годности, негодности), что показано в таблице 3. При больших погрешностях проверочных точек такое совпадение не наблюдалось.
Изменение средней абсолютной погрешности точек осуществлялось за счет изменения состава обучающей выборки. При этом могут быть случаи увеличения и уменьшения количества точек. Рассматривался и такой вариант изменения средней абсолютной погрешности обучающих точек. В первом ряду обучающей матрицы выбиралось несколько наибольших значений напряжения стабилизации. В данных одного эксперимента это значение изменялось и при этом средняя абсолютная погрешность проверочных точек уменьшалась. Далее аналогичная процедура. применялась к другой выбранной величине. Расчеты продолжались до тех пор пока не была достигнута необходимая величина снижения погрешности проверочных точек. Здесь важно подчеркнуть, что, воздействуя на обучающую выборку, мы получаем снижение погрешности проверочных точек.
Предлагаемая модель прогнозирования качества полупроводниковых приборов позволит существенно сократить интервал обучения, может найти широкое применение при анализе качества авиационной аппаратуры при большом интервале прогноза.
|
|
|
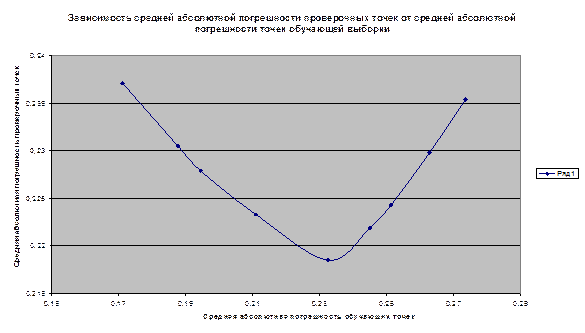
Рисунок 1
Таблица 3. Сравнение экспериментальных и расчетных данных
| Экспериментальное значение | Расчетное значение | Экспериментальное значение | Расчетное значение | |
| 33.0000 | 35.4811 | 12.0000 | 11.2903 | |
| 8.00000 | 11.2903 | 25.0000 | 27.4492 | |
| 13.0000 | 10.3698 | 24.0000 | 20.2864 | |
| 6.0000 | 7.2592 | 5.0000 | 6.7107 | |
| 4.0000 | 5.9296 | 18.0000 | 19.7940 | |
| 16.0000 | 14.7549 | 6.0000 | 7.2592 | |
| 5.0000 | 6.7107 | 24.0000 | 24.6165 | |
| 7.0000 | 7.2592 | 3.0000 | 5.9296 | |
| 10.0000 | 12.7879 | 10.0000 | 10.3698 | |
| 19.0000 | 18.5016 | 9.0000 | 7.2592 | |
| 8.0000 | 6.707 | 28.0000 | 35.0766 | |
| 42.0000 | 40.9569 | 11.0000 | 7.2592 | |
| 28.0000 | 37.6681 |
Библиографический список:
1. О.Б., Качалов Методы снижения погрешности аппроксимирующих зависимостей/ О.Б. Качалов, Н.П. Ямпурин// Международная научно-техническая конференция «АНТЭ-2013», сборник докладов. - 2013. - С.200-203.
2. Патент № 2466356 Российская Федерация МПК G01F1/20. Способ измерения расхода двухфазной трехкомпонентной среды; заявитель и патентообладатель: Нижегородский государственный технический университет им. Р.Е. Алексеева (RU). - № 2011111517/28; заявл. 25.03.2011; опубл. 10.11.2011, Бюл. № 31. - 6с.; авт.: Качалов О.Б., Ямпурин Н.П., Плесовских К.Ю., Баранова А.В., Войнова Ю.А., Улюшкин А.В..
3. Патент № 2527138 Российская Федерация МПК G01N29/02. Способ измерения влажности нефти; заявитель и патентообладатель: Нижегородский государственный технический университет им. Р.Е. Алексеева (RU). - № 2013113823/28; заявл. 27.03.2013; опубл. 27.08.2014, Бюл № 24. -2с.; авт.: Качалов О.Б., Ямпурин Н.П., Баранова А.В., Волков Д.Е., Корноухова Е.А., Шабаева И. А., Плесовских К.Ю.
4. Патент № 2527667 Российская Федерация МПК G01F1/20. Способ измерения расхода двухфазной трехкомпонентной среды; заявитель и патентообладатель: Нижегородский государственный технический университет им. Р.Е. Алексеева (RU). - № 2012136700/28; заявл. 27.08.2012; опубл. 10.09.2014. Бюл № 25. -2с.; авт.: Качалов О.Б., Ямпурин Н.П., Баранова А.В., Улюшкин А.В., Акишин Е.В.
5. А.В. Баранова Многовариантность при поиске экстремума погрешности аппроксимации/ А.В. Баранова, А.В Голова, О.Б. Качалов// Приволжский научный вестник, № 12-3 (40) - 2014. С.5-8.
|
|
|
6. Р.О. Мишанов Разработка прогнозной модели качества полупроводниковых приборов методом экстраполяции/ Р.О. Мишанов, М.Н. Пиганов// Известия Самарского научного центра Российской академии наук, выпуск № 4-3, том 16, Самара-2014.- С.594-598.
O.B. Katchalov, M.I. Chanova, N.P. Yampurin
|
|
|


