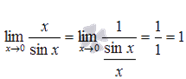|
Основные свойства функций.
|
|
|
|
Алгебраическая форма
3. Запись комплексного числа 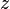 в виде
в виде 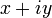 ,
,  , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.
4. Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):
):
5. 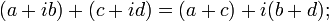
6. 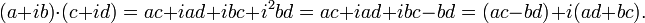
Комплексные числа — расширение множества вещественных чисел, обычно обозначается 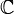 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 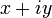 , где
, где 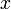 и
и 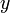 — вещественные числа,
— вещественные числа, 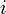 — мнимая единица, то есть одно из чисел, удовлетворяющих уравнению
— мнимая единица, то есть одно из чисел, удовлетворяющих уравнению 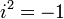 . Общепринятым произношением является компле́ксное число́, что позволяет различить математический смысл слова комплексный и бытовой.
. Общепринятым произношением является компле́ксное число́, что позволяет различить математический смысл слова комплексный и бытовой.
Действия:
Сложение комплексных чисел
Вычитание комплексных чисел
Умножение комплексных чисел
3. Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соеденяющий точку окружности с ее центром.
Хордой называется отрезок соединяющий любые две точки окружности.
Диаметром называется хорда, проходящая через центр окружности.
4. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
5. функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
|
|
|
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодическость функции.
|
|
|
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.
6. Последовательность — это набор элементов некоторого множества:
· для каждого натурального числа можно указать элемент данного множества;
· это число является номером элемента и обозначает позицию данного элемента в последовательности;
· для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
7.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Свойства бесконечно малых
· Сумма конечного числа бесконечно малых — бесконечно малая.
· Произведение бесконечно малых — бесконечно малая.
· Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
· Если  — бесконечно малая последовательность, сохраняющая знак, то
— бесконечно малая последовательность, сохраняющая знак, то 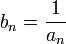 — бесконечно большая последовательность.
— бесконечно большая последовательность.
8.
· Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
|
|
|
· 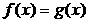 Þ
Þ 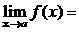
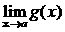 .
.
· Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x).
· 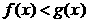 Þ
Þ 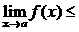
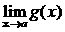 .
.
· Теорема 3. Предел постоянной равен самой постоянной.
·  .
.
· Теорема 4. Функция не может иметь двух различных пределов в
· одной точке.
· Доказательство. Предположим противное. Пусть
· 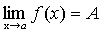 и
и 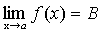 .
.
· еорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при  , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при  , причем предел алгебраической суммы равен алгебраической сумме пределов.
, причем предел алгебраической суммы равен алгебраической сумме пределов.
· 

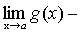
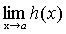 .
.
9\10
· Первый замечательный предел:
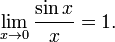
Следствия первого замечательного предела:
·
·
· Второй замечательный предел:
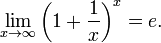
11.

12.
|
|
|