 |
Способ существенной выборки, использующий «вспомогательную плотность распределения».
|
|
|
|
В качестве оценки интеграла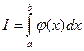 
принимают 
, где n – число испытаний; f(x) – плотность распределения «вспомогательной» случайной величины X, причём 
; 
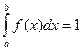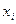- возможные значения X, которые разыгрывают по формуле 
.
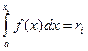Функцию f(x) желательно выбирать так, чтобы отношение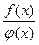 
при различных значениях x изменялось незначительно. В частности, если 
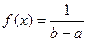, то получим оценку 
.
Задача. Найти оценку 
интеграла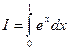 
.
Решение. Так как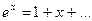 
, то в качестве плотности распределения «вспомогательной» случайной величины X примем функцию 
. Из условия 
найдём 
. Итак,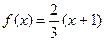 
.
Запишем искомый интеграл так:
.
Таким образом, интеграл I представлен в виде математического ожидания функции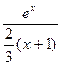 
. В качестве искомой оценки примем выборочную среднюю (для простоты ограничимся десятью испытаниями):
,
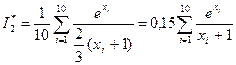где 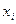- возможные значения X, которые надо разыграть по известной плотности 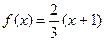. По правилу (для того, чтобы разыграть возможное значение 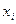непрерывной случайной величины X, зная её плотность вероятности f(x), надо выбрать случайное число 
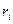и решить относительно 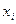уравнение
, или уравнение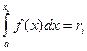 
,
где a – наименьшее конечно возможное значение X), имеем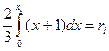 
. Отсюда находим явную формулу для разыгрывания возможных значений X:
.
В таблице 2 приведены результаты 10 испытаний.
Сложив числа последней строки таблицы 2, получим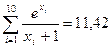 
. Искомая оценка равна 
.
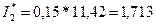Таблица 2.
| Номер i |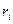
|
| 
| 
| 
|
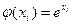
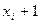
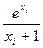
| 0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876 | 0,140 0,980 0,326 0,459 0,600 0,185 0,894 0,550 0,436 0,905 | 1,150 2,664 1,385 1,582 1,822 1,203 2,445 1,733 1,546 2,472 | 1,140 1,980 1,326 1,459 1,600 1,185 1,894 1,550 1,436 1,905 | 1,009 1,345 1,044 1,084 1,139 1,015 1,291 1,118 1,077 1,298 |
Способ, основанный на истолковании интеграла как площади.
Пусть подынтегральная функция неотрицательна и ограничена: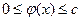 
, а двумерная случайная величина 
распределена равномерно в прямоугольнике D с основанием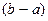 
и высотой 
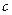. Тогда двумерная плотность вероятности 
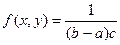для точек, принадлежащих D; 
вне D.
|
|
|
В качестве оценки интеграла 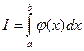принимают 
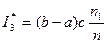, где n – общее число случайных точек 
, принадлежащих D;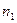 
- число случайных точек, которые расположены под кривой 
.
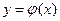Задача. Найти оценку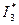 
интеграла 
.
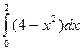Решение. Используем формулу 
.
В интервале (0,2) подынтегральная функция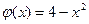 
неотрицательна и ограничена, причём 
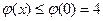; следовательно, можно принять c=4.
Введём в рассмотрение двумерную случайную величину (X,Y), распределённую равномерно в прямоугольнике D с основанием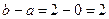 
и высотой с=4, плотность вероятности которой 
.
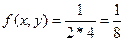Разыгрываем n=10 случайных точек , принадлежащих прямоугольнику D. Учитывая, что составляющая X в интервале (0,2) распределена равномерно с плотностью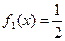 
и составляющая Y в интервале (0,4) распределена равномерно с плотностью 
, разыграем координаты случайной точки , принадлежащей прямоугольнику D, по паре независимых случайных чисел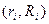 
: 
, 
.Отсюда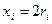 
, 
.
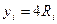| Номер i |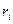
|
| 
| 
| 
|
| 
|
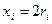
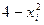
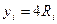
| 0,100 0,253 0,520 0,863 0,354 0,809 0,911 0,542 0,056 0,474 | 0,200 0,506 1,040 1,726 0,708 1,618 1,822 1,084 0,112 0,948 | 0,040 0,256 1,082 2,979 0,501 2,618 3,320 1,175 0,013 0,899 | 3,960 3,744 2,918 1,021 3,499 1,382 0,680 2,825 3,987 3,101 | 0,973 0,376 ,135 0,467 0,876 0,590 0,737 0,048 0,489 0,296 | 3,892 1,504 0,540 1,868 3,504 2,360 2,948 0,192 1,956 1,184 |
Если окажется, что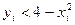 
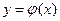, то точка лежит под кривой и в «счётчик 
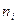» надо добавить единицу.
Результаты десяти испытаний приведены в таблице 3.
Из таблицы 3 находим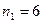 
. Искомая оценка интеграла
§5. Способ «выделения главной части».
В качестве оценки интеграла 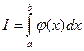принимают
,
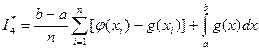где 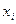- возможные значения случайной величины X, распределённой равномерно в интервале интегрирования 
, которые разыгрывают по формуле 
; функция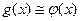 
, причём интеграл 
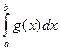можно вычислить обычными методами.
Задача. Найти оценку 
интеграла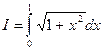 
.
Решение. Так как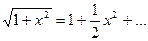 
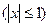, то примем 
. Тогда, полагая число испытаний n=10, имеем оценку
|
|
|
.
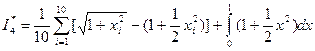Выполнив элементарные преобразования, получим
.
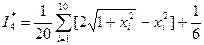Учитывая, что a=0, b=1, возможные значения 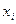разыграем по формуле 
. Результаты вычислений приведены в таблице 4.
| Номер i |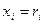 
|
| 
| 
| 
|
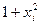
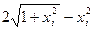
| 0,100 0,973 0,253 0,376 0,520 0,135 0,863 0,467 0,354 0,876 | 0,010 0,947 0,064 0,141 0,270 0,018 0,745 0,218 0,125 0,767 | 1,010 1,947 1,064 1,141 1,270 1,018 1,745 1,218 1,125 1,767 | 1,005 1,395 1,032 1,068 1,127 1,009 1,321 1,104 1,061 1,329 | 2,000 1,843 2,000 1,995 1,984 2,000 1,897 1,990 1,997 1,891 |
Сложив числа последнего столбца таблицы 4, найдём сумму 19,597, подставив которую в соотношение 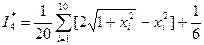, получим искомую оценку интеграла
.
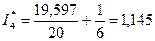Заметим, что точное значение I=1,147.
|
|
|
