Как применить законы Кирхгофа для цепей с синусоидальными токами и напряжениями?

Что такое резонанс напряжений?

Резонансом напряжений называют резонанс в схеме последовательного соединения R, L, С (рис. 3.16 а).

При резонансе ток в цепи должен совпадать по фазе с ЭДС Е. Это возможно, если входное сопротивление схемы Z = R + j (ωL-1/ωC) будет чисто активным. Условие наступления резонанса в схеме(рис. 3.16 а).

(3.61)

где ω₀ - резонансная частота.

Рис.3.16

При этом 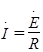. Модуль напряжения на индуктивном элементе при резонансе равен напряжению на емкостном элементе:

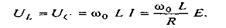
Отношение

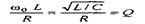(3.62)

Пусть в этой схеме параметры R, L, С и ЭДС E постоянны, а меняется частота ω. Рассмотрим характер изменений модулей тока I и напряжений U_L и U_c в функции от ω.

Ток в цепи

При изменении ω меняется реактивное сопротивление цепи следующим образом:

при ω → 0 сопротивление X → ∞ и ток I → 0;

при сопротивление X = 0, ток I= E/R;

при ω → ∞ сопротивление X → ∞, ток I → 0.

Напряжение

при ω → 0 напряжение U_L= 0;

при ω → ∞ напряжение U_L → E (рис. 3.16, в);

при ω → 0,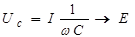

при ω → ∞ напряжение U_с → 0.

Из рис. 3.16, в видно, что максимумы напряжений U_L и U_c имеют место при частотах, не равных резонансной частоте :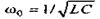

максимум U_l имеет место при частоте ω _L > ω ₀, а максимум U_c - при частоте ω _с < ω_0.:

На рис. 3.16, г изображены две кривые, характеризующие зависимость I = f(ω) ля цепи с неизменными L, С и Е при двух различных значениях R. Для кривой 2 сопротивление R меньше (а добротность Q больше), чем для кривой 1.

Обычно кривые изображают в относительных единицах: ток в долях от тока при резонансе, частота - в долях от резонансной частоты. Графики тока в относительных единицах изображены на рис. 3.16 д. Они построены по формуле

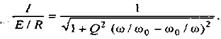
Чем меньше активное сопротивление резонансного контура при не­изменных остальных параметрах схемы, т. е. чем больше добротность контура Q, тем более острой (пикообразной) становится форма кривой I = f(ω).

Полосой пропускания резонансного контура называют полосу частот

ω₂ – ω₁ = ω₀ / Q, на границах которой отношение 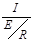составляет 0,707(рис. 3.16 д).

Граничные частоты 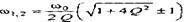. Аргумент входного сопротив-ления схемы (рис. 3.16, а) .

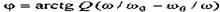Если в данной схеме изменять не частоту, а индуктивность L, то за-висимости I, U_L, в функции от Х_L =ωL (со = const) будут иметь вид кривых рис. 3.16 е.

Каково условие возникновения резонанса напряжений?

При резонансе ток в цепи должен совпадать по фазе с ЭДС Е. Это возможно, если входное сопротивление схемы Z = R + j (ωL-1/ωC) будет чисто активным. Условие наступления резонанса в схеме(рис. 3.16 а).

Как применить законы Кирхгофа для цепей с синусоидальными токами и напряжениями?

По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:

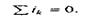(3.43)

Подставим вместо i_k в (3.43) и вынеся e^jωt за скобку, получим e^jωt 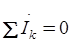Так e^jωt не равно нулю при любом t, то

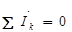(3.44)

Уравнение (3.44) представляет собой первый закон Кирхгофа в сим-волической форме записи.

Для замкнутого контура сколь угодно сложной электрической цепи синусоидального тока можно составить уравнение по второму закону Кирхгофа для мгновенных значений токов, напряжений и ЭДС.

Пусть замкнутый контур содержит п ветвей и каждая k -ветвь в общем случае включает источник ЭДС е_к, резистор R_k, индуктивный L_k и емкостный С_к элементы, по которым протекает ток i_k. Тогда, по второму закону Кирхгофа,

(3.45)

Но каждое слагаемое левой части уравнения можно заменить на 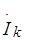Z_k, а каждое слагаемое правой части - на Е_к. Поэтому уравнение (3.45) переходит в

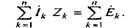(3.46)

Уравнение (3.46) представляет собой второй закон Кирхгофа в сим-волической (комплексной) форме записи.

Первый и второй законы Кирхгофа и все расчетные формулы, приведенные ранее, справедливы для цепей синусоидального тока в том случае, когда отдельные ветви электрической цепи синусоидального тока не связаны между собой магнитно.

Если же отдельные ветви электрической цепи синусоидального тока связаны друг с другом магнитно (это имеет место при наличии взаимо­индукции), то падение напряжения на каком-либо участке цепи зависит не только от тока данной ветви, но и от токов тех ветвей, с которыми данная ветвь связана магнитно. Расчет электрических цепей синусоидального тока при наличии в них магнитно-связанных ветвей приобретает ряд особенностей. Особенности расчета магнитно-связанных цепей рассмотрены позже.

10. Дать определение коэффициенту мощности (cos φ). Каков его энергетический смысл?

Коэффициент мощности — величина, равная отношению активной мощности P, потребляемой нагрузкой, к ее полной мощности S.

Полная мощность — это произведение действующих значений напряжения и тока:

S=U×I, измеряется в вольт-амперах (ВА).

Активная мощность измеряется в ваттах (Вт) и вычисляется по формуле:

P=U×I×λ, где λ — это коэффициент мощности.

Коэффициент мощности это соотношение полезной активной мощности к полной мощности, то есть cosφ=P/S.

В случае синусоидального напряжения, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой, и равен коэффициенту искажений тока.

В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением).

11. Почему стремятся повышать cosφ?

Коэффициент мощности – это отношение полезной (активной) мощности к полной (кажущейся) мощности, потребляемой электрооборудованием объекта или электроустановкой. Он является мерой эффективности преобразования электрической энергии в полезную работу. Идеальное значение коэффициента мощности равно единице. Любая величина, меньшая, чем единица, означает, что для получения желаемого результата необходима дополнительная мощность.Протекание токов приводит к потерям в генерирующих мощностях и распределительной системе. Нагрузка с коэффициентом мощности 1,0 наиболее эффективно загружает источник, а нагрузка с коэффициентом мощности, к примеру, 0,8 является причиной больших потерь в системе и более высоких расходов на электроэнергию. Сравнительно небольшое улучшение коэффициента мощности может привести к значительному снижению потерь, так как они пропорциональны квадрату тока.Если коэффициент мощности меньше единицы, это указывает на присутствие так называемой реактивной мощности. Она требуется для получения магнитного поля, необходимого для работы двигателей и других индуктивных нагрузок. Реактивная мощность, которую также можно назвать бесполезной мощностью или мощностью намагничивания, создаёт дополнительную нагрузку на систему электропитания и увеличивает затраты потребителя за электроэнергию.

• экологические: снижение потребления электроэнергии за счёт повышения эффективности её использования. Снижение потребления приводит к уменьшению выбросов парниковых газов и замедлению истощения ресурсов ископаемого топлива для электростанций;
• уменьшение расходов на электроэнергию;
• возможность получения большей мощности от имеющегося источника;
• снижение тепловых потерь в трансформаторах и оборудовании распределения;
• уменьшение падения напряжения в длинных кабелях;
• увеличение срока службы оборудования в связи со снижением электрической нагрузки на кабели и другие электрические компоненты.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: