 |
Геометрическое представление
|
|
|
|
Под моделью понимается вид функции отклика
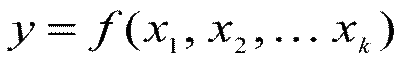 .
.
Выбрать модель – значит выбрать вид этой функции, записать её уравнение.
Тогда останется спланировать и провести эксперимент для оценки численных значений констант (коэффициентов) этого уравнения. Но как выбрать модель?
Для решения этого вопроса строится сначала геометрический аналог функции отклика - поверхность отклика (рисунок 2). Будем для наглядности рассматривать случай с двумя факторами. В случае многих факторов геометрическая наглядность теряется, и при этом попадаем в абстрактное многомерное пространство. Приходится переходить на язык алгебры. Тем не менее, простые примеры, которые будут рассмотрены, помогут при работе со многими факторами.
Для факторов существует область определения. Это значит, что у каждого фактора есть минимальные и максимальные возможные значения, между которыми он может изменяться либо непрерывно, либо дискретно.
Пространство (или область), в пределах которого может быть представлен набор факторов, и в котором строится поверхность отклика, называется факторным пространством (рисунок 3). Оно задается координатными осями, по которым откладываются значения факторов и параметров оптимизации. Размерность факторного пространства зависит от числа факторов. При более двух факторах поверхность отклика нельзя изобразить наглядно и тогда приходится переходить на язык алгебры.
Геометрическое представление
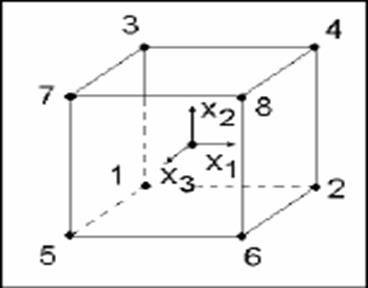 |
Рисунок 3 - Факторное пространство
После того, как рассмотрели вопрос о представлении поверхности отклика, необходимо перейти к основному вопросу: как ставить эксперимент, чтобы найти оптимум при минимуме затрат? Это, прежде всего, вопрос стратегии.
|
|
|
Во-первых. При наличии таблицы, в которой содержались бы все возможные состояния объекта и соответствующие им отклики, то отпала бы необходимость в построении математической модели. При этом было бы выбрано то состояние, которое соответствует наилучшему отклику. Но при наличии большого перебора возможных состояний мы вынуждены отказаться от практической реализации этой возможности.
Другая возможность - случайный выбор некоторого числа состояний и определение откликов в них, в надежде, что среди этих состояний окажутся оптимальное или близкое к нему состояния. Но такая интересная возможность маловероятна и не вписывается в нашу тему.
Наконец, третья возможность - строить математическую модель, чтобы с её помощью предсказывать значения откликов в тех состояниях, которые не изучались экспериментально. Если нет возможности измерить отклик в каждом состоянии, то сумеем хотя бы предсказать результат. Причем даже не в каждом состоянии, а только в наиболее интересных, в тех, которые приближаются к оптимальному значению.
Такая стратегия приводит к шаговому принципу, лежащему в основе рассматриваемого метода планирования эксперимента.
3. Шаговый принцип
За отказ от полного перебора состояний надо чем-то платить.
- Цена – это предположения, которые ставятся относительно свойств неизвестной модели до начала эксперимента (априори). Некоторые из предположений никогда не могут быть проверены. Такие предположения называются постулатами. Если в действительности предположения не выполняются, то оптимум не может быть найден. Точнее, за оптимум ошибочно принимается то, что на самом деле им не является.
- О свойствах поверхности отклика принимают следующие предположения. Главное - это непрерывность поверхности, её гладкость и наличие единственного оптимума (быть может, на границе области определения). Эти постулаты позволяют представить изучаемую функцию в виде степенного ряда в окрестности любой возможной точки факторного пространства (такие функции в математике называются аналитическими).
|
|
|
Возможно, требование непрерывности не согласуется с представлением о дискретных уровнях факторов. Это не страшно, т.к. можно считать, что фактор принимает ряд непрерывных значений (если даже некоторые значения не имеют смысла или физически нереализуемы).
На рисунке 3 изображены два варианта поиска оптимума для одной и той же поверхности. Крестиками на рисунке обозначены условия опытов. В случае «а» использован подход классический (метод Гаусса-Зейделя).
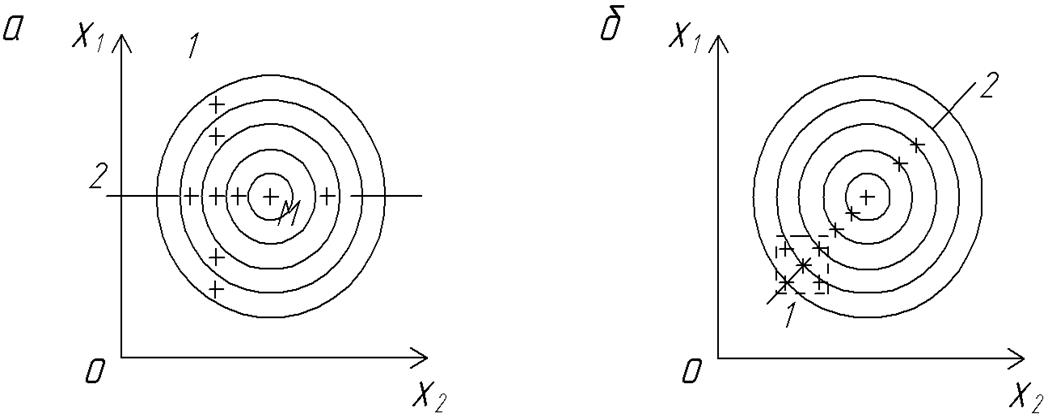
Рисунок 3 - Два способа поиска оптимума
Он состоит в том, что сначала последовательно изменяются значения одного фактора (на рисунке этот эксперимент обозначен 1). Затем находится и фиксируется наилучшее значение этого фактора. В этих условиях последовательно изменяются значения второго фактора (2) и т.д. (если больше факторов).
В случае «б» представлен простейший вариант шаговой процедуры. Сначала изучается локальная область (1), затем определяется наиболее интересное направление и в этом направлении ставятся следующие эксперименты (2).
Оказалось, что в обоих случаях достигнут одинаковый результат при сравнительно одинаковом суммарном количестве опытов. Но шаговый метод (процедура «б») в среднем эффективнее, чем процедура «а». Далее следует заняться выбором модели для первого эксперимента более конкретно.
4. Как выбрать модель?
Моделей существует много и при этом они могут быть разные. Чтобы выбрать одну из них, надо понять, что требуется от неё, т.е. необходимо сформулировать эти требования.
Главное требование к модели – это способность предсказывать направление дальнейших опытов с требуемой точностью. До получения модели неизвестно, какое направление понадобится, поэтому точность предсказания во всех возможных направлениях должна быть одинаковой. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического больше, чем на некоторую заранее заданную величину. Модель, которая удовлетворяет такому требованию, называется адекватной. Проверка выполнимости этого требования называется проверкой адекватности модели. Разработаны специальные статистические методы, с помощью которых проверяется адекватность модели.
|
|
|
Если несколько различных моделей отвечают требованиям, то необходимо выбрать самую простую. При прочих равных условиях предпочтение отдаётся степенным рядам, точнее отрезкам степенных рядов – алгебраическим полиномам. Построение полинома возможно в окрестностях любой точки факторного пространства, т.к. предполагается, что функция является аналитической. Выбрать модель – значит сравнить. А как сравнить между собой классы моделей, если свойства объекта заранее не известны? Остаётся предполагать, что должны рассматриваться такие задачи, в которых исходные постулаты окажутся верными.
Выбранные в качестве математических моделей полиномы будут различаться по максимальным степеням входящих в них переменных:
полином нулевой степени – 
полином первой степени – 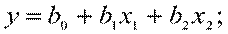
полином второй степени – 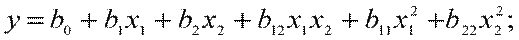
полином третьей степени – 
5. Полиномиальные модели
Итак, неизвестная функция отклика представляется полиномом. Операция замены одной функции другой эквивалентной функцией называется аппроксимацией. Значит неизвестная функция аппроксимирована полиномом. Но полиномы бывают разных степеней. Какой взять на первом шаге? Эксперимент нужен только для того, чтобы найти численные значения коэффициентов полинома. Поэтому чем больше коэффициентов, тем больше опытов окажется необходимым, но при этом преследуется цель сокращения опытов. Значит надо найти такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявленным к модели. Чем ниже степень полинома при заданном числе факторов, тем меньше в нём коэффициентов. В этой связи можно ли всегда использовать полином нулевой степени? Нет, т.к. трудно ожидать, что результаты опытов будут всегда одинаковы независимо от уровней факторов. А если результаты различны, то такая модель не будет адекватной, т.е. не будут выполняться требования.
|
|
|
Модель должна хорошо предсказывать направление наискорейшего улучшения параметра оптимизации. Такое направление называется направлением градиента. Движение в этом направлении приведёт к успеху быстрее, чем движение в любом другом направлении (это значит, что будет достигнута экономия числа опытов). Можно ли в этой связи всегда использовать полином первой степени? Да, потому что полином первой степени - линейная модель, а это то, что нужно. С одной стороны, он содержит информацию о направлении градиента, с другой – в нём минимально возможное число коэффициентов при данном числе факторов. Единственное опасение в том, что неясно, будет ли линейная модель всегда адекватной. Ответ зависит ещё и от объекта исследования.
Вопрос в том, как выбрать подобласть в факторном пространстве, чтобы линейная модель оказалась адекватной. Условие аналитичности функции отклика гарантирует эту возможность. Всегда существует такая окрестность любой точки, в которой линейная модель адекватна. Размер такой области заранее неизвестен, но адекватность можно проверять по результатам эксперимента. Значит, выбрав сначала произвольную подобласть, можно найти требуемые размеры. И как только это случится, можно воспользоваться движением по градиенту.
На следующем этапе находится линейная модель уже в другой подобласти. Цикл повторяется до тех пор, пока движение по градиенту не перестанет давать эффект. Это значит, что достигнута область, близкая к оптимуму. Такая область называется «почти стационарной». Здесь линейная модель уже не нужна. Либо попаданием в почти стационарную область задача решена, либо надо переходить к полиномам более высоких степеней, чтобы подробнее описать область оптимума. Удачный выбор подобласти имеет большое значение для успеха всей работы. Он связан с интуитивными решениями, которые принимает экспериментатор на каждом этапе.
Кроме задачи оптимизации, иногда возникает задача построения интерполяционной модели. В этом случае оптимум не интересует, т.к. результат предсказывается с требуемой точностью во всех точках некоторой заранее заданной области. Здесь не приходится выбирать подобласть. Необходимо последовательно увеличивать степень полинома до тех пор, пока модель не окажется адекватной. Если адекватной оказывается линейная или неполная квадратная модель (без членов, содержащих квадраты факторов), то её построение аналогично тому, что требуется для оптимизации.
|
|
|
Выводы
Итак, выбрана модель, которая будет систематически использоваться на первом этапе планирования эксперимента. Это алгебраический полином первой степени – линейная модель. Чтобы произвести такой выбор, понадобилось научиться изображать поверхность отклика в факторном пространстве, задаваемом прямоугольными Декартовыми координатами, по осям которых откладываются в некотором масштабе значения (уровни) факторов и значения параметра оптимизации. Поверхность отклика задана только в совместной области определения факторов. В этой области каждому возможному набору значений факторов (состоянию объекта) соответствует единственное значение параметра оптимизации. Для уменьшения размерности факторного пространства при геометрическом построении поверхности отклика можно использовать сечения.
Установлено, что математическая модель требуется для предсказания направления градиента, т.е. направления, в котором величина параметра оптимизации улучшается быстрее, чем в любом другом направлении. Такая модель позволяет избежать полного перебора состояний объекта и тем самым уменьшить количество опытов, необходимых для отыскания оптимума.
Отказ от полного перебора требует оплаты в виде предположений о свойствах поверхности отклика, которые невозможно проверить. Такие предположения выбираются по-разному. Например, можно выбрать предположения об аналитичности функции отклика и о единственности оптимума. Аналитической называется такая функция, которую можно разложить в степенной ряд в окрестностях любой точки из области её определения.
Используя эти предпосылки, можно предложить процедуру поиска оптимума, основанную на шаговом принципе. Суть принципа: проводят короткие серии опытов, по их результатам строят математическую модель, которую используют для оценки градиента, ставят новые опыты только в этом направлении. Получается циклический процесс, который заканчивается при попадании в область, близкую к оптимуму («почти стационарную» область).
Для выбора конкретной модели необходимо сформулировать конкретные требования: адекватность и простоту. Под адекватностью понимается способность модели предсказывать результаты эксперимента в некоторой области с требуемой точностью. После реализации опытов проверяется адекватность модели. Требование простоты заключается в том, что в качестве модели принимаются алгебраические полиномы, которые считаются самыми простыми. На основе накопленного исследователями опыта такие модели удовлетворяют экспериментатора. Кроме того, полином линеен относительно неизвестных коэффициентов, что упрощает обработку результатов.
После выбора класса моделей выбирают степень полинома и подобласть, в которой надо начинать эксперимент. Эти выборы связаны между собой. Однако важно, что возможен такой выбор области, при котором линейная модель окажется адекватной. Этого достаточно, чтобы оценить градиент.
Следует сказать и о задаче построения интерполяционных моделей, которые используют для предсказания откликов во всей области. Область фиксируется заранее. Необходимо последовательно повышать степень полинома, пока не найдётся адекватная модель.
|
|
|


