Перевод набранных первичных баллов в

Вариант 1.

Ответы

267,2			0,52		-0,5				0,71		-1

 

	а) 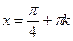, 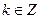; б) , .
	б)
	если , то , при остальных а нет решений
	а) Да, например, 7124 и 7119; б) нет; в) 11.

 

Решения заданий 13-19

 

Задание 13. а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

 

Содержание критерия	Баллы
Обоснованно получен правильный ответ
Получен неверный ответ из-за вычислительной ошибки и/или ошибки в отборе корней, но при этом имеется верная последовательность всех шагов решения
Решение не соответствует ни одному из критериев, приведённых выше
Максимальный балл

 

Решение.

а) Преобразуем исходное уравнение:

, .

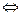
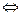
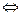
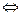
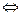
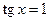
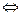
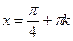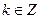б) с помощью числовой окружности отберем корни, принадлежащие отрезку . Получим корни: , .

 

Ответ: а) 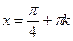, 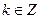; б) , .

 

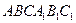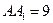Задание 14. Дана правильная призма , у которой сторона основания , боковое ребро . Точка – середина ребра , а на ребре взята точка так, что .

а) Докажите, что плоскость делит отрезок пополам.

б) Плоскость делит отрезок 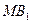на две части. Найдите длину меньшей из них.

 

Содержание критерия	Баллы
Приведено обоснованное верное доказательство в пункте а) и обоснованно получен верный ответ в пункте б)
Выполнен только пункт а) или выполнен пункт б) при отсутствии обоснования пункта а)
Решение не соответствует ни одному из критериев, приведённых выше
Максимальный балл

 

Решение.

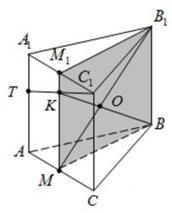
а) Отметим точку ‑ середину . Очевидно, . Проведем . Это будет прямая, содержащая среднюю линию треугольника , так как и проходит через середину . Значит, она проходит и через середину 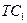(назовем ее K), что и требовалось доказать (эта точка и есть точка пересечения данных прямой и плоскости).

б) Рассмотрим плоскость . Отрезок BK лежит в ней и в плоскости , поэтому надо узнать, как отрезок BK делит отрезок ‑ диагональ прямоугольника со сторонами , . При этом .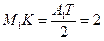

Обозначим точку пересечения BK и за O. Тогда

.

Поэтому .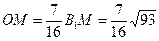

Ответ: б) .

 

Задание 15. Решите неравенство: .

Содержание критерия	Баллы
Обоснованно получен верный ответ
Обоснованно получен ответ, отличающийся от верного включением/исключением граничных точек, ИЛИ допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения.
Решение не соответствует ни одному из критериев, перечисленных выше.
Максимальный балл

 

Решение.

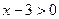Так как основание логарифмов должно быть положительным числом, то должны выполняться неравенства и . Отсюда следует, что , то есть 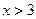. При этом условии основания логарифмов не обращаются в единицу.

Так как при 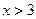оба основания больше 1, то тогда выполняется и . Тогда при 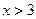получим:

.

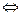
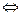
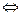
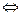
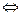
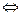
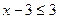
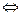
Учитывая неравенство 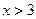, получим .

 

Ответ: .

 

Задание 16. В прямоугольном треугольнике АВС с прямым углом С точки М и N ‑ середины катетов АС и ВС соответственно, СН ‑ высота.

а) Докажите, что прямые МН и NH перпендикулярны.

б) Пусть Р ‑ точка пересечения прямых АС и NH, а Q ‑ точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН = 4 и ВН = 2.

 

Содержание критерия	Баллы
Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б)
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а), и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен
Решение не соответствует ни одному из критериев, приведённых выше
Максимальный балл

 

Решение.

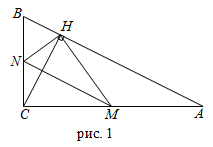
а) Треугольники АНС и ВНС прямоугольные (рис. 1), поэтому 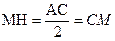и . Значит, треугольники MCN и MHN равны по трём сторонам, откуда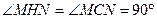

б) В прямоугольном треугольнике АВС имеем: (рис. 2).

В прямоугольных треугольниках МНР и MCQ с общим углом CMH получаем:

,

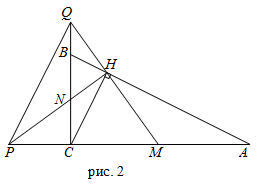
поэтому треугольники МНС и MРQ подобны с коэффициентом подобия .

Площадь S треугольника МНС равна половине площади треугольника АНС, то есть .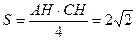

Найдём :

.

Значит, площадь треугольника MPQ равна .

 

Ответ: б) .

 

Задание 17. 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая ‑ 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

 

Содержание критерия	Баллы
Обоснованно получен верный ответ
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано
Верно построена математическая модель и решение сведено к исследованию этой модели, но при этом решение не завершено
Решение не соответствует ни одному из критериев, приведённых выше
Максимальный балл

 

Решение.

Пусть сумма кредита равна , а годовой процент составляет . Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент . После первой выплаты сумма долга составит . После второй выплаты сумма долга составит:

.

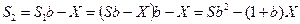После третьей выплаты сумма оставшегося долга равна

.

После четвертой выплаты сумма оставшегося долга равна

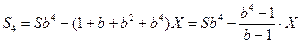
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому

.

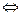
При и , получаем: и

(рублей)

Ответ: 2296350.

 

Задание 18. При каждом а решите систему уравнений

 

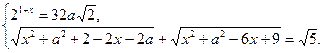
Содержание критерия	Баллы
Обоснованно получен верный ответ
Имеется правильная последовательность действий. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку.
Имеется правильная последовательность действий. Получен ответ, но решение недостаточно обоснованное ИЛИ содержит ошибки.
Решение не доведено до конца. Рассмотрены некоторые промежутки. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок.
Решение не соответствует ни одному из критериев, приведённых выше
Максимальный балл

 

Решение.

Запишем второе уравнение в виде

.

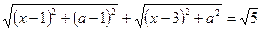Геометрический смысл уравнения состоит в том, что сумма расстояний от точки до точек и равно 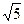. Поскольку расстояние между точками и также равно 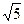, то это означает, что точка должна лежать на отрезке, соединяющем точки и . Другими словами, она удовлетворяет уравнению и условию .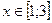

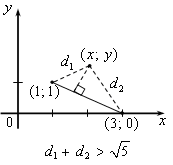
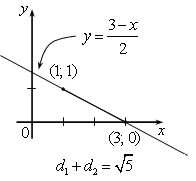
Таким образом, исходная система равносильна системе

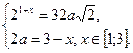
Подставив 2 а в первое уравнение, получаем

.

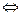
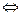
Полученное уравнение имеет очевидное решение . Поскольку функция возрастающая (как сумма двух возрастающих), то каждое значение она принимает ровно один раз. Поэтому решение ‑ единственное, ему соответствует .

Ответ: если , то , при остальных а нет решений.

 

Задание 19. Будем называть четырёхзначное число интересным, если среди четырёх цифр в его десятичной записи нет нулей, а одна из этих цифр равна сумме трёх других из них. Например, интересным является число 6321.

а) Приведите пример двух интересных четырёхзначных чисел, разность между которыми равна пяти.

б) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна 91?

в) Найдите наименьшее нечётное число, для которого не существует кратного ему интересного четырёхзначного числа.

 

Содержание критерия	Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты.
Верно получены три из перечисленных (см. критерий на 1 балл) результатов.
Верно получены два из перечисленных (см. критерий на 1 балл) результатов.
Верно получен один из следующий результатов: ‑ обоснованное решение п. а; ‑ пример в п. б; ‑ искомая оценка в п. в; ‑ пример в п. в, обеспечивающий точность предыдущей оценки.
Решение не соответствует ни одному из критериев, перечисленных выше.
Максимальный балл

Решение.

а) Примером таких чисел являются числа 7124 и 7119.

б) Предположим, что такие числа существуют. Рассмотрим какие-либо два таких интересных числа. Пусть ‑ десятичная запись большего из них, а k ‑ та из цифр a, b, c или d, которая равна сумме трёх других. Тогда сумма цифр этого числа равна 2 k, то есть чётна. Аналогично получаем, что сумма цифр меньшего из рассматриваемых интересных чисел также чётна. Так как d ≠ 0, то четвёртая цифра меньшего из рассматриваемых интересных чисел равна d − 1. Так как c − 9, либо отрицательно, либо равно 0, то третья цифра меньшего из рассматриваемых интересных чисел равна c + 1. Аналогично получаем, что вторая цифра этого числа равна b − 1. Наконец, первая цифра этого числа равна a. Значит, сумма цифр меньшего из рассматриваемых интересных чисел на единицу меньше суммы чисел большего из них. Пришли к противоречию.

в) Покажем, что искомое число равно 11. Для этого сначала приведём пример интересного четырёхзначного числа, кратного 3, 5, 7 и 9, ‑ это число 9135.

Пусть ‑ десятичная запись какого-либо интересного числа, кратного 11. Тогда

.

Получаем, что число b − a + d − c кратно 11. Поскольку a, b, c и d ‑ цифры, отсюда следует, что либо b + d = a + c, либо эти две суммы отличаются на 11. Составим две пары чисел: a и c, b и d. Пусть k ‑ та из цифр a, b, c и d, которая равна сумме трёх других, l ‑ та из них, которая в паре с k. Пусть m и n ‑ две оставшиеся из цифр a, b, c и d. Поскольку k = l + m + n, имеем k + l > m + n. Значит, k + l = m + n + 11. Вычитая из этого равенства равенство k = l + m + n, получаем l = 11 − l. Следовательно, 2 l = 11. Пришли к противоречию. Значит, не существует интересных четырёхзначных чисел, кратных 11.

 

Ответ: а) Да, например, 7124 и 7119; б) нет; в) 11.

 

Перевод набранных первичных баллов в

Поделиться:

Воспользуйтесь поиском по сайту: