Изучение формы распределения

Закономерности распределения

Закономерное изменение частот при изменении соответствующего варианта называется законом распределения.

Для правильного и для корректного выявления закономерностей нужно располагать достаточно большим объёмом совокупности, в результате реализации метода группировки закономерность распределения может проявляться более или менее отчётливо.

Закономерности распределения выражают свойства явлений и общие условия, влияющие на формирование вариации признака.

 

Пример: Распределение предприятий области по формам собственности отражают условия, определение развитие тех или иных форм на данном этапе. Эти условия выражаются: в степени разработанности законодательной базы, в структуре экономики и её состоянии в отдельных отраслях, в социальном состоянии населения, уровне квалификации занятых.

В меньшей степени для данного процесса характерно действие случайных причин, хотя полностью абстрагироваться от их проявления невозможно.

 

Изучение формы распределения

Основная задача анализа вариационных рядов – выявление закономерности распределения путём исключения влияния второстепенных, случайных для данного распределения факторов, что достигается увеличением объёма исследуемой совокупности при одновременном уменьшении интервала ряда.

Под кривой распределения понимается графическое изображение в виде непрерывной линии изменение частот в вариационном ряду, функционально связанного с изменением вариант (эмпирическая кривая).

Теоретической кривой распределения называется кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для закономерности факторов. При проведении анализа вариационных рядов целесообразно свести эмпирическое распределение к одному из хорошо исследуемых видов теоретического распределения, рассматриваемых математической статистикой. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационных рядов сводится к сопоставлению эмпирического и теоретического распределений и определению степени различий между ними.

В статистической практике встречаются разнообразные распределения. Различают следующие разновидности кривых распределения:

1. Одновершинные:

· Симметричные

· Умеренно ассиметричные

· Крайне ассиметричные

2. Многовершинные; для однородных совокупностей, как правило, характерны одновершинные распределения. Появление двух и более вершин делают необходимой перегруппировку данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагают оценку его однородности, а также показателей асимметрии и эксцесса.

Для симметричных распределений частоты двух вариант, равностоящих в обе стороны от центра распределения равны между собой. Мода и медиана таких распределений также равны.

 

а) правосторонняя As б) левосторонняя As

As > 0 As < 0

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии.

Его величина между «+» и «-».

Применение асимметрии даёт возможность определить не только величину асимметрии, но и проверить её наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной, если меньше 0,25 – незначительной.

Оценка существенности асимметрии производится на основе среднеквадратической ошибки (коэффициента асимметрии), которая зависит от числа наблюдений (объёма выборки n) и рассчитывается по формуле:

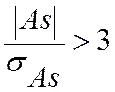- асимметрия существенна и распределение признаков в генеральной совокупности не симметрично.

Для симметричных распределений рассчитан показатель эксцесса E_k. Наиболее точно он определяется по формуле с использованием центрального момента четвёртого порядка:

На рисунках представлены два распределения островершинное и плосковершинное:

 

E_k > 0 E_k < 0

В нормальном распределении E_k = 0

Среднеквадратическая ошибка эксцесса s_Ek определяется:

n – объём выборки

Вывод: Хотя показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности их определение имеет не только описательное значение. Эксцесс и асимметрия дают определённые указания для дальнейшего исследования социально-экономических явлений. Появление значительного отрицательного эксцесса может указать на качественную неоднородность исследуемой совокупности.

Поделиться:

Воспользуйтесь поиском по сайту: