Выпуклость функции и точки перегиба

Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x₁ и x₂ из этого отрезка

Другими словами, если для любых точек x₁ и x₂ отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла.

Аналогично определяется функция вогнутая.

Определение. Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого

Определение. Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого

Так, вторая производная функции равна откуда следует, что квадратичная функция выпукла вниз на всей области определения.

Определение. Пусть функция f (x) непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда точка называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.

Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то

Достаточные условия наличия точки перегиба.

Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке Если меняет знак при переходе через точку то – точка перегиба функции f (x).

При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:

1. Найти область определения функции.

2. Определить четность или нечетность функции.

3. Найти точки пересечения графика с осями координат, если это возможно.

4. Исследовать функцию на непрерывность. Найти асимптоты графика функции.

5. Найти интервалы монотонности и точки экстремума функции.

6. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

7. Найти значение функции в нескольких дополнительных точках.

На основании полученного исследования построить график.

Пример 1. Исследовать функцию и построить ее график:

.

Решение.

1. Найдем область определения функции. Это будет вся числовая ось, кроме точек, в которых знаменатель обращается в 0.

. .

2. Функция является нечетной, т.к. , ее график симметричен относительно начала координат (значит, график можно построить только при х≥0, а затем в силу нечетности функции отобразить его симметрично относительно начала координат).

3. Точка пересечения с осями координат: - начало координат.

4. Асимптоты графика:

а) вертикальные

б) наклонные , где

.

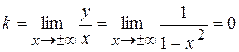-горизонтальная асимптота - ось - при .

5. Проведем полное исследование по первой производной.

Нетрудно заметить, что при любом значении области определения функции, производная , т.е. функция является всюду возрастающей. Точек экстремума нет.

8. Проведем полное исследование по второй производной.

 

при .

Выделим интервалы:

Точка является точкой перегиба графика функции . Нанесем на чертеж все полученные точки и линии

 

Задания для занятия

1. Напишите уравнение касательной к кривой у= х² в точке А(2;4).

2. Напишите уравнение касательной к кривой у= sin х в точке х=π.

3.Найдите угловой коэффициент касательной к кривой у=5 – 3 х² в точке с абсциссой х= -2.

4. Напишите уравнение нормали к кривой у²= х в точке А(8;4).

5. Напишите уравнение нормали к кривой х ² + у²= 25 в точке А(3;-4).

6. Лифт после включения движется по закону s=1,5 t²+2t+12, где s – путь в метрах, t – время в секундах. Вычислите скорость лифта в момент времени t=2.

7. Разложение некоторого химического вещества протекает в соответствии с уравнением m=m₀e^-kt, где m – количество вещества в момент времени t, k – положительная постоянная. Найдите скорость v разложения вещества и выразите ее как функцию от m.

8. Размер популяции насекомых в момент t (время выражено в днях) задается величиной p(t) = 10000 – 9000(1+t)^-1. Вычислите скорость роста популяции в момент времени t=2.

9. Найдите с помощью дифференциала приближенные значения для следующих выражений: а) , б) sin 31 °, в) ln 1,007, г)arcsin 0,51.

10. Закон накопления сухой биомассы у винограда определяется уравнением у= 0,03 х-0,0004х², где х – число дней от распускания почек, у – накопление биомассы в кг на куст. Выясните, как изменится сухая биомасса куста при изменении х от 50 до 60 дней.

11. Опытным путем установлено, что массу животного при установившемся режиме откорма можно считать функцией времени откорма t, t≥49 дней: Р=5 , где Р – масса в кг, t – время, в днях. Найдите привес животного за 10 дней, начиная с 64 –го дня кормления.

12. Урожай сахарной свеклы (т/га) в зависимости от количества вносимых минеральных удобрений (ц/га) выражается производственной функцией у= 5,4 х -2,9, где 0,6<х≤6. Подсчитайте приближенно, как изменится урожай сахарной свеклы, если количество вносимых удобрений увеличить с 4 до 6 ц/га?

13.Найдите интервалы возрастания и убывания следующих функций: а) у=3х-х³, б) у=3х+3/х+5, в) у=sin x.

14. Исследуйте на экстремум следующие функции: а) у=2х²-8, б) у=х³-9х²+15х-3, в) у=x ln x, г) у= .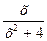

15. Найдите наименьшее и наибольшее значения следующих функций: а) у=х⁴-8х²+3 на отрезке [-2;2], б) у= на отрезке [-1/2; 1/2].

16. Найдите точки перегиба и интервалы выпуклости и вогнутости следующих кривых: а) у=2х²-8, б) у=х³-9х²+15х-3, в) у=x ln x, г) у= .

17. Проведите полное исследование функций и постройте их графики: а) у=х³-9х²+15х-3, б) у= , в) у=х³ е^-х.

 

Домашнее задание № 1 4

 

1. Напишите уравнение касательной к кривой у= 5х³ -4 в точке А(0;-4).

2. Напишите уравнение касательной к кривой у= cos х в точке х=π/2.

3. Напишите уравнение нормали к кривой х ² - у²= 9 в точке А(3; 0).

4. Зависимость количества Q вещества, получаемого в химической реакции, от времени t определяется формулой Q= a(1+b e^-kt). Определите скорость v реакции и выразите ее как функцию Q.

5. Размер популяции бактерий в момент времени t (время выражено в часах) задается формулой p(t)=10⁶+10⁴t-10³t². Найдите скорость роста популяции, когда t=1 ч.

6. Найдите с помощью дифференциала приближенные значения для следующих выражений: а) 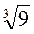, б) cos 62 °, в) ln 1,007, г)arctg 1,05.

7. Масса дрожжей в сахаре увеличивается за каждый час на 3 %. Если начальная масса равна 1 г, то после t часов роста масса равна m(t) =1,03 ^t. Найдите приближенное значение массы: а) после t=10 мин, б) после t=20 мин роста.

8. Найдите скорость изменения популяции бактерий, если в момент времени t (ч) она насчитывает p(t)=3000+100t² особей.

9. Исследуйте на экстремум следующие функции: а) у=2х-х², б) у= , в) у=(x² -1)^3/2, г) у=х+ .

10. Найдите наименьшее и наибольшее значения следующих функций: а) у=1/3 х³-2х²+3 на отрезке [-1;2], б) у=х⁴ – 2х² +3 на отрезке [-3; 2].

11. Найдите точки перегиба и интервалы выпуклости и вогнутости следующих кривых: а) у=х⁵, б) у=-х³+15х²-х-250.

12. Проведите полное исследование функций и постройте их графики: а) у=х³-9х²+15х-3, б) у= , в) у= .

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: