 |
Основная теорема метода сеток
|
|
|
|
Основная теорема теории метода сеток утверждает, что если схема устойчива, то при 
погрешность решения 
стремится к нулю с тем же порядком, что и погрешность аппроксимации:
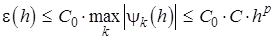, (7)
где С0 - константа устойчивости.
Неустойчивость обычно проявляется в том, что с уменьшением h решение 
при возрастании k, что легко устанавливается экспериментально с помощью просчета на последовательности сеток с уменьшающимся шагом h, h/2, h/4… Если при этом , то метод неустойчив. Таким образом, если имеется аппроксимация и схема устойчива, то, выбрав достаточно малый шаг h, можно получить решение с заданной точностью. При этом затраты на вычисления резко уменьшаются с увеличением порядка аппроксимации p, т.е. при большем p можно достичь той же точности, используя более крупный шаг h.
Виды конечно-разностных схем
Большое разнообразие методов обусловлено возможностью по-разному выбирать узлы и квадратурные формулы для аппроксимации интеграла в (4) при получении схемы (5).
Известны следующие конечно-разностные схемы:
1. Явная схема 1-го порядка (Эйлера)
2. Неявная схема 1-го порядка
. Неявная схема 2-го порядка
. Схема предиктор-корректор (Рунге-Кутта) 2-го порядка
. Многошаговые схемы Адамса
Явная схема 1-го порядка (Эйлера)
. Погрешность аппроксимации y(h) и соответственно точность (h) имеют первый порядок в силу того, что формула левых прямоугольников на интервале 
имеет погрешность второго порядка, а схема устойчива.
Неявная схема 1-го порядка
Эффективность неявной схемы заключается в том, что у нее константа устойчивости С0 значительно меньше, чем у явной схемы.
|
|
|
Неявная схема 2-го порядка
Так как формула трапеций имеет третий порядок точности на интервале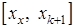 
, то погрешность аппроксимации y(h) - второй.
Схема предиктор-корректор (Рунге-Кутта) 2-го порядка
Для решения этого уравнения существует способ, при котором рассчитывают предиктор 
. При этом схема оказывается явной и имеет второй порядок.
Многошаговые схемы Адамса
При построении всех предыдущих схем для вычисления интеграла в правой части (4) использовались лишь точки в диапазоне одного шага 
. Поэтому при реализации таких схем для вычисления следующего значения 
требуется знать только одно предыдущее значение 
, т.е. рекуррентная последовательность получается первого порядка. Такие схемы называют одношаговыми. Мы, однако, видели, что для повышения точности при переходе от xk к xk+1 приходилось использовать и значения функции F внутри интервала 
. Схемы, в которых это используется (M4,M5,...), называют схемами с дробными шагами. В этих схемах повышение точности достигается за счет дополнительных затрат на вычисление функции F(x) в промежуточных точках интервала .
Идея методов Адамса заключается в том, чтобы для повышения точности использовать уже вычисленные на предыдущих шагах значения 
Список литературы
1. Синицын А.К., Навроцкий А.А. Алгоритмы вычислительной математики: учебно-метод. пособие по курсу «Основы алгоритмизации и программирования» - Мн.: БГУИР, 2007. - 80 с.
2. Синицын А. К. Практикум по курсу «Алгоритмы вычислительной математики»: учеб. пособие для студ. 1-2 го курсов всех спец. - Мн.: БГУИР, 1996.
3. Синицын А. К., Навроцкий, А. А. Алгоритмы вычислительной математики: лаб. практикум по курсу «Программирование» для студ. 1-2 го курсов всех спец. - Мн.: БГУИР, 2002.
. Самарский А.А. Теория разностных схем. - М.: Наука, 1983
. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1987
|
|
|
. Марчук Г.И. Методы вычислительной математики. - М.: Наука, 1980
. Берковский Б. М., Полевиков В. К. Вычислительный эксперимент в конвекции. - Мн: Изд-во «Университетское», 1988.
|
|
|
