 |
Анализ напряжённого состояния вала при совместном действии изгиба и кручения.
|
|
|
|
Анализ расчётной схемы вала при совместном действии изгиба с кручением.
Рассмотрим трансмиссионный вал с насаженными на него шкивами ременных передач (рис. 3.5.3, а). Под действием натяжения ремней вал кроме кручения испытывает изгиб. Схематизация силового воздействия на вал со стороны шкивов представлена на рис. 3.5.3, б.
Вращающие (скручивающие) моменты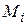 
, действующие на вал, обусловлены разностью натяжения ведущей (набегающей) 
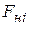и ведомой (сбегающей) 
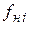ветвей ремней, надетых на шкивы. Положение вращающих моментов на расчётной схеме соответствует расположению шкивов на валу (рис. 3.5.3, в). Согласно условию равновесия вала, если трение в опорах (подшипниках) не учитывать, то при его равномерном вращении алгебраическая сумма, приложенных к нему вращающих моментов равна нулю, то есть:
 ,
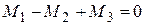| (3.5.1) |
Эпюра крутящего момента для рассматриваемой схемы представлена на рис. 3.5.3, г.
  |
Анализ напряжённого состояния вала при совместном действии изгиба и кручения.
В основе прочностного расчёта бруса, испытывающего любой вид нагружения, лежит выполнение условия прочности. В связи с этим, первой необходимостью при расчёте является определение самой опасной точки бруса с последующей оценкой в ней напряжённого состояния. В рамках простых видов нагружения в основе этих действий лежат несложные соотношения. Расчёт бруса, испытывающего совместное действие изгиба с кручением, несколько сложнее, хотя общий алгоритм остаётся неизменным.
Определение самых напряжённых точек вала требует выявления опасных сечений. С этой целью следует выполнить совместный анализ эпюры крутящего момента, э «Ткр» и эпюры суммарного изгибающего момента э «Ми». Те сечения, в которых одновременно значения крутящего и суммарного изгибающего моментов велики, являются опасными.
|
|
|
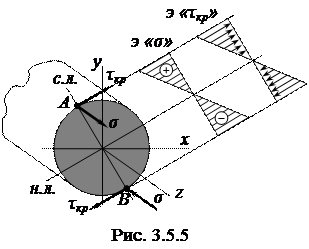Определение наиболее опасной точки сечения вала при изгибе с кручением возможно после совместного анализа эпюры касательных напряжений, обусловленных кручением, и эпюры нормальных напряжений. На рис. 3.5.5 эти эпюры представлены. Из рисунка видно, что наиболее опасными являются точки А и В, поскольку в этих точках возникают набольшие касательные и нормальные напряжения. Максимальные касательные напряжения в данном случае определяются как:
 .
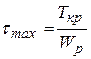| (3.5.5) |
Для определения максимальных нормальных напряжений следует воспользоваться соответствубщей формулой.
Согласно принципу независимости действия сил (принцип суперпозиций) можно выполнить анализ напряжённого состояния в точке А применительно к кручению и прямому изгибу по отдельности. Для чего следует выделить в окрестности этой точки элементарный параллелепипед (рис. 3.5.6, а). На основании теории кручения в точке А имеет место частный случай плоского напряженного состояния – чистый сдвиг. А в рамках прямого изгиба в этой точке наблюдается линейное напряжённое состояние. Соединение данных видов напряжённого состояния образовывает показанную на рис. 3.5.6, б, модель напряжённого состояния. Тогда можно предположить, что в рассматриваемой точке возникает плоское напряжённое состояние (см. рис. 3.5.6, в).
Используя аналогичный подход, можно определить вид напряжённого состояния для остальных точек сечения. Эту работу проделайте самостоятельно.
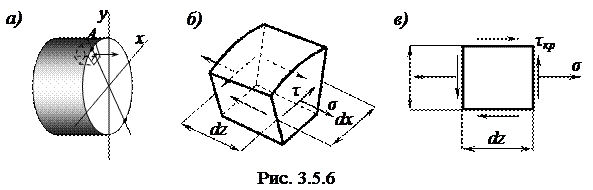Для решения проверочной задачи следует определить главные напряжения в исследуемой точке, поскольку по определению они являются экстремальными напряжениями в точке.
Если известны напряжения на двух произвольных взаимно перпендикулярных площадках, то главные напряжения можно определить по формуле
|
|
|
 ,
|
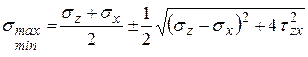Обозначения напряжений в формуле соответствуют направлению осей в рассматриваемом случае.
Так как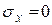 
, формула принимает следующий вид:
 ,
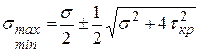| (3.5.6) |
где 
, 
.
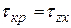Тогда:
 ,
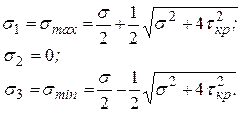| (3.5.7) |
Так как изгиб с кручением представляет собой вид сложного нагружения, оценка прочностной надёжности элемента осуществляется с помощью соответствующей теории прочности.
|
|
|
