 |
Математическая модель цикла Карно
|
|
|
|
Теоретическая часть
Идеальный тепловой двигатель
Цикл Карно, обратимый круговой процесс, в котором совершается превращение теплоты в работу. Цикл Карно состоит из последовательно чередующихся двух изотермических и адиабатических процессов.
Превращение тепла в работу сопровождается переносом определенного количества теплоты от более нагретого тела (нагревателя) к менее нагретому телу (холодильнику).
Тепловым двигателем называется машина, которая осуществляет преобразование внутренней энергии в механическую энергию.
Любой тепловой двигатель, независимо от его конструкции, состоит из трех основных частей: рабочего тела, нагревателя и холодильника.
Чем большее количество тепла будет превращаться в работу и чем меньше отдаваться холодильнику в процессе, тем эффективнее работает двигатель. Мерой эффективности работы теплового двигателя является его коэффициент полезного действия, – КПД
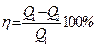. (1)
Не существует двигателя, который превращал бы в работу всё тепло полученное от нагревателя, не отдавая часть тепла холодильнику, – второе начало термодинамики.
Идеальным двигателем, позволяющим преобразовать максимальное количество тепла в работу является двигатель, работающий по циклу Карно.
КПД идеального двигателя зависит только от разности температуры нагревателя и холодильника, не зависит от устройства самого двигателя и определяется как
. (2)
Идеальный двигатель обратим. Если над рабочим телом (газом) совершать работу, то он будет передавать тепло от менее нагретого тела к более нагретому, т.е. работать как холодильная машина.
На практике идеальный двигатель будет работать бесконечно медленно, поэтому она неосуществима.
|
|
|
Повышение КПД тепловых двигателей, и приближение его к КПД идеальной машины – важнейшая техническая задача.
КПД современных паросиловых установок 
.
КПД двигателей внутреннего сгорания 
.
Анализ процесса
Если нагревать газ и позволить ему расширятся, то он может совершать работу.
Если газ охлаждать и заставить его сжиматься за счет внешнего давления, то вновь можно получит работу.
Поэтому, если попеременно, то охлаждать, то нагревать газ, помещенный в цилиндр с поршнем, то он будет работать непрерывно, и мы получим тепловой двигатель.
Если просто нагреть газ, то он расширится и совершит работу, перемещая поршень вверх. Такой процесс невыгоден, потому что, кроме совершения работы требуется еще нагревать газ.
Следовательно, нужно взять уже нагретый газ и позволить ему расширятся, при этом нагреватель не даст ему охлаждаться. Вывод: в идеальной тепловой машине нагреватель не нагревает газ, но не позволяет ему охлаждаться.
Аналогично, если взять уже охлажденный газ и позволить ему сжиматься, то можно холодильником забирать тепло, не позволяя ему нагреваться. Вывод: в идеальной машине холодильник не охлаждает газ, но не позволяет ему нагреваться.
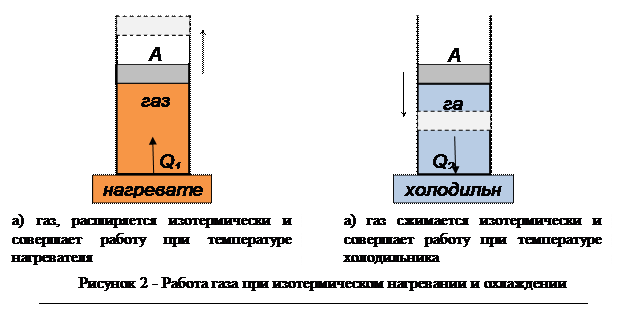
Таким образом, у нас есть два процесса для идеального двигателя: изотермическое расширение и изотермическое сжатие.
Теперь, для того чтобы соединить два полученных процесса в цикл, нужно каким-то образом, во-первых, охладить газ после изотермического расширения до температуры
холодильника и, во-вторых, нагреть газ до температуры нагревателя после изотермического сжатия. Это можно сделать, если в первом случае, позволить газу расширятся дальше адиабатически, а во втором случае, – сжиматься дальше адиабатически. Цикл Карно идеальной машины рисунок 3.
Математическая модель цикла Карно
Итак, мы узнали, что цикло Карно включает четыре технологические операции над газом: изотермическое расширение, адиабатическое расширение, изотермическое сжатие и адиабатическое сжатие. Составим математическую модель всего процесса.
|
|
|
Величины, изменение которых нас интересует это объем, давление, температура и работа. Одну из них, необходимо выбрать за независимую переменную. Будем считать независимой переменной объем газа, тогда все остальные будут функциями объема
.
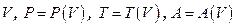Следующим шагом является выбор конструктивных параметров. Поскольку эффективность работы идеальной тепловой машины определяется температурой нагревателя и холодильника, примем за её основные параметры эти температуры:
Еще два параметра будут определять размеры нашего двигателя
.
Промежуточные объемы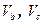 
необходимо определить.
Составим математические модели технологических процессов
1. Изотермический процесс
2. Адиабатическое расширение
.
При этом мы можем определить промежуточный объем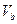 
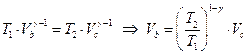
3. Изотермическое сжатие
.
4. Адиабатическое сжатие
.
При этом мы можем определить промежуточный объем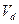 
.
.
Итак, полученные выражения образуют математическую модель цикла Карно.
Практическая часть
Используя теоретическую часть и результаты лабораторной работы №3, разработать компьютерную модель работы идеального теплового двигателя, работающего по циклу Карно.
Температуру нагревателя, холодильника и количество газа взять согласно варианту. Геометрические размеры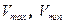 
выбрать самостоятельно. Промежуточные объемы 
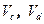рассчитать используя 
.
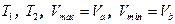Вывести результат в координатах 
, 
. Вывести график работы 
и определить работу и КПД.
Проанализировать полученные результаты, сделать выводы оформить работу.
Идеальная тепловая машина
Идеальной тепловой машиной называется устройство, преобразующее обратимо внутреннюю энергию в механическую энергию. Идеальная тепловая машина работает по циклу Карно.
Определим модельные параметры работы идеального двигателя. По условию варианта 
Зададим максимальный и минимальный объем газа, пусть
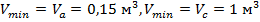
Определим 
:
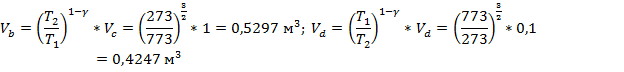
Выбираем шаг счета 
. Пусть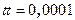 
, будем задавать изменение объема с шагом 
. Тогда максимальный объем газа составит 
|
|
|
Следовательно
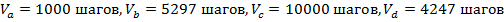
Составляем численную модель
Численная модель
1. Изотермическое расширение газа
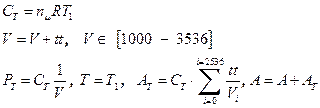
2. Адиабатическое расширение
3. Изотермическое сжатие
.
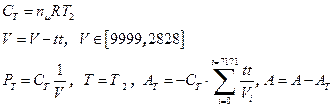4. Адиабатическое сжатие
.
Составляем программу компьютерной модели.
{Цикл Карно}
tt:=0.0001; {Шаг счета, равный шагу изменения объема}
Nm:=7; {Количество молей газа}
T1:=773; {Температура нагревателя, К}
T2:=273;{Температура холодильника}
Tk:=T1; {Начальная температура}
Va:=0.15; {Минимальный объём}
Vc:=1; {Максимальный объём}
G:=5/3; {Константа адиабаты}
Vb:=Vc*exp((G-1)*Ln(T2/T1)); {Объём в точке b}
Vd:=Va*exp((G-1)*Ln(T1/T2)); {Объём газа в точке d}
V:=Va; {Начальный объём газа, м}
A:=0;{Значение начальной работы, Дж}
{Изотермическое расширение}
PT:=0; {Давление изотермического расширения}
CT:=Nm*R0*Tk; {Константа изотермического расширения}
For i:=1500 to 3450 do
begin
V:=V+tt;
PT:=CT/V;
Tk:=Tk;
A:=A+PT*tt;
SetPixel(X0+round(V*40*MasX),Y0-round(PT*40*MasY), clBlack);
SetPixel(X0+round(V*40*MasX),Y0-round(Tk*40*MasY1), clTeal);
SetPixel(X0+round(V*40*MasX),Y0-round(A*40*MasY2), clRed);
end;
end;
{Адиабатическое расширение}
PA:=PT; {Давление адиабатического расширения}
CAT:=Tk*Exp((G-1)*Ln(V)); {Коэффициент температурный}
CAP:=PA*Exp(G*Ln(V)); {Коэффициент давления}
For i:=1 to 4000 do
begin
V:=V+tt;
PA:=CAP*Exp((-G)*Ln(V));
Tk:=CAT*exp((1-G)*Ln(V));
A:=A+PA*tt;
SetPixel(X0+round(V*40*MasX),Y0-round(PA*40*MasY), clBlack);
SetPixel(X0+round(V*40*MasX),Y0-round(Tk*40*MasY1), clTeal);
SetPixel(X0+round(V*40*MasX),Y0-round(A*40*4*MasY2), clRed);
end;
{Изотермическое сжатие}
PT:=PA;
CT:=Nm*R0*Tk; {Константа изотермического расширения }
For i:=0 to 7171 do
begin
V:=V-tt;
PT:=CT/V;
Tk:=Tk;
A:=A-PT*tt;
SetPixel(X0+round(V*40*MasX),Y0-round(PT*40*MasY), clBlack);
SetPixel(X0+round(V*40*MasX),Y0-round(Tk*40*MasY1), clTeal);
SetPixel(X0+round(V*40*MasX),Y0-round(A*40*4*MasY2), clRed);
end;
{адиабатическое сжатие}
PA:=PT;
CAT:=Tk*Exp((G-1)*Ln(V)); {Температурный коэффициент }
CAP:=PA*Exp(G*Ln(V)); {Коэффициент давления }
For i:=2000 to 3900 do
begin
V:=V-tt;
PA:=CAP*Exp((-G)*Ln(V));
Tk:=CAT*exp((1-G)*Ln(V));
A:=A-PA*tt;
SetPixel(X0+round(V*40*MasX),Y0-round(PA*40*MasY), clBlack);
SetPixel(X0+round(V*40*MasX),Y0-round(Tk*40*MasY1), clTeal);
SetPixel(X0+round(V*40*MasX),Y0-round(A*40*MasY2), clRed);
end;
End.
На рисунке 4 представлен график функции зависимости давления от объема.
На рисунке 5 – график функции зависимости температуры от объема.
На рисунке 6 – график функции работы от объема.
Как видно из графиков , процесс изменения состояния газа, действительно образует цикл, состоящий из двух изотерм и двух адиабат. Газ возвращается в первоначальное состояние.
|
|
|
Работа цикла, как это следует из графика 
, составит 
.
КПД машины.
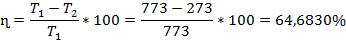
Вывод: Методом компьютерного эксперимента изучена работа идеальной тепловой машины по циклу Карно, математически вычислено КПД машины. Лабораторная работа проведена в полном объёме.
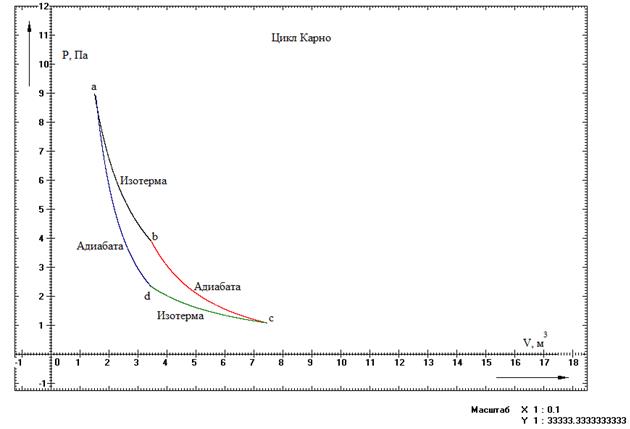
Рисунок 4 - Результат компьютерного эксперимента. Цикл Карно в координатах P=P(V)
Рисунок 5 - Результат компьютерного эксперимента. Цикл Карно в координатах T=T(V)
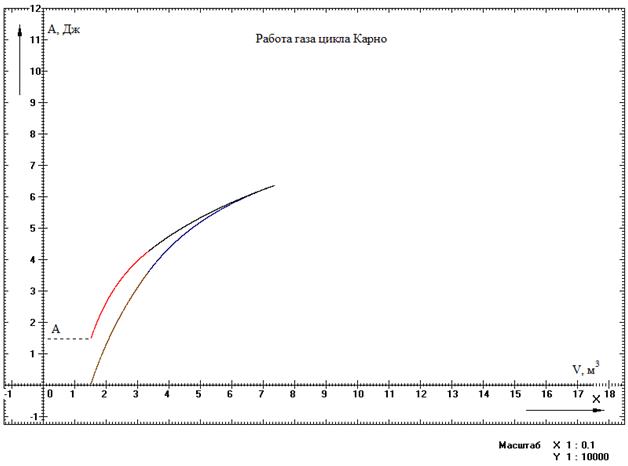
Рисунок 6 - Результат компьютерного эксперимента. Работа цикла Карно
|
|
|
