 |
Контрольная работа «Кривые и поверхности второго порядка»
|
|
|
|
1. Определение эллипса как геометрического места точек. Вывод канонического уравнения эллипса в прямоугольной декартовой системе координат. Основные параметры кривой.
2. Уравнение поверхности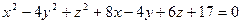 
привести к каноническому виду. Сделать рисунок в канонической системе координат. Указать название данной поверхности.
3.Составить уравнение равноосной гиперболы, если известны ее центр 
и один их фокусов 
. Сделать рисунок.
Контроль по модулю №2 «Кривые и поверхности второго порядка. Матрицы и системы линейных алгебраических уравнений»
1. Однородные системы линейных алгебраических уравнений (СЛАУ). Формы записи однородной СЛАУ. Доказательство критерия существования ненулевых решений однородной СЛАУ.
2.Решить матричное уравнение 
, где
, 
.
Сделать проверку.
3. Вычислить определитель матрицы 
. Найти обратную матрицу к .
.
4. Решить СЛАУ. Найти нормальную фундаментальную систему решений соответствующей однородной системы, частное решение неоднородной системы; записать через них общее решение данной неоднородной системы:
Вопросы для подготовки к контролям по модулям, контрольной работе, зачету и экзамену
Модуль 1
1. Геометрические векторы. Свободные векторы. Определение коллинеарных и компланарных векторов. Линейные операции над векторами и их свойства.
2. Определение линейной зависимости и линейной независимости векторов. Доказательства условий линейной зависимости 2-х и 3-х векторов.
3. Определение базиса в пространствах векторов 
, 
, 
. Доказательство теоремы о существовании и единственности разложения вектора по базису. Линейные операции над векторами, заданными своими координатами в базисе.
|
|
|
4. Определение скалярного произведения векторов, его связь с ортогональной проекцией вектора на ось. Свойства скалярного произведения, их доказательство. Вывод формулы вычисления скалярного произведения векторов в ортонормированном базисе.
5. Определение ортонормированного базиса. Связь координат вектора в ортонормированном базисе и его ортогональных проекций на векторы этого базиса. Вывод формул вычисления длины вектора, его направляющих косинусов, угла между двумя векторами в ортонормированном базисе.
6. Правые и левые тройки векторов. Определение векторного произведения векторов, его механический и геометрический смысл. Свойства векторного произведения (без док-ва). Вывод формулы вычисления векторного произведения в ортонормированном базисе.
7. Определение смешанного произведения векторов. Объем параллелепипеда и объем пирамиды, построенных на некомпланарных векторах. Условие компланарности трех векторов. Свойства смешанного произведения. Вывод формулы вычисления смешанного произведения в ортонормированном базисе.
8. Определение прямоугольной декартовой системы координат. Решение простейших задач аналитической геометрии.
9. Различные виды уравнения прямой на плоскости: векторное, параметрические, каноническое. Направляющий вектор прямой.
10. Вывод уравнения прямой, проходящей через две заданные точки.
11.Доказательство теоремы о том, что в прямоугольной декартовой системе координат на плоскости уравнение первой степени задает прямую. Определение нормального вектора прямой.
12. Уравнение с угловым коэффициентом, уравнение прямой “в отрезках”. Геометрический смысл входящих в уравнения параметров. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых, заданных своими общими или каноническими уравнениями.
13. Вывод формулы расстояния от точки до прямой на плоскости.
|
|
|
14. Доказательство теоремы о том, что в прямоугольной декартовой системе координат в пространстве уравнение первой степени задает плоскость. Общее уравнение плоскости. Определение нормального вектора плоскости. Вывод уравнения плоскости, проходящей через три заданные точки. Уравнение плоскости “в отрезках”.
15. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
16. Вывод формулы расстояния от точки до плоскости.
17. Общие уравнения прямой в пространстве. Вывод векторного, канонических и параметрических уравнений прямой в пространстве.
18. Угол между двумя прямыми в пространстве, условия параллельности и перпендикулярности двух прямых. Условия принадлежности двух прямых одной плоскости.
19. Угол между прямой и плоскостью, условия параллельности и перпендикулярности пр ямой и плоскости. Условие принадлежности прямой заданной плоскости.
20. Задача о нахождении расстояния между скрещивающимися или параллельными прямыми.
Модуль 2
21. Определение эллипса как геометрического места точек. Вывод канонического уравнения эллипса.
22. Определение гиперболы как геометрического места точек. Вывод канонического уравнения гиперболы.
23. Определение параболы как геометрического места точек. Вывод канонического уравнения параболы.
24. Определение цилиндрической поверхности. Канонические уравнения цилиндрических поверхностей 2‑го порядка.
25. Понятие поверхности вращения. Канонические уравнения поверхностей, образованных вращением эллипса, гиперболы и параболы.
26. Канонические уравнения эллипсоида и конуса. Исследование формы этих поверхностей методом сечений.
27. Канонические уравнения гиперболоидов. Исследование формы гиперболоидов методом сечений.
28. Канонические уравнения параболоидов. Исследование формы параболоидов методом сечений.
29. Понятие матрицы. Виды матриц. Равенство матриц. Линейные операции над матрицами и их свойства. Транспонирование матриц.
30. Умножение матриц. Свойства операции умножения матриц.
31. Определение обратной матрицы. Доказательство единственности обратной матрицы. Доказательство теоремы об обратной матрице произведения двух обратимых матриц.
|
|
|
32. Критерий существования обратной матрицы. Понятие присоединенной матрицы, ее связь с обратной матрицей.
33. Вывод формул Крамера для решения системы линейных уравнений с невырожденной квадратной матрицей.
34. Линейная зависимость и линейная независимость строк (столбцов) матрицы. Доказательство критерия линейной зависимости строк (столбцов).
35. Определение минора матрицы. Базисный минор. Теорема о базисном миноре (без док-ва). Доказательство ее следствия для квадратных матриц.
36. Метод окаймляющих миноров для нахождения ранга матрицы.
37. Элементарные преобразования строк (столбцов) матрицы. Нахождение обратной матрицы методом элементарных преобразований.
38. Теорема об инвариантности ранга матрицы относительно элементарных преобразований. Нахождение ранга матрицы методом элементарных преобразований.
39. Системы линейных алгебраических уравнений (СЛАУ). Различные формы записи СЛАУ. Cовместные и несовместные СЛАУ. Доказательство критерия Кронекера—Капели совместности СЛАУ.
40. Однородные системы линейных алгебраических уравнений (СЛАУ). Свойства их решений.
41. Определение фундаментальной системы решений (ФСР) однородной системы линейных алгебраических уравнений (СЛАУ). Теорема о структуре общего решения однородной СЛАУ. Построение ФСР.
42. Неоднородные системы линейных алгебраических уравнений (СЛАУ). Доказательство теоремы о структуре общего решения неоднородной СЛАУ.
|
|
|
