 |
Краткие теоретические сведения
|
|
|
|
Саратовский государственный университет
им. Н.Г. Чернышевского
КАШТАНОВ В.В.
КОММУТАЦИОННЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Учебно-методическое пособие
для студентов физического, геологического,
географического факультетов университета
Саратов 2002
ОГЛАВЛЕНИЕ
Предисловие
Краткие теоретические сведения
1.1 Общие сведения
1.2 Процессы в RL – цепи
1.2.1 Включение цепи на постоянное напряжение при нулевой начальной энергии индуктивности
1.2.2 Отключение цепи от источника постоянного напряжения
1.3 Процессы в RC – цепи
1.3.1 Включение цепи на постоянное напряжение при нулевой начальной энергии емкости
1.3.2 Отключение цепи от источника постоянного напряжения
1.4 Процессы в RLC – цепи
1.4.1 Включение цепи на постоянное напряжение при нулевой начальной энергии цепи
1.4.2 Отключение RLC – цепи от источника постоянного напряжения
Описание эксперимента
Рабочее задание
3.1 Общие сведения
3.2 Задание
Контрольные вопросы
Список литературы
Приложение
Предисловие
Учебное пособие представляет собой руководство к лабораторной работе по курсу “Основы радиоэлектроники” для студентов физических специальностей.
Целью работы является теоретическое и экспериментальное изучение переходных процессов в линейных электрических цепях на основе классического метода расчета.
В работе приводятся краткие теоретические сведения, необходимые для освоения элементов теории переходных процессов в электрических цепях, в частности – теории коммутационных переходных процессов. Рассматриваются коммутационные переходные процессы, возникающие в RL, RC, RLC – цепях. Вводятся параметры переходных процессов. Работа выполняется в соответствии с заданиями и методическими указаниями, приведенными во второй части пособия. Предусмотрено фронтальное выполнение работы на основе единой экспериментальной установки, содержащей стандартный набор электроэлементов, измерительных приборов и универсальную панель ПУЛАР-ЭР-1.
|
|
|
Краткие теоретические сведения
1.1. Общие сведения.
Переходными процессами в электрических цепях называются процессы, возникающие при переходе от одного установившегося режима к другому в результате скачкообразного изменения воздействия (его величины, формы, частоты и фазы) или параметров элементов цепей.
Такое изменение параметров источников и элементов цепей называется коммутацией.
Теоретически коммутация считается мгновенной. При наличии в цепях реактивных элементов переход от одного установившегося режима к другому никогда не происходит мгновенно. Это объясняется тем, что переход к новому установившемуся режиму связан с нарастанием или убыванием электрической 
и магнитной 
энергий в реактивных элементах. При мгновенном изменении энергии мощность
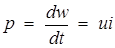
бесконечно велика, что может быть только при бесконечно больших токах и напряжениях цепи.
В данной работе рассматриваются процессы, возникающие при включении цепи под действие источника постоянного напряжения (постоянной ЭДС) и отключении цепи от источника. Такое включение и отключение цепи эквивалентно воздействию прямоугольного импульса достаточно большой длительности.
Рис. 1. Получение воздействующего импульса.
Действительно, включение в момент 
ключом 
(рис.1, а) в цепь источника постоянной ЭДС (или постоянного напряжения) эквивалентно воздействию на цепь источника 
(рис. 1,б), ЭДС которого изменяется во времени, как показано на рис. 1, в. Если ключ через время 
после включения переключается из положения 1 в положение 2, соответствующая эквивалентная ЭДС имеет вид прямоугольного импульса с амплитудой 
и длительностью , приведенного на рис. 1, г.
|
|
|
Момент включения источника, , соответствует фронту импульса; момент выключения источника, 
, - срезу импульса; промежуток времени, 
, - длительности вершины импульса.
В случае выбора длительности вершины значительно больше времени практического завершения переходного процесса 
во время вершины импульса можно исследовать процессы, возникающие при включении источника в цепь. При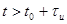 
(с момента формирования среза импульса) можно исследовать процессы в цепи при отключении источника (положение 2 ключа ).
При соизмеримости длительности импульса со временем переходного процесса (малой 
) передача импульса электрической цепью не эквивалентна процессам включения и отключения источника постоянной ЭДС, так как к концу импульса переходный процесс еще не закончен.
В этом случае в соответствии с принципом суперпозиции отклик цепи после действия прямоугольного импульса (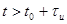) представляет собой сумму откликов на включение постоянной ЭДС (напряжения) в момент формирования фронта 
и включение постоянной ЭДС (напряжения) такой же величины, но противоположной полярности, в момент формирования среза импульса 
.
Условимся начало отсчета времени 
совмещать с моментом коммутации (или 
), т.е. считать 
.
В любой электрической цепи не могут быть бесконечно большие напряжения или бесконечно большие токи; мгновенная мощность всегда имеет конечную величину, поэтому не может иметь место мгновенное изменение накопленной в электрических и магнитных полях энергии.
Так как энергия электрического поля емкости 
связана с напряжением емкости 
как
,
а энергия магнитного поля индуктивности 
связана с ее током 
как
то это означает, что в момент коммутации напряжения на обкладках емкости и токи в индуктивностях остаются неизменными.
Сохранение в момент коммутации тока в индуктивности и напряжения на емкости неизменными составляет содержание законов коммутации.
Для расчета переходных процессов всегда необходимы начальные условия. Законы коммутации позволяют определить независимые начальные условия, соответствующие токам индуктивностей и напряжениям емкостей цепи в момент коммутации. Кроме независимых начальных условий, существуют зависимые начальные условия, соответствующие напряжениям индуктивностей, токам емкостей, напряжениям и токам активных сопротивлений и их производным по времени. Зависимые начальные условия находятся на основе уравнений цепи, определяемых по законам Кирхгофа, и независимых начальных условий.
|
|
|
Для расчета переходных процессов в электрических цепях применяются различные методы. Наиболее наглядным является классический метод расчета.
При классическом методе расчета исследуемый ток 
(напряжение 
) разделяется на две составляющие:
,
где 
- свободный ток (напряжение), действующий лишь в период установления,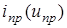 
– принужденный ток (напряжение), определяемый воздействием.
Рассчитываемый ток (или напряжение ) является полным интегралом линейного неоднородного дифференциального уравнения цепи, составленного на основе законов Кирхгофа:
является решением однородного уравнения, получаемого при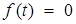 
:
,
где 
- корни характеристического уравнения;
- постоянные интегрирования;
- определяется как частное решение неоднородного уравнения.
При периодической или постоянной 
принужденный ток является установившимся током, то есть 
.
Постоянные интегрирования 
определяются на основе независимых и зависимых начальных условий.
Используем классический метод расчета для изучения переходных процессов в простых цепях, содержащих реактивные элементы.
1.2. Процессы в 
- цепи.
1.2.1.Включение цепи на постоянное напряжение при
нулевой начальной энергии в индуктивности.
Пусть в цепи (рис. 2.) ключ замыкается в момент . Приложенное напряжение равно сумме напряжения на активном сопротивлении и напряжения 
, уравновешивающего ЭДС самоиндукции 
, возникающую в индуктивности 
, поэтому уравнение цепи имеет вид:
,
,
 |
Рис. 2. Схема включения
- цепи|
|
|
где находится как частное решение дифференциального уравнения для установившегося режима, когда ЭДС самоиндукции обращается в ноль:
,
- решение однородного дифференциального уравнения:
,
,
где 
– корень характеристического уравнения;
,
; 
.
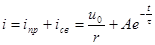Найдем постоянную интегрирования А, используя начальное условие.
До коммутации ток в индуктивности отсутствовал. По закону коммутации он не может меняться скачком, поэтому 
. Следовательно, 
; 
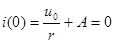Подставляя выражения А, получаем:
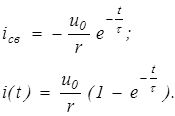
Величина 
называется постоянной времени и является промежутком времени, за который величина тока достигает 63 % величины установившегося тока для данной цепи. При 
, 
.
Подставив в формулу 
значение тока, определим напряжение на индуктивности:
При 
, поэтому в данном случае постоянная времени 
равна промежутку времени, за который напряжение индуктивности 
падает до 37% его начального напряжения 
.
Производные функций тока 
и напряжения 
,определяющие наклон касательных в начальный момент времени, имеют вид:
, 
,
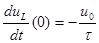поэтому соответствующие подкасательные равны постоянной времени , как показано на рис.3.
Кривые тока и напряжения для данного случая изображены на рис. 3.
 |
Рис. 3. Кривые тока и напряжения при включении - цепи.
1.2.2. Отключение -цепи от источника постоянного напряжения.
При отключении цепи, содержащей 
(рис. 4.) (
- сопротивление источника) от источника электрической энергии на индуктивности возникает ЭДС самоиндукции 
.
 |
Рис. 4. Схема отключения – цепи.
Пусть ключ размыкается в момент 
. При отсутствии внешнего источника напряжения сумма падений напряжения на элементах цепи, образовавшиеся после размыкания ключа К, равна нулю.
Уравнение для тока цепи iпр и iсв, имеют вид:
Постоянная интегрированя Аопределяется из начального условия:
так как к моменту размыкания ключа в – цепи протекал постоянный ток.
где 
постоянная времени этой цепи.
Подставив в формулу 
значение из предыдущего выражения, определим напряжение на индуктивности:
Кривые тока и напряжения при отключение цепи от источника постоянного напряжения изображены на рис. 5.
 |
Рис. 5 Кривые тока и напряжения при отключении – цепи.
I.3. Процессы в 
– цепи.
11.3.1. Включение цепи на постоянное напряжение при
нулевой начальной энергии емкости
Пусть в цепи (рис. 6) ключ замыкается в момент .
 |
Рис. 6. Схема включения – цепи.
Для цепи, образующейся после коммутации, справедливы уравнения:
|
|
|
Так как -цепь подключается к постоянному напряжению 
, 
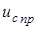- равно установившемуся напряжению емкости, когда ток переходного процесса в цепи прекращается. Переходное напряжение на емкости находится из следующих уравнений:
В начальный момент, когда 
, ёмкость разряжена. По закону коммутации напряжение на емкости не может изменяться скачком, поэтому 
и
Подставив в формулу тока емкости найденное выражение 
, получим:
; 
Кривые тока и напряжения, получаемые при включении цепи на постоянное напряжение, изображены на рис.7.
 |
Рис.7. Кривые тока и напряжения при включении цепи.
1.3.2. Отключение цепи от источника постоянного напряжения
Пусть в цепи (рис. 8) ключ размыкается в момент 
Внешний источник напряжения после коммутации в цепи отсутствует, поэтому сумма напряжений на элементах цепи в контуре, образующемся после размыкания ключа К, равна нулю.
Уравнение для переходного напряжения емкости имеет вид:
.
 |
Рис. 8. Схема отключения -цепи.
Внешнее воздействие в цепи отсутствует, уравнение цепи – однородное, поэтому
До размыкания ключа емкость была заряжена до напряжения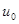 
, поэтому по закону коммутации постоянную 
находим из начального условия 
. При 
и
,
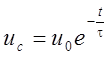где 
-постоянная времени этой цепи.
Кривые тока и напряжения при отключении источника постоянного напряжения от цепи изображены на рис. 9
 |
Рис. 9. Кривые тока и напряжения при отключении -цепи.
Таким образом, в рассмотренных цепях напряжения и токи во время переходного процесса изменяются либо по экспоненциальному закону, либо по закону 
.
Постоянная времени цепи 
характеризует скорость переходного процесса.
За время 
убывающая по экспоненте величина тока или напряжения уменьшается в 
раз и приближается к 0,37 своего первоначального значения, а нарастающая по закону – приближается к 0,63 установившегося значения.
За время 
и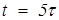 
убывающая величина достигает соответственно около 0,05 и 0,01 первоначального значения, нарастающая – около 0,95 и 0,99 установившегося значения.
Практически переходный процесс считается законченным за время 
.
I.4. Процессы в 
цепи.
1.4.1. Включение цепи на постоянное напряжение
при нулевой начальной энергии
Пусть в цепи (рис.10) ключ замыкается в момент .
 |
Рис.10. Схема включения -цепи.
Для этой цепи уравнение Кирхгофа имеет вид:
Дифференцируя это соотношение, получим уравнение, определяющее свободный ток:
,
или, обозначив
получим: 
Характеристическое уравнение
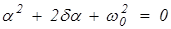
имеет два корня:
;
или
Таким образом,
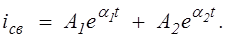
В связи с тем, что воздействующее на цепь напряжение имеет постоянную величину, установившийся ток также должен быть постоянным током, не пропускаемым емкостью 
. Поэтому ток установившегося режима будет равен 0, т.е. 
; следовательно,
Начальные условия:
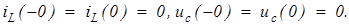
Учитывая начальное условие для тока, имеем:
Из интегродифференциального уравнения цепи при 
и 
, находим:
.
Определяем произвольные постоянные 
и 
:
Таким образом,
Характер переходного процесса при заряде емкости оказывается существенно различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными.
Рассмотрим возможные случаи.
1. Корни характеристического уравнения вещественны и отличны друг от друга. Это возможно при условии 
, т.е. 
или 
. Примем 
.
Так как 
, 
, то при изменении 
от 
до 
величины 
и 
убывают от 1 до 0 и разность 
всегда положительна. Следовательно, ток не меняет своего направления – емкость заряжается монотонно. Напряжение на емкости при заряде изменяется от 0 до конечного значения 
(рис.11). В данном случае процесс будет апериодическим без изменения направления тока.
Рис.11. Кривые тока и напряжения при включении в апериодическом режиме.
2. Корни характеристического уравнения вещественны и равны друг другу. Это имеет место при условии 
, т.е. при 
. Характер процесса не отличается от рассмотренного выше случая, когда . Процесс тоже апериодический.
Данный случай при является предельным случаем апериодического заряда, так как при дальнейшем уменьшении 
ниже значения 
заряд становиться колебательным.
3. Пусть корни характеристического уравнения являются комплексными, 
, т.е. 
.
Введем обозначение 
. Корни характеристического уравнения перепишем в виде:
Для тока и напряжения емкости имеем:
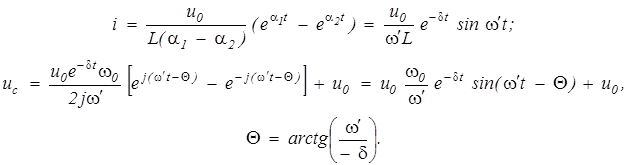
Из полученных выражений видно, что процесс в данном случае является коле
бательным. Ток, затухая, периодически изменяет знак. Напряжение емкости имеет затухающие колебания относительно напряжения источника как показано на рис.12.
 |
Рис.12. Кривые тока и напряжения при
включении - цепи в колебательном режиме.
1.4.2. Отключение цепи от источника постоянного напряжения.
При отключении цепи от источника постоянного напряжения (рис.13) характер переходного процесса зависит от того, будут ли корни характеристического уравнения вещественными 
или комплексными 
.
 |
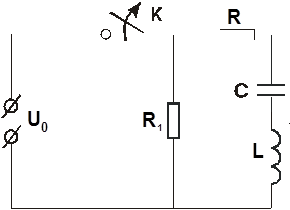Рис 13. Схема отключения RLC - цепи
Законы изменения тока в случае отключения и включения цепи аналогичны, токи отличаются в этих случаях только знаками, а напряжение при отключении цепи от источника, т.е. при разряде емкости, изменяется от начального значения до 0.
 |
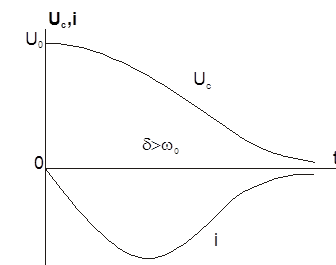Кривые апериодического разряда емкости представлены на рис. 14.,
Рис.14. Кривые тока и напряжения при
отключении - цепи в апериодическом режиме.
Кривые колебательного разряда емкости - на рис. 15.
 |
Рис.15.Кривые тока и напряжения при
отключении - цепи в колебательном режиме.
Скорость затухания колебательного переходного процесса зависит от величины 
, имеющей размерность времени. За время 
амплитуда колебаний уменьшается в раз, т.е. до 0,37 ее начального значения. Практически колебательный переходный процесс считается законченым за время 
.
Описание эксперимента
В качестве входного сигнала, обеспечивающего имитацию замыкающей и размыкающей коммутации, при экспериментальных исследованиях используются колебания типа ''меандр'', представляющие собой периодические прямоугольные импульсы с паузой между импульсами, равной их длительности.
В экспериментальных установке могут использоваться как генераторы, непосредственно формирующие ''меандр'' (например ГЗ-112), так и генераторы синусоидальных колебаний. В первом случае импульсы генератора подаются прямо на вход исследуемой цепи. Для второго случая схема установки с формирователем универсальной панели ПУЛАР-ЭР-1 приведена на рис. 16. Формирователь импульсов преобразует синусоидальные колебания в периодически повторяющиеся импульсы, приближающиеся по форме к колебаниям типа ''меандр'', с частотой повторения 
, равной частоте синусоидальных колебаний.
 |
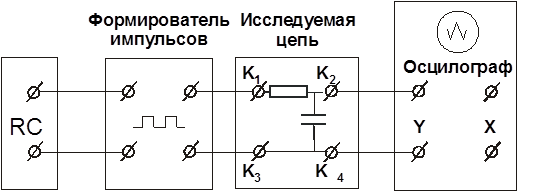Рис. 16. Общая схема экспериментальной установки.
Длительность фронта и среза импульсов значительно меньше длительности вершины, поэтому форму импульсов можно считать практически прямоугольной.
Импульсы формирователя подводятся к исследуемой цепи, позволяя исследовать процессы при включении постоянного и импульсного напряжения.
Наблюдение кривых, характеризующих переходные процессы в цепях, осуществляется с помощью электронного осциллографа, подключенного к элементу цепи, напряжение или ток которого исследуются.
Рабочее задание
3.1. Общие сведения
Вход исследуемой схемы соединяют с клеммами 
на универсальной панели. Выходной элемент схемы, форма напряжения на котором исследуется осциллографом, соединяют с общей (корпусной) точкой схемы (клемма 
), как это показано на рисунках к заданию.
Для подачи на входные клеммы прямоугольного напряжения выход генератора сигналов ГЗ – 7А (0-30 В; 1000 Ом) или генератора другого типа с аналогичными параметрами коаксиальным кабелем соединяют с клеммами 
, обозначенными ∏, и нажимают правую кнопку с таким же обозначением. Ручками регулировки выхода генератора ''грубо'', ''плавно'' устанавливают по вольтметру на его лицевой панели выходное напряжение 30 В. Величины емкостей конденсаторов, сопротивлений резисторов и секции катушек, соответствующие заданию, приведены в таблице 1.
Индуктивности секций катушек:
| Секция | 1 - 5 | 1 - 6 | 1 - 7 | 1 - 8 |
| Индуктивность, mГн |
Частота колебаний генератора сигналов 
, устанавливается в соответствии с заданной (расчетной) длительностью импульса 
:
,
и уточняется путем измерений с помощью осциллографа ( в небольших пределах зависит от величины амплитуды выходного напряжения генератора сигналов).
В работе необходимо экспериментально исследовать токи и напряжения цепей, приведенных на рис.17, при передаче импульсов большой длительности, превышающей время практического завершения переходного процесса 
, что эквивалентно включению и отключению источника постоянной ЭДС (постоянного напряжения), а также импульсов малой длительности, соизмеримой с постоянной времени 
или интервалом времени 
.
 |
 |
Рис.17. Экспериментальные цепи
3.2. Задание
Номер задания указывает преподаватель. Параметры элементов цепей, соответствующие заданному номеру, приведены в таблице 1.
1. Рассчитать и собрать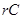 
- цепи:
а) с постоянными времени, значительно меньшими длительности импульсов;
б) с постоянными времени, соизмеримыми с длительностью импульсов. Сопротивлением генератора пренебречь.
2. Получить на экране осциллографа кривые напряжения и токов для случаев а) и б) п.1. Объяснить их, используя принцип суперпозиции.
3. Определить по экспериментальным осциллограммам постоянные времени исследуемых -цепей. Провести сравнения с расчетом.
4. Исследовать передачу импульсов малой длительности цепями, приведенными на рис. 17а и, используя принцип суперпозиции, объяснить ее по результатам, полученным по п.1-3.
5. Провести исследования 
- цепей (рис. 17б), соответствующие заданиям п. 1-3 для - цепей.
6. Исследовать передачу импульсов малой длительности -цепями, приведенными на рис.17б. Используя принцип суперпозиции, объяснить ее по результатам, полученным по п.5.
7. Рассчитать и собрать 
- цепи:
а) с временем апериодических и колебательных переходных процессов меньше длительности импульсов,
б) с временем апериодических и колебательных переходных процессов, не заканчивающихся за время, равное длительности импульсов .
Для колебательного процесса с временем 
(п. 7а)принять 
.
Для колебательного процесса с временем , соизмеримым с длительностью импульса
