 |
Расчет режима кольцевой сети.
|
|
|
|
Расчет режима радиальной сети
Рассмотрим расчет режима радиальной сети, т.е. состоящей из нескольких последовательно соединенных участков.
Расчет по данным конца n-го участка
Пусть ( Заданы 
, 
), т.е известны напряжение и мощность в конце
n-го участка.
Совместим 
с действительной осью 
,.
, совместим с действительной осью 
, 
и выполним расчет (n-1) участка.
Векторная диаграмма имеет вид:
Результирующий угол сдвига векторов 
.
В процессе расчета вектор напряжения в конце каждого участка совмещаем с действительной осью, в этом случае 
не будет комплексным числом.
Расчет режима радиальной сети при задании модуля напряжения в начале и мощностей нагрузок в узлах.
Расчет режима выполняется в два этапа
I этап.
Примем, что модули напряжений во всех узлах одинаковы: 
Определим потери на каждом из участков:
Тогда в начале первого участка получим:
,
(при этом мощность вначале посчитана не корректно).
II этап
Определяем последовательно падение 
и потери напряжения 
на всех участках (начиная с первого, где известны напряжение и мощность).
Расчет режима кольцевой сети.
При расчете кольцевая сеть представляется как сеть с двухсторонним питанием, если разрезать ее в центре питания (ЦП).
Известны мощности в узлах 
и напряжение в центре питания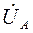 
.
Произвольно зададим направления потоков мощности на участках.
- замкнутый контур в нем 
.
В соответствии со II Законом Кирхгофа получим:
.
Примем допущение 1) 
2) 
Напомним 
, т.е. 
. Тогда:
.
(1) 
.
Пренебрегая потерями мощности на участках сети, воспользуемся
|
|
|
I Законом Кирхгофа в форме баланса мощностей и выразим мощности 
через мощность 
и через мощности 
.
Выражение (1) приобретает вид:
Откуда:
,.
Данное выражение называют правилом моментов.
7.
Если линию представить балкой, закрепленной одним концом в стене и представить, что мощность -это сила, а сопротивление –плечо. то можно записать сумму моментов (приняв за положительное направление против часовой стрелки:
Аналогично для 
,
Поскольку принято допущение об отсутствии потерь мощности на участках сети (
), то 
Поскольку данное решение получено еще и в предположении 
, т.е не учитываются потери напряжения на участках сети, то истинное потокораспределение будет отличаться от него тем сильнее, чем менее справедливы принятые допущения.
Таким образом, найденное решение не является окончательным и подлежит уточнению.
Выделим в начале точку потокораздела, т.е. узел, к которому мощность подходит с двух сторон. (в данном случае это будет узел 2) и представим кольцевую сеть в виде двух радиальных сетей.
Отметим, что в общем случае точки потокораздела по активной и реактивной мощностям могут не совпадать ( тогда целесообразно за точку потокораздела принять точку потокораздела по активной мощности, соответственно поменяв знак реактивной мощности на смежном участке сети)
Итак, получаем 2 радиальные сети, каждая из которых состоит из двух участков, для каждой из которых известны мощности нагрузок в узлах и напряжение в ЦП.
Расчет режима такой радиальной сети описан выше.
В результате расчета режимов каждой из сетей мы найдем модули напряжений 
и 
.Если 
(**), т.е. выполняется заданная точность расчета по напряжению и можно принять, что напряжение в узле 2 равно 
.
Если же неравенство не выполняется, то корректируем потокораспределение, найденное по правилу моментов, введя уравнительный ток 
и уравнительную мощность 
.
|
|
|
, 
, 
- сумма сопротивлений участков сети.
Например, когда 
, т.е. 
, то 
, 
Найдя значение 
, 
необходимо ввести новое значение уравнительной мощности и повторить расчет.
Чаще это приходиться делать для кольцевых сетей 
.
Итак, этапы расчета режима кольцевой сети:
- Предварительный расчет по правилу моментов
(в предположении, что 
, 
, 
).
- На основании предварительного расчета определяется точка потокораздела
- Кольцевую сеть условно разделяют в точке потокораздела и рассчитывают режимы двух радиальных сетей.
Если найденные значения напряжений в точке потокораздела, отвечают заданной точности расчета, то расчет закончен.
Если нет, то определяют уравнительный ток и мощность.
Далее корректируются найденные на первом этапе значения
и 
, вычисляются значения 
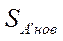и 
.
Затем повторяется расчет режима каждой радиальной сети.
Проверяем условие (**). Если это условие не выполняется, вводим новое значение 
и 
.
|
|
|
