Обыкновенные д.у. первого порядка. Ур-я с разд-ся пер-ми. Линейные д.у. Обыкновенные д.у. первого порядка

Метрические пространства. Полные метрич. пр-тва

Опр1. Метрическим пространством называются пара (Х, r), состоящая из некоторого множества (пространства) X элементов (точек) и расстояния, т.е. однозначной, неотрицательной, действительной функции r(х,у), определенной для любых x,уÎX, называемой расстоянием или метрикой,и подчиненной следующим трем условиям (аксиомам):

1) r (x,y) =0 Û x = y,

2) (аксиома симметрии): r (х,у) = r (у,х),

3) (аксиома треугольника): r (х,у)≤r (x,z) + r (z,y).

Опр2. Множества всех xÎX, удовлетворяющих неравенству r(х, )=r, называется открытым шаром с центром в точке радиуса r. А открытый шар r(х,х₀)< называется -окрестностью точки х₀.

Опр3. Точка х₀ ÎX называется пределом последовательности (х_п), если для любого >0 сущ-ет n₀ÎN такое, что при всех п>n₀ выполняется неравенство r (х_п, х₀)< (т.е. все члены последовательности при п>n₀ находятся в -окрестности точки х₀). При выполнении опр3 говорят, что последовательность (х_п) сходится, и пишут .

Опр4. Последовательность (х_п) называется фундаментальной, если удовлетворяет условию Коши, т.е. для любого >0 сущ-ет n₀ÎN такое, что при всех п>n₀ и m>n₀ выполняется неравенство r (х_п, х_m)< .

Всякая сходящаяся последовательность является фундаментальной. Обратное имеет место не всегда.

Опр5. Если метр-е пр-тво Х таково, что в нем всякая послед-ть сх-ся, то это пр-тво наз-ся полным.

 

Принцип сжимающих отображений

Опр1. Говорят, что отображение А:М→М имеет неподвижную точку х₀, если А х₀ = х₀.

Опр2. Отображение f метр-го пр-тва Х в себя наз-ся сжимающим, если сущ-ет 0<α<1 такое, что для любых x,yÎX вып-ся нер-тво r (f(х),f(у)) ≤ α r(х_п, y) (1).

Всякое сжимающее отображение является непрерывным. Действительно, х_п → х, r(х,n)→0, то r(f(х),f(у)) ≤ αr(х_п,х)→0 согласно (1).

Т (Банах). Всякое сжимающее отображение, определенное в полном метр-ом пр-тве, им. одну и только одну неподвижную точку (т.е. Ур-е f(x)=x им. ед-е реш-е).

Д. Сущ-ет х₀ –произв. т-ка метр-го пр-тва Х. положим , , . Получаем посл-ть , где . Рассмотрим (2).

Т.к. 0<α<1, то и выражение (2) при достаточно большом n является как угодно малым. Этим док-ли, что посл-ть фундаментальна. По условию, Х-пр-тво явл-ся полным, значит сущ-ет . А т.к. отображение f явл-ся непрерывным, то , т.е. . Т.обр. док-но сущ-ние неподв-ой т-ки. Осталось док-ть ее ед-ть. Пусть и , тогда ; (т.к. ) .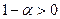

Принцип сжим-х отбр-ий широко исп-ся при док-тве теорем. Одновременно с док-твом он дает приближенный м-д нах-я реш-я (м-д последовательных приближений). Продемонстрируем применение этой теоремы на примере задачи о сущ-ии и ед-ти решения д.у. (3) с начальными условиями . Эта задача есть задача сущ-я и ед-ти неподвижной точки отобр-я (4). Функция предполагается непрерывной в области и в этой обл-ти уд-ет условию Липшица , где к – постоянная. Точка внутренняя точка . Отображение (4) определено в метрическом пр-тве всех непрерывных ф-ий на . Это пр-тво полное; остается выяснить, при каких условиях оператор А явл-ся сжимающим. Если усл-е Липшица выполнено, то мы будем иметь при любом t из : и, следовательно, . Тогда при условии , оператор А является сжимающим и теорема Банаха м.б. применена.

 

Обыкновенные д.у. первого порядка. Ур-я с разд-ся пер-ми. Линейные д.у. Обыкновенные д.у. первого порядка

Обыкновенным д.у. наз-ся ур-е, связывающее незав-ю пер-ю, неизв-ю ф-цию этой пер-ой и ее производные различных порядков. Порядком д.у. наз-ся наивысший порядок входящих в него производных. Общий вид обык-го д.у. n -го порядка: , где F нек-я функция (n+2) пер-х.

Опр. Всякая функция у = у(х), при подстановке которой обыкн-е д.у. обращается в тождество, называется решением этого д.у.

Всякое обыкновенное д.у. имеет бесконечное множество решений. Для обыкновенного д.у. п -го порядка сущ-ет реш-е, содержащее п произв-х пост-х. Такое реш-е наз-ся общим решением. Придавая произвольным пост-м общего реш-я различные числовые значения, будем получать частные решения д.у. Частное решение д.у. не содержит произв-х пост-х.

Операцию нахождения решений д.у. называют интегрированием д.у. Взятие интеграла будем называть квадратурой. Общее решение д.у., особенно если оно записано в неявной форме, часто называют общим интегралом.

График решения д.у. называют интегральной кривой этого д.у.

Пусть д.у. первого порядка задано в виде , где определена в нек-ой области G. Это ур-е ставит в соот-е каждой точке (x,y)ÎG опред-е значение у'. Иначе говоря, ур-е (1) задает в каждой точке области Gнек-ое направление, совпадающее с направлением касательной к интегральной кривой, проходящей через эту точку. Совокупность этих направлений называется полем направлений ур-я (1). Для наглядного изображения поля направлений в каждой точке области G проводят отрезок с угловым коэф-ом у'.

При построении поля направлений удобно рассм-ть геом-е места точек, в к-ых у' имеет пост-е значение. Мн-ва таких т-к наз-ют изоклинами.

Начальные условия

Пусть дано ур-е первого пор-ка . Ее общее реш-е содержит одну произвольную пост-ую: . Часто треб-ся найти то частное реш-е, к-е при х=х₀ принимает знач-е у=у₀. Эти условия наз-ся нач-ми условиями. Чтобы удовлетворить начальным условиям, нужно определить соответствующее знач-е пост-ой . Нач-е усл-я записывают: или .

Частное реш-е, удовл-ее нач. усл-ям, наз. реш-ем с нач. усл-ми. Ему соответствует интегральна кривая, проходящая через точку .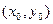

Общее реш-е д.у. n -го порядка содержит n произвольных пост-ых: . Их можно найти, если иметь n условий , ,…, . Соответствующие знач-я пост-ых нах-им из сисетмы

Задачу нах-ия реш-ия у = у(х) д.у. , удовл-го нач. усл-ям , наз-ют задачей Коши (анал-но и для д.у. порядка k, k>1).

Поделиться:

Воспользуйтесь поиском по сайту: