Получение математической модели графоаналитическим методом

Лабораторная работа №5. «Идентификация динамических характеристик объектов»

Цели и задачи работы

В лабораторной работе приводятся теоретические основы и методика получения математических моделей объектов автоматического управления. Рассмотрены случаи объектов с самовыравниванием и без самовыравнивания и методы проверки адекватности.

Объектом исследования в лабораторном практикуме является кожухотрубный теплообменник. Цель функционирования объекта – поддержание заданной температуры подогреваемой воды.

Упрощенная схема объекта показана на рисунке 5.1, где обозначены:

- U – управляющее воздействие (вход) – расход пара;

- X – регулируемый параметр (выход) – температура горячей воды;

- X1 – промежуточный (вспомогательный) режимный параметр – расход пара;

- V – возмущение – расход холодной воды.

Рисунок 5.1 – Объект исследования

 

Содержание работы. Теоретические основы

Графоаналитический метод

Во многих случаях для определения передаточной функции систему можно использовать запись её переходной функции. Такой способ, применим к большинству типов линейных систем, а именно к системам первого и второго порядков и к апериодическим системам высшего порядка.

Наиболее корректно графический метод идентификации с использованием переходных функций применяется к процессам первого порядка.

Переходная функция системы первого порядка имеет вид:

(5.1)

или в форме преобразования Лапласа

, (5.2)

где есть передаточная функция системы первого порядка, а Y(s) = 1/s = L[единичная ступенька] является изображением ступенчатого входного сигнала. Видно, что при t = T функция x(t) равна: .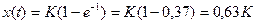

Постоянная времени Т системы первого порядка равна отрезку времени, за которое переходная функция достигает 63% своей установившейся величины. Коэффициент К (обычно имеющий размерность) представляет собой соотношение между установившейся величиной выходного сигнала системы и амплитудой входа.

Постоянную времени можно определить по-другому, если провести касательную к переходной функции на начальном участке (при t = 0) до точки пересечения с уровнем установившейся величины сигнала. Точка пересечения соответствует времени Т с момента подачи входного воздействия, так как наклон кривой х при t = 0 равен:

. (5.3)

Изменение наклона во времени выражается следующим образом:

. При t = T наклон достигает величины К.

5.3 Оборудование, технические и инструментальные средства

Для выполнения работы необходим персональный компьютер с установленной операционной системой MsWindows. Используются программы для ПК «ЛАБ5. Виртуальная лабораторная работа №5 по дисциплине МИОУ. Исследование динамики объектов управления» и «Оценивание состояния системы дискретным фильтром Калмана»

 

Описание хода выполнения работы. Исходные данные.

Исследование главного канала регулирования

5.4.1.1 Снятие динамических характеристик объекта

Таблица 5.1 – Результаты эксперимента – главный канал регулирования

Время - t	Выход - X	ΔX
	63.135
	63.135	0.274
	63.135	0.743
	63.726	1.392
		2.398
	64.469	2.96
	65.118	3.226
	66.124	3.69
	66.686	3.772
	66.952	3.891
	67.416	3.993
	67.498	4.089
	67.617	4.107
	67.719	4.168
	67.815	4.224
	67.833	4.272
	67.894	4.3
	67.95	4.352
	67.998	4.371
	68.026	4.412
	68.078	4.422
	68.097	4.432
	68.138	4.435
	68.148	4.437
	68.158	4.438
	68.161	4.44
	68.163	4.441
	68.164	4.442
	68.166	4.442
	68,168	5,033

Получение математической модели графоаналитическим методом

Исходная кривая разгона аппроксимируется переходным процессом в апериодическом звене первого порядка с передаточной функцией и переходным процессом для t ≥ τ.

Таблица 5.2 – Данные необходимые для построения модели кривой разгона

τ	T	С	ΔU
	10,5	0,5032

Переходный процесс примет вид .

В простейшем случае для проверки адекватности полученной математической модели можно воспользоваться формулой:

(5.26)

Величина не должна превышать 3-7%.

Рисунок 5.2 – Результаты проверки адекватности – главный канал регулирования (графоаналитический метод)

Поделиться:

Воспользуйтесь поиском по сайту: