Метод эквивалентного генератора

Оглавление

1 Краткие теоретические сведения. 4

1.1 Закон Ома. 4

1.2 Обобщенный закон Ома. 4

1.3 Взаимные преобразования звезды и треугольника сопротивлений 5

1.4 Законы Кирхгофа. 6

Пример 1. 7

1.5 Метод контурных токов. 8

Пример 2. 9

1.6 Метод узловых потенциалов. 11

Пример 3. 12

1.7 Метод эквивалентного генератора. 14

Пример 3. 15

1.8 Потенциальная диаграмма. 19

Пример 4. 19

2 Задание. 22

3 Библиографический список. 35

Краткие теоретические сведения

Закон Ома

Закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока без активных элементов (рис.1.1):

;

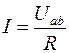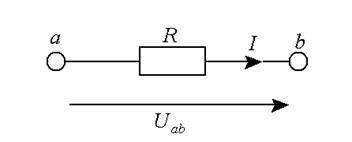
Рис.1.1

Обобщенный закон Ома

Обобщенный закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока, содержащем резистор и идеальный источник ЭДС (рис.1.2):

;

Формула справедлива для указанных на рис.1.2 положительных направлений падения напряжения на участке цепи (U_ab), идеального источника ЭДС (Е) и положительного направления тока (I).

 

Рис.1.2

Взаимные преобразования звезды и треугольника сопротивлений

В сложных цепях встречаются соединения, которые нельзя отнести ни к последовательным, ни к параллельным. К таким соединениям относятся трехлучевая звезда и треугольник сопротивлений (рис.1.3). Их взаимное эквивалентное преобразование во многих случаях позволяет упростить схему и свести ее к схеме смешанного (параллельного и последовательного) соединения сопротивлений. При этом необходимо определенным образом пересчитать сопротивления элементов звезды или треугольника.

 

 

 

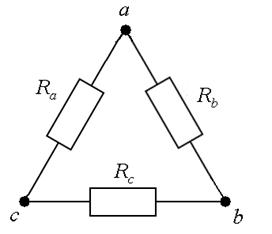
Рис.1.3

 

Формулы эквивалентного преобразования треугольника сопротивлений трехлучевую звезду:

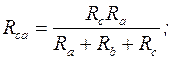
Формулы эквивалентного преобразования трехлучевой звезды сопротивлений в треугольник:

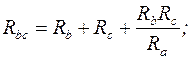
Законы Кирхгофа

Режимы электрических цепей определяются первым и вторым законами Кирхгофа.

Первый закон Кирхгофа для цепи постоянного тока:

Алгебраическая сумма токов в узле равна 0.

;

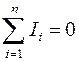Второй закон Кирхгофа для цепи постоянного тока:

Алгебраическая сумма падений напряжений на элементах контура равна алгебраической сумме ЭДС, действующих в этом же контуре.

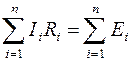
Для составления системы уравнений на основании законов Кирхгофа необходимо:

1. Выбрать произвольно положительные направления искомых токов ветвей и обозначить их на схеме. Число токов должно быть равно числу ветвей схемы (В). Составить (Y - 1) – уравнений по первому закону Кирхгофа, где (Y) – число узлов схемы. Со знаком плюс учесть токи, втекающие в узел, а со знаком минус – вытекающие из узла.

2. Выбрать независимые контуры, число которых равно:

(НК) = (В) – (Y- 1)

Независимые контуры - контуры, отличающиеся друг от друга хотя бы одной новой ветвью.

3. Выбрать положительные направления обхода контуров (произвольно). Составить (В) - (Y - 1) уравнений по второму закону Кирхгофа для независимых контуров (НК), следуя правилу: если направление тока в ветви и направление обхода контура совпадают, напряжение на участке записать со знаком плюс. В противном случае - со знаком минус. Аналогично выбирают знак ЭДС.

4. Объединить уравнения, составленные по первому и второму законам Кирхгофа в систему алгебраических уравнений. Подставить численные значения и решить систему уравнений.

Пример 1.

Дано: Е 1=50 В Е 2=400 В R 1=50 Ом R 2=20 Ом R 3=50 Ом R 4=80 Ом Определить токи в ветвях цепи (рис.1.4).

Рис. 1.4

 

 

Решение.

 

1. Произвольно зададим направления токов в ветвях цепи. В схеме 3 ветви (В = 3), два узла (Y = 2). По первому закону Кирхгофа можно составить одно независимое уравнение, (Y – 1) = (2 – 1) = 1:

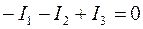
2. Число независимых контуров:

(В) – (Y – 1) = 3 – (2 – 1) = 2

3. Выбираем направление обхода контуров по часовой стрелке, составляем два уравнения по второму закону Кирхгофа:

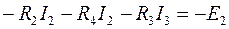
4. Составляем систему из уравнений, составленных по первому и второму законам Кирхгофа, подставляем численные значения:

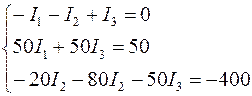
Решив систему уравнений, получим:

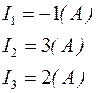
Метод контурных токов

Метод контурных токов основан на введении промежуточных неизвестных переменных - контурных токов. Контурный ток – условный ток каждого независимого контура. Уравнения составляются по второму закону Кирхгофа и поэтому их число равно количеству независимых контуров (НК) = (В) – (Y- 1). Токи ветвей определяют алгебраическим суммированием контурных токов.

Для того чтобы рассчитать электрическую цепь методом контурных токов необходимо:

1. Выбрать в расчетной схеме независимые контуры и проставить произвольно положительные направления контурных токов (например, по часовой стрелке) в схеме.

2. Для каждого независимого контура составить контурное уравнение на основании второго закона Кирхгофа и свести их в систему.

 

 

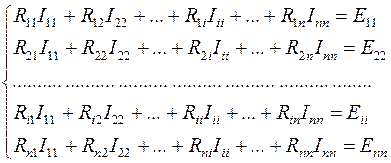
Где:

– контурный ток i –го контура;

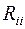– собственное сопротивление i -го контура, равное сумме сопротивлений ветвей, входящих в этот контур;

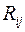– сопротивление ветви, входящей одновременно в i –ый контур и j –ый контур, взятое со знаком плюс, если направления контурных токов I_ii и I_jj в этой ветви совпадают;

E_ii – контурная ЭДС i -го контура, равная алгебраической сумме ЭДС, входящих в этот контур и взятых со знаком плюс, если направления этих ЭДС совпадают с направлением тока I_ii.

3. Объединив полученные контурные уравнения в систему линейных алгебраических уравнений, и подставив заданные значения параметров, решить систему и найти контурные токи.

4. Используя полученные контурные токи, определить токи ветвей для чего:

a. Выбрать произвольно положительные направления токов ветвей, показать их на схеме.

b. В ветвях, по которым проходит лишь один контурный ток, искомые токи ветвей равны соответствующим контурным токам.

c. В смежных между контурами ветвях искомые токи ветвей определить алгебраической суммой контурных токов, прилегающих к данной ветви контуров.

 

Пример 2.

 

 

Дано: Е 1=20 В Е 2=5 В Е 3=35 В R 1=10 Ом R 2=5 Ом R 3=5 Ом R 4=15 Ом R 5=5 Ом Определить токи в ветвях цепи (рис.1.5).

 

Рис. 1.5

 

Решение.

 

1. Зададим произвольно направления токов в ветвях, направления контурных токов выберем по часовой стрелке (рис.1.6):

 

 

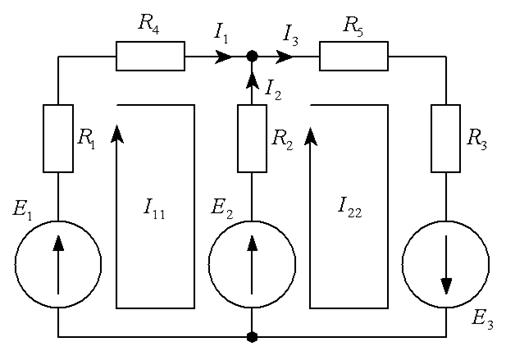
Рис. 1.6

2. Составим систему уравнений по методу контурных токов:

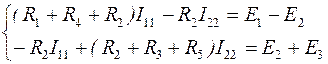
3. Подставим численные значения и, решив систему, найдем контурные токи:

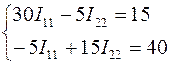
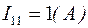
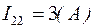
4. Определим токи в ветвях:

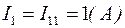
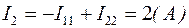
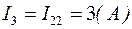
Метод узловых потенциалов

Метод узловых потенциалов основан на первом законе Кирхгофа. Потенциал одного из узлов цепи принимают равным нулю, поэтому число уравнений, составляемых по методу узловых потенциалов, равно (Y - 1), где (Y) – число узлов схемы.

Для того чтобы рассчитать электрическую цепь методом узловых потенциалов необходимо:

1. Обозначить в расчетной схеме все узлы, потенциал одного из узлов принять равным нулю, задать произвольно направления токов.

2. Составить систему уравнений по методу узловых потенциалов:

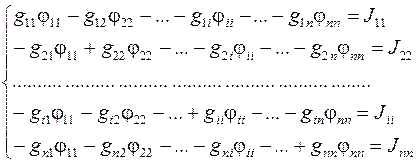
Где:

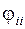- потенциал i –го узла:

- сумма проводимостей ветвей, сходящихся в узле i;

- сумма проводимостей ветвей, непосредственно соединяющих узел i и узел j;

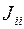- узловой ток i -го узла, равный сумме произведений проводимостей ветвей, сходящихся в узле i на ЭДС, действующие в этих ветвях. Причем ЭДС считается положительной, если направлена к узлу i, и отрицательной, если направлена от узла i.

3. Определить токи в ветвях цепи, используя обобщенный закон Ома (закон Ома для участка цепи, содержащего источник ЭДС).

Пример 3

Дано: Е 1=20 В Е 2=5 В Е 3=30 В R 1=10 Ом R 2=5 Ом R 3=10/3 Ом R 4=10 Ом R 5=5 Ом Определить токи в ветвях цепи используя метод узловых потенциалов (рис.1.7).

Рис. 1.7

 

Решение.

1. Обозначим в расчетной схеме все узлы, потенциал узла 3 примем равным нулю (φ₃₃= 0), зададим произвольно направления токов в ветвях (рис 1.8).

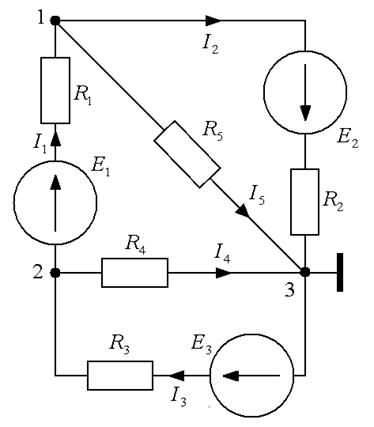
Рис.1.8

2. Составим систему уравнений по методу узловых потенциалов:

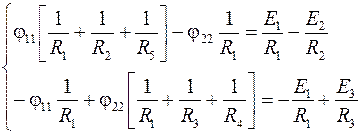
Подставим численные значения и решим систему:

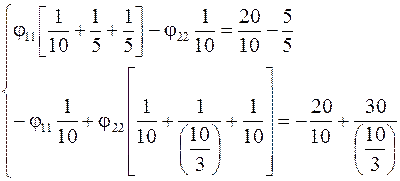
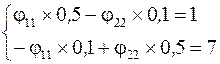
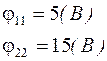
3. Определим токи в ветвях цепи, используя обобщенный закон Ома:

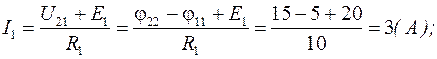
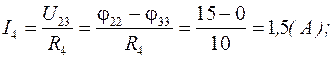
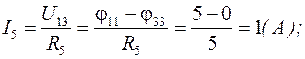
Метод эквивалентного генератора

Метод эквивалентного генератора основан на применении теоремы об эквивалентном источнике (генераторе) и служит для расчета тока в отдельной ветви разветвленной цепи. В любой электрической цепи можно выделить одну ветвь, а всю остальную часть цепи независимо от ее структуры и сложности можно рассматривать по отношению к удаленной ветви как двухполюсник - активный, если внутри двухполюсника имеется источник энергии, или пассивный, если источник энергии отсутствует.

Для расчета электрической цепи методом эквивалентного генератора необходимо:

1. Выделить в расчетной цепи ветвь, ток которой необходимо определить. Остальную часть цепи представить в виде двухполюсника.

2. Выбрать положительное направление тока ветви и изобразить его на схеме.

3. Отсоединив выделенную ветвь, определить направление на зажимах двухполюсника – напряжение холостого хода одним из известных методов расчета.

4. Определить эквивалентное (входное) сопротивление двухполюсника по отношению к зажимам выделенной ветви. При этом считать сопротивление идеальных источников ЭДС равным нулю. Предварительно изобразить схему двухполюсника без источников энергии.

5. Изобразить неразветвленную цепь, введя в нее ветвь, ток которой определяется и эквивалентный источник с найденными параметрами - ЭДС (согласовав ее направление с положительным направлением напряжения холостого хода) и эквивалентным сопротивлением.

6. Определить по закону Ома ток полученной неразветвленной цепи, это есть искомый ток ветви сложной цепи. Для цепи постоянного тока:

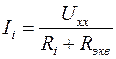
1.7.1 Пример 3.

Дано: Е 1=150 В Е 2=250 В R 1=10 Ом R 2=12 Ом R 3=40 Ом Определить ток в ветви, содержащей резистор R 2 (рис.1.9).

Рис. 1.9

Решение.

1. Выделим в расчетной цепи ветвь с резистором R ₂, ток которой необходимо определить. Остальную часть цепи представим в виде двухполюсника (рис.1.10).

 

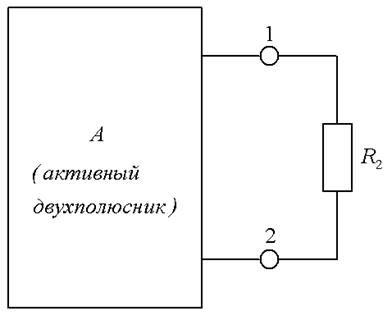
Рис. 1.10

 

2. Выберем положительное направление тока, который необходимо определить, и изобразим его на схеме (рис.1.11).

Рис. 1.11

3. Разорвем ветвь с сопротивлением R ₂ и определим напряжение холостого хода U_хх между точками разрыва 1 и 2 (рис.1.12). Для этого воспользуемся вторым законом Кирхгофа, учитывая, что в данном случае ток через сопротивления R ₁ и R ₃ одинаков, так как образовавшаяся цепь – простая:

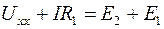
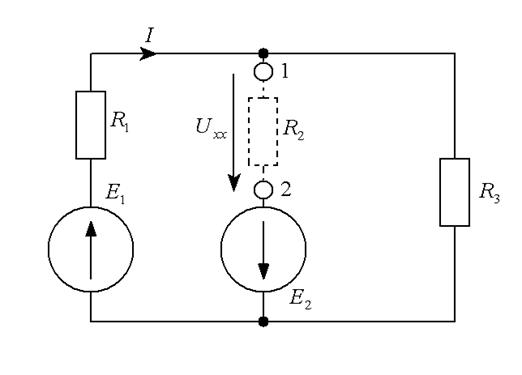
Рис. 1.12

 

 

Выразив U_хх, получим:

 

 

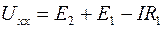
Определим ток I:

 

 

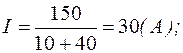
Напряжение холостого хода:

4. Определим эквивалентное (входное) сопротивление двухполюсника по отношению к зажимам выделенной ветви 1 и 2, предварительно изобразив схему двухполюсника без источников энергии (рис.1.13).

 

Рис. 1.13

 

Резисторы R ₁ и R ₃ по отношению к точкам разрыва 1 и 2 соединены параллельно, следовательно:

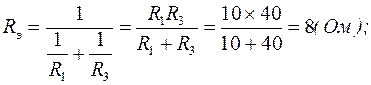
5. Изобразим неразветвленную цепь, введя в нее резистор R ₂, и эквивалентный источник с найденными параметрами - ЭДС и эквивалентным сопротивлением (рис.1.14).

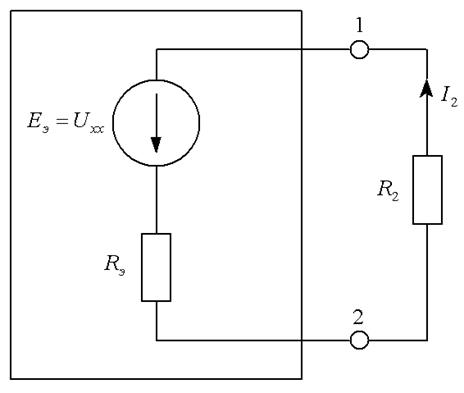
Рис. 1.14

6. Определим по закону Ома ток полученной неразветвленной цепи:

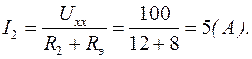
Потенциальная диаграмма

Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают последовательно сопротивления элементов контура, начиная с какой-либо произвольной точки, а по оси ординат - потенциалы точек контура относительно этой произвольной точки. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме. По потенциальной диаграмме можно определить разность потенциалов между любыми двумя точками контура.

Пример 4.

Построить потенциальную диаграмму для внешнего контура исходной схемы примера 2 (рис.1.15).

 

 

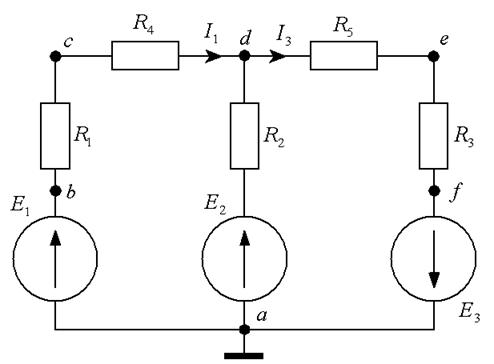
Рис.1.15

 

 

Решение.

Произвольно выбираем точку контура, потенциал которой считаем равным 0 (точка а). Обозначим на схеме точками участки цепи, входящие в контур, потенциал которых одинаков, но отличен от потенциала точки а. Укажем условные положительные направления токов контура, величины которых определены в задаче 2 (рис.1.15).

Найдем потенциалы выделенных точек контура по отношению к точке а и построим потенциальную диаграмму (рис.1.16).

 

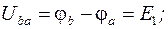следовательно:

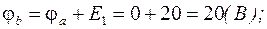
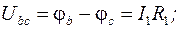следовательно:

следовательно:

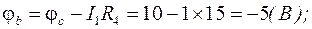
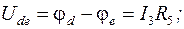следовательно:

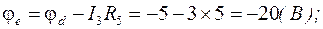
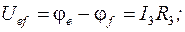следовательно:

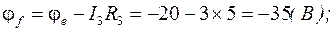
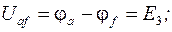следовательно:

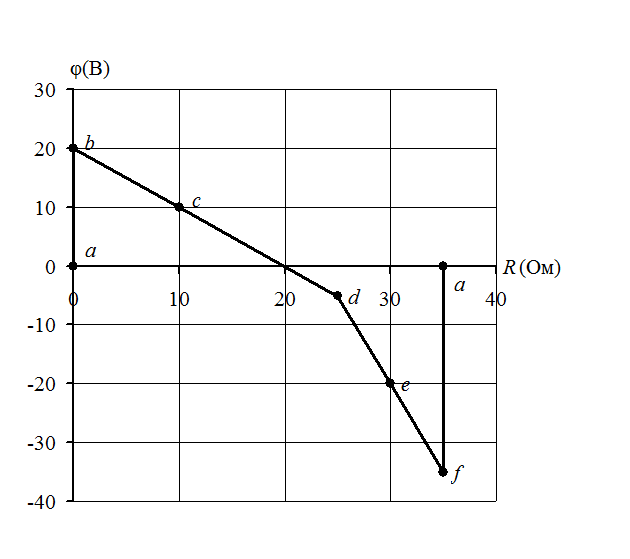
Рис. 1.16

Задание.

Для электрической схемы, соответствующей номеру варианта и изображенной на рис. 2.1 – 2.18, выполнить следующее:

2.1 Упростить схему, заменив последовательно и параллельно соединенные резисторы ветвей эквивалентными. Дальнейший расчет вести для упрощенной схемы.

2.2 Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

2.3 Определить токи во всех ветвях схемы методом контурных токов.

2.4 Определить ток в заданной по условию ветви (номер ветви указан в таблице 1), используя метод эквивалентного генератора.

2.5 Начертить потенциальную диаграмму для внешего контура.

 

Исходные данные для каждого варианта даны в таблице 1.

Указания: При выполнении пункта 2.4 для определения входного сопротивления двухполюсника следует преобразовывать схему соединения резисторов треугольником в эквивалентную схему соединения звездой или наоборот.

 

 

Таблица 1	№ ветви
E6	- - -	- - -	- - -	- - -	- - -	- - -	- - -	- - -	- - -
E5	- -	- -	- - -	-	- -	- - -	- - -	- -	-
E4	- - -	- -	-	- - -	- - -	- -	- -	- -	- - -
E3		12.5
E2			4.5
E1	-	- -	- -	- -	-	-	-	- -	-
R6’’			∞ 7.5
R6’				5.5
R5’’							3.5
R5’		10.5 11.5		5.5		5.5
R4’’				10.5			5.5	6.5
R4’			4.5 6.5					6.5 6.5	7.5
R3		4.5 5.5					6.5		11.5 8.5
R2	7.5			5.5	10.5 5.5	6.5		2.5	2.5
R1						4.5
рисунок	2.13 2.2 2.10	2.2 2.11 2.1	2.5 2.18 2.18	2.10 2.1 2.17	2.1 2.13 2.8	2.11 2.5 2.2	2.4 2.8 2.5	2.18 2.10 2.13	2.6 2.12 2.7
№ группы
№ по спис
Продолжение таблицы 1	№ ветви
E6	- -	- - -	- -	- - -	- - -	- - -	- -	- - -	- - -
E5	- - -	- - -	- -	- -	- - -	- - -	- - -	-	- - -
E4	- - -	- -	- - -	- -	- - -	- - -	- -	- - -	- -
E3
E2	-		-				-
E1	19.5	-	-	- -			-	- -	-
R6’’	16.5
R6’
R5’’	13.5
R5’					3.5
R4’’	5.5
R4’
R3	13.5 7.5
R2	7.5				5.5
R1	19.5				4.5
рисунок	2.15 2.6 2.3	2.3 2.6 2.4	2.12 2.15 2.9	2.7 2.3 2.11	2.16 2.6 2.11	2.2 2.14 2.3	2.16 2.3 2.15	2.7 2.2 2.7	2.17 2.11 2.13
№ группы
№ по спис
	Окончание таблицы 1	№ ветви
	E6	- - -	- - -	- - -	- - -	- - -	- - -	- - -
	E5	- - -	-	-	- -	- -	- - -	- - -
	E4	- - -	- - -	- - -	- - -	- -	- -	- - -
	E3
	E2
	E1		- -	- -	-	- -	-
	R6’’
	R6’
	R5’’
	R5’
	R4’’
	R4’
	R3
	R2
	R1
	рисунок	2.8 2.8 2.5	2.1 2.7 2.2	2.14 2.1 2.10	2.9 2.17 2.1	2.11 2.16 2.12	2.13 2.4 2.6	2.5 2.9 2.16
	№ группы
	№ по спис

 

Рис.2.1

Рис.2.2

Рис.2.3

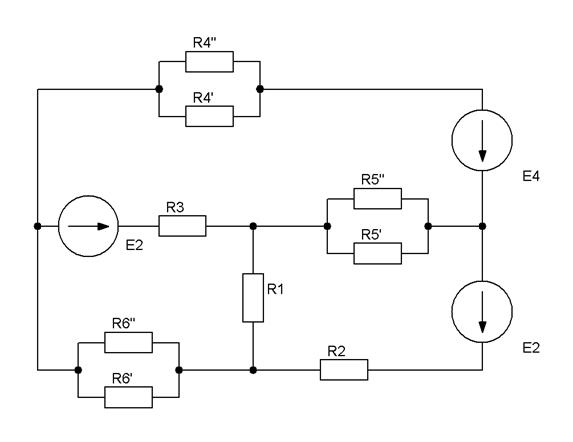
Рис.2.4

Рис.2.5

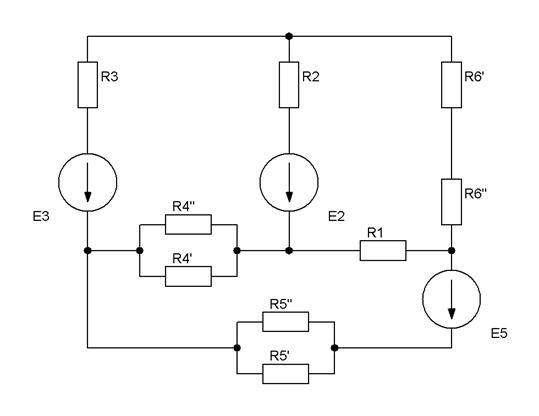
Рис.2.6

Рис.2.7

Рис.2.8

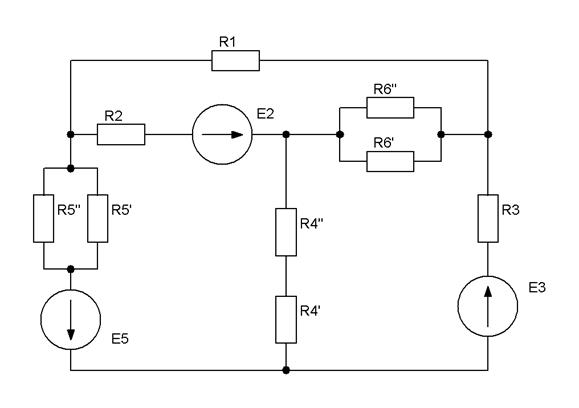
Рис.2.9

Рис.2.10

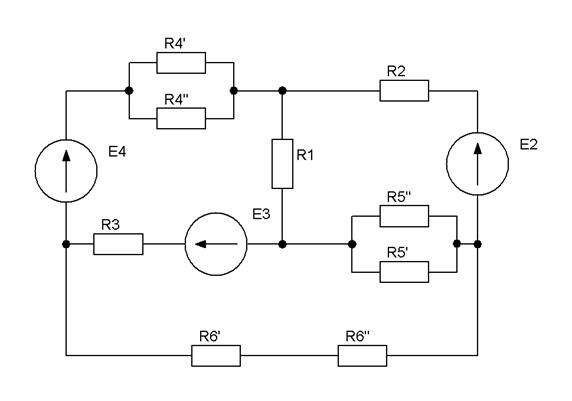
Рис.2.11

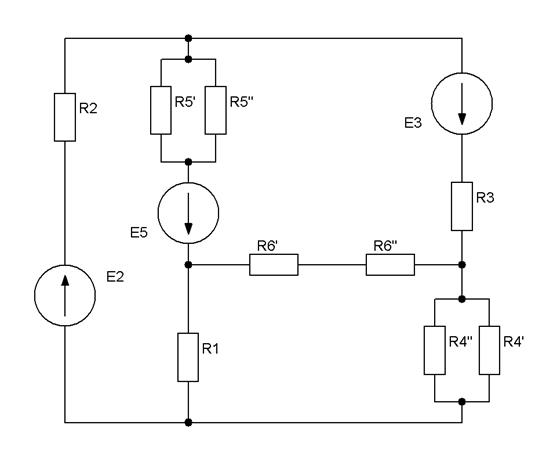
Рис.2.12

Рис.2.13

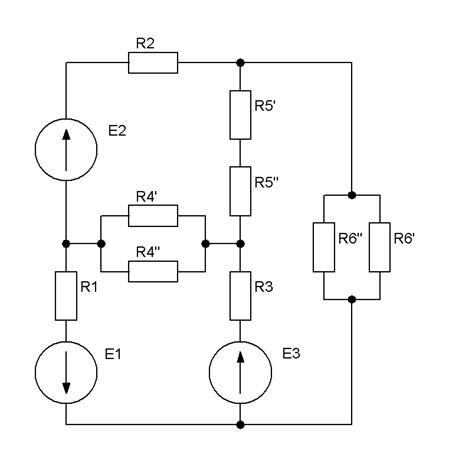
Рис.2.14

Рис.2.15

Рис.2.16

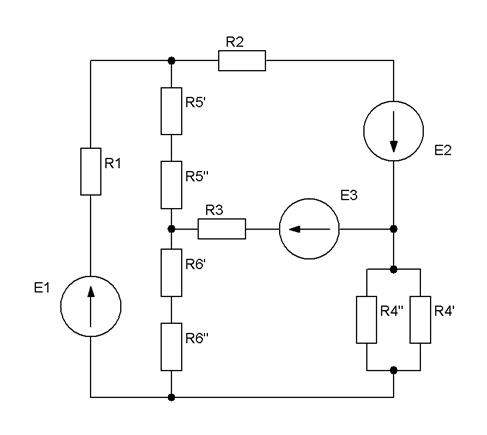
Рис.2.17

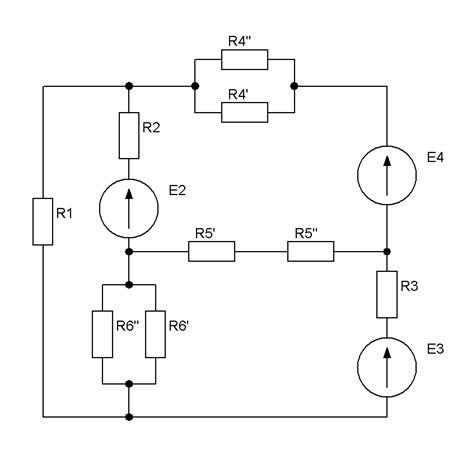
Рис.2.18

 

Библиографический список

1. Электротехника. Под ред. В.Г.Герасимова. – М.: Высшая школа, 1985.

2. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника.- М.: Энергоатомиздат. 1985.

3. Волынский Б.А., Зейн Е.Н., Шатерников В.Е.Электротехника.- М.: Энергоатомиздат. 1987.

Поделиться:

Воспользуйтесь поиском по сайту: