 |
Определение положения центра тяжести сложного сечения
|
|
|
|
СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Учебно-методическое пособие
для самостоятельной работы студентов
Барнаул 2004
УДК 539.3/.8
Сопротивление материалов: Учебно-методическое пособие для самостоятельной работы студентов / Сост.: Ю.Ф. Загороднев, Л.В. Якименко, Д.Н. Пирожков. Барнаул, 2004. – 85 с.
В учебно-методическом пособии даны краткие теоретические сведения по изучаемым разделам дисциплины, необходимые при выполнении студентами контрольных заданий. Рассмотрены примеры решения практических задач. Приведены задания для контрольных работ.
Предназначено студентам инженерных специальностей.
Рекомендовано к изданию методической комиссией ИТАИ (протокол № 4 от 1 июля 2003 г.).
Рецензент – доцент каф. механизации животноводства Сергеев В.Д.
© Алтайский государственный аграрный университет, 2004
ВВЕДЕНИЕ
Сопротивление материалов – это наука об инженерных методах расчетов элементов машин и конструкций на прочность, жесткость и устойчивость. В сопротивлении материалов широко применяются методы теоретической механики и математики, а также используются данные из разделов физики, в которых изучаются различные свойства материалов. Изучение дисциплины сопротивление материалов следует начать с основных понятий, таких как: расчетная схема и составляющие ее элементы: стержни, оболочки, пластины и массивные тела. При расчетах стержневых конструкций следует вспомнить сведения, изучаемые в курсе статики, а именно виды опор: шарнирные подвижные и неподвижные, глухая заделка, а также вспомнить какие реакции возникают в каждом виде этих опор. Необходимо усвоить, что сопротивление материалов решает три основных задачи: проверочный расчет, проектный расчет, определение грузоподъемности. При решении этих задач основным методом сопротивления материалов является метод сечений, когда проводится сечение тела некоторой поверхностью, и после ввода внутренних сил между разрезанными частями, рассматривается равновесие одной из частей. Необходимо запомнить, что в общем случае нагружения в поперечном сечении стержня может возникать шесть внутренних силовых факторов: нормальная сила, две поперечных силы, два изгибающих момента и крутящий момент. Следует обратить внимание на то, что конструкции могут быть как статически определимые (решаемые при помощи статики), так и статически неопределимые (решаемые при помощи уравнений совместности деформаций).
|
|
|
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Выполняя контрольную работу, необходимо соблюдать следующие требования:
1) контрольная работа выполняется в ученической тетради синими чернилами, четким почерком с полями в 4 см для возможных замечаний рецензента;
2) на обложке тетради указать фамилию, имя, отчество, шифр, наименование предмета, номер контрольной работы, почтовый адрес с индексом отделения связи;
3) данные из таблиц для выполнения контрольной работы нужно брать в соответствии с личным шифром студента и первыми пятью буквами русского алфавита, которые следует расположить под шифром. Например, Ваш шифр 12345, тогда
| шифр | |||||
| буквы | а | б | в | г | д |
К каждой задаче контрольной работы дается таблица с исходными данными. Вертикальные столбцы этой таблицы обозначены буквами, а крайний левый столбец обозначает номер строки. Из каждого вертикального столбца таблицы (обозначен буквой) необходимо взять только одно значение, стоящее в горизонтальной строке, номер которой соответствует цифре вашего шифра, стоящей над буквой.
4) перед решением каждой задачи надо выписать ее условия с числовыми данными, а также выполнить соответствующий чертеж с указанием всех необходимых размеров и величин;
|
|
|
5) решение должно сопровождаться краткими последовательными и грамотными пояснениями, с указанием размерности всех получаемых величин;
6) вычисления должны производится с точностью то трех значащих цифр;
7) каждую задачу необходимо решать с новой страницы;
8) по получении проверенной контрольной работы студент должен исправить в ней все ошибки, сохраняя предыдущие неверные записи.
ЗАДАЧА 1
Для схемы, показанной на рисунке (табл. 2) необходимо:
1) Вычертить ее в произвольном масштабе.
2) Для произвольного поперечного сечения стержня записать уравнения внутренних силовых факторов.
3) Построить эпюры внутренних силовых факторов.
Указания к задаче 1
Для исследования прочности любого тела необходимо знать величину внутренних сил, возникающих в данном теле под действием на него внешних сил. Для определения внутренних сил в сопротивлении материалов используют метод сечений. В общем случае произвольного нагружения стержня в его поперечных сечениях могут возникать шесть внутренних силовых факторов:
- усилие вдоль оси z – продольная сила N;
- усилия вдоль осей х и у — поперечные силы Qx и Qy соответственно;
- момент относительно продольной оси z — крутящий момент МzºТкр;
- моменты относительно осей х и у — изгибающие моменты Мх и My соответственно.
Так как существует шесть внутренних силовых факторов, то при решении пространственных задач необходимо составлять шесть уравнений равновесия:
 .
.
Для определения опасного сечения, то есть сечения, в котором внутренние силы имеют наибольшую по абсолютному значению величину, необходимо строить эпюры.
Эпюрой внутренней силы называется график, отображающий изменение внутренней силы по длине бруса, при переходе от одного поперечного сечения к другому.
- усилие вдоль оси z — продольная сила N;
- усилия вдоль осей х и у — поперечные силы Qx и Qy соответственно;
- момент относительно продольной оси z — крутящий момент МzºТкр;
- моменты относительно осей х и у — изгибающие моменты Мх и My соответственно.
Так как существует шесть внутренних силовых факторов, то при решении пространственных задач необходимо составлять шесть уравнений равновесия:
|
|
|
 .
.
Для определения опасного сечения, то есть сечения, в котором внутренние силы имеют наибольшую по абсолютному значению величину, необходимо строить эпюры.
Эпюрой внутренней силы называется график, отображающий изменение внутренней силы по длине бруса, при переходе от одного поперечного сечения к другому.
ПРИМЕР
Для стержня изображенного на рис. 1а определить внутренние силовые факторы в произвольном поперечном сечении и их построить эпюры. F1 = 100 Н, F2 = 300 Н, q = 75 Н/м, a = 0,3 м, b = 0,2 м, l = 2 м.


а) б)
Рисунок 1.
Решение.
Рассекаем брус на произвольном расстоянии z от его свободного конца. Отбрасываем правую часть. Располагаем оси координат в центре тяжести сечения. Действие правой части бруса на его левую часть заменяем внутренними силами: N, Qx, Qy, Mx, My, Ткр (рис. 1 б).
Уравновешиваем, то есть, записываем уравнения равновесия и определяем значения внутренних силовых факторов.
 ;
;
QX = - 100Н.
 ;
;
при z = 0 Qy = 0;
при z = l Qy = -150 Н.
 ;
;
N = - 300Н.
 ;
;
при z = 0 Mx = - 45 Н×м;
при z = l Mx = -195 Н×м.
 ;
;
при z = 0 My = 30 Н×м; при z = l My = - 170 Н×м.
 ; Ткр = 15 Н×м.
; Ткр = 15 Н×м.
Строим эпюры внутренних силовых факторов (рис 2). Опасное сечение в данном брусе будет находиться в заделке, так как в этом сечении значения всех В.С.Ф. имеют наибольшие величины.

Рисунок 2
ЗАДАЧА 1
Для схемы, показанной на рисунке (табл. 2) необходимо:
4) Вычертить ее в произвольном масштабе.
5) Для произвольного поперечного сечения стержня записать уравнения внутренних силовых факторов.
6) Построить эпюры внутренних силовых факторов.
Таблица 1
Исходные данные к задаче № 1
| № п/п | l, м | с, м | F1, кН | F2, кН | номер схемы |
| 1,1 | 0,2 | ||||
| 1,2 | 0,3 | ||||
| 1,3 | 0,4 | ||||
| 1,4 | 0,5 | ||||
| 1,5 | 0,6 | ||||
| 1,6 | 0,7 | ||||
| 1,7 | 0,8 | ||||
| 1,8 | 0,9 | ||||
| 1,9 | 0,4 | ||||
| 2,0 | 0,7 | ||||
| а | б | в | г | д | |
Таблица 2
Расчетные схемы к задаче №1
|
|
|

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Указания к задаче 2
Растяжением называется такой вид деформации, при котором в поперечном сечении бруса, возникает единственный внутренний силовой фактор – продольная сила.
Для правильного составления уравнений равновесия, при действии на стержень продольной силы, необходимо знать правило знаков, представленное на рис. 3.
Нормальные напряжения при растяжении-сжатии определяются по формуле:

Рисунок 3.
, 
где S – площадь поперечного сечения стержня.
Условие прочности выглядит следующим образом:
 .
.
Деформации при растяжении-сжатии (абсолютное удлинение) определяется по формуле:
 ,
,
где l – длина стержня;
Е – модуль упругости первого рода.
Условие жесткости определяется неравенством вида:
 .
.
ПРИМЕР
Для схемы, изображенной на рис. 4, построить эпюру нормальной силы и определить удлинение стержня, если F1 = 100 кН, F2 = 50 кН, q = 40 кН/м, а= = 1 м, b = 2 м, с = 1,5 м, Е = 2×105 МПа, S = 0,2 м2.
Решение
1) Разбиваем брус на участки АВ, ВС, CD
2) Определяем значение нормальной силы на каждом участке
CD


CB


при  ,
,
при 

Рисунок 4.
BА


3) Строим эпюру нормальной силы (рис. 4)
4) Определяем удлинение стержня




ЗАДАЧА 2
Для вертикального стержня, имеющего жесткую заделку на одном из концов, изображенного на рисунке (табл. 4) необходимо:
1) Вычертить схему в произвольном масштабе.
2) Определить значения нормальной силы на каждом участке стержня.
3) Построить эпюру нормальной силы.
4) Определить удлинение стержня.
Длины участков стержня и нагрузки, приложенные к нему, приведены в табл. 3, площадь поперечного сечения узкого участка S = 0,2 м2, широкого участка 2 S.
Таблица 3
Исходные данные к задаче № 2
| № п/п | а, м | q1=q3, кН/м | q2, кН/м | F1, кН | F2, кН | F3, кН | номер схемы |
| 0,8 | |||||||
| 1,2 | |||||||
| 1,4 | |||||||
| 1,6 | |||||||
| 1,8 | |||||||
| 0,8 | |||||||
| 1,2 | |||||||
| а | д | в | г | б | в | д |
Таблица 4
Расчетные схемы к задаче №2

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
.
Указания к задаче 3
Кручение – это такой вид деформации стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент.
Внешние моменты, воздействующие на вал, называются скручивающими.
|
|
|
Расчет вала на прочность начинается с построения эпюры крутящего момента и отыскания опасного сечения.
Касательные напряжения при кручении определяются по формуле:
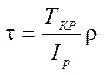 ,
,
где ТКР – крутящий момент, действующий в сечении;
r - радиус той точки поперечного сечения, в которой определяются напряжения;
Ip – полярный момент инерции сечения.
Условие прочности при кручении записывается следующим образом:
 .
.
где Wp – полярный момент сопротивления сечения.
Угол закручивания вала определяется по формуле:
 ,
,
где l – длина вала;
G – модуль упругости второго рода.
Условие жесткости при кручении записывается следующим образом:
 .
.
Полярный момент инерции и полярный момент сопротивления круглого сечения определяются по формулам соответственно:
 ,
,  ,
,
где d – диаметр вала.
Полярный момент инерции и полярный момент сопротивления кольцевого сечения определяются по формулам соответственно:
 ,
, 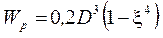 ,
,
где D – внешний диаметр вала;

d – внутренний диаметр вала.
ПРИМЕР
Для вала, изображенного на рис. 5, подобрать поперечное сечение круглой, кольцевой и прямоугольной форм, если Т1 =600 Нм, Т2 =1000 Нм, Т3 = =800Нм, Т4 = 1300 Нм, Т5 =1600Нм, x = 0,7, h/b = 2, [t] =100МПа. Построить эпюру углов закручивания для вала круглого поперечного сечения.

Рисунок 5.
Решение
1) Строим эпюру крутящего момента со свободного конца вала и определяем опасное сечение
АС

СД

ДЕ

ЕК

КВ 
Из эпюры крутящих моментов (рис. 9) видно, что опасным, является участок КВ, максимальное значение крутящего момента Ткр max = 1700 Нм.
2) Подбираем поперечное сечение вала
7.1) Круглое сечение
Условие прочности при кручении:
 где
где 

Принимаем d = 45 мм.
7.2) Кольцевое сечение


Принимаем D = 50 мм, тогда  мм.
мм.
7.3) Прямоугольное сечение

Для прямоугольного сечения с отношением h/b = 2 b = 0,493.

Тогда  м.
м.
3) Строим эпюру углов закручивания
Найдем момент инерции для круглого сечения:
 м4.
м4.





4) Сравним веса валов
Найдем площадь поперечного сечения для каждого из валов: круглого, кольцевого, прямоугольного.



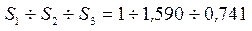
ЗАДАЧА 3
Для заданной расчетной схемы (табл.5) необходимо:
1) Вычертить расчетную схему вала в произвольном масштабе.
2) Построить эпюру крутящих моментов.
3) Из условия прочности определить размеры поперечного сечения вала, приняв сечение вала круглым, кольцевым, прямоугольным.
4) Построить эпюру углов закручивания для круглого вала, приняв жесткость сечения постоянной.
5) Сравнить веса валов.
Числовые данные взять из таблицы 5.
Таблица 5
Исходные данные к задаче № 3
| № п/п | М1, Н∙м | М2, Н∙м | М3, Н∙м | М4, Н∙м | М5, Н∙м | [t], МПа | а, м | b, м | с, м | 
| 
| № схе-мы |
| 0,2 | 0,7 | 0,5 | 0,4 | 1,1 | ||||||||
| 0,3 | 0,6 | 0,6 | 0,5 | 1,2 | ||||||||
| 0,4 | 0,5 | 0,4 | 0,6 | 1,3 | ||||||||
| 0,5 | 0,4 | 0,3 | 0,7 | 1,4 | ||||||||
| 0,6 | 0,3 | 0,5 | 0,8 | 1,5 | ||||||||
| 0,7 | 0,2 | 0,8 | 0,9 | 1,6 | ||||||||
| 0,8 | 0,3 | 0,7 | 0,8 | 1,7 | ||||||||
| 0,7 | 0,4 | 0,3 | 0,7 | 1,8 | ||||||||
| 0,6 | 0,5 | 0,4 | 0,6 | 1,9 | ||||||||
| 0,5 | 0,6 | 0,2 | 0,5 | 2,0 | ||||||||
| д | г | в | б | г | а | д | г | в | б | а | д |
Таблица 5
Расчетные схемы к задаче № 3

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Указания к задаче 4
Определение положения центра тяжести сложного сечения
Координаты центра тяжести любой сложной фигуры можно определить по формулам:
 ,
,  ,
,
где Sx, Sy – статические моменты площади сечений простых фигур, составляющих сложную фигуру;
S – площадь фигуры.
Сумма статических площадей простых фигур определяется по формуле:
 ,
,
 ,
,
где Si – площадь i-той простой фигуры;
xi, yi – координаты центра тяжести i -той простой фигуры.
ПРИМЕР 1
Определить положение центра тяжести фигуры, показанной на рис. 10.

Рисунок 6.
1) Выбираем произвольные оси координат
2) Разбиваем сечение на простейшие фигуры
3) Находим площадь каждой из фигур
 мм2;
мм2;
 мм2.
мм2.
4) Определяем статические моменты площади
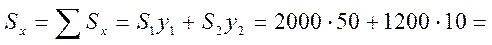
 мм3
мм3

 мм3
мм3
5) Находим координаты центра тяжести
 мм;
мм;  мм;
мм;
|
|
|


