Задание 1. Измерение зависимости ширины главного максимума дифракционной картины от ширины щели

Лабораторная работа №6

Соотношение неопределённостей для фотонов

Цель работы: экспериментальное подтверждение выполнения соотношения неопределённостей для фотонов.

Приборы и принадлежности: источник света - лазер, щель регулируемой ширины, оптическая скамья, экран, линейка, микроскоп.

Введение

Соотношение неопределенностей является одним из фундаментальных принципов современной физики. Для квантовых частиц можно сформулировать следующим образом. Неопределенность положения частицы ∆х и неопределенность проекции ее импульса на то же направление ∆р­_­х должны удовлетворять соотношению

(1)

В данной работе соотношение неопределенностей (1) проверяется экспериментально для фотонов. Проявлением принципа неопределенности в оптике может служить явление дифракции. Действительно, при ограничении поперечных размеров светового пучка щелью шириной ∆х неопределенность координаты фотонов, из которых состоит пучок, равна ширине этой щели. Тогда будет отличной от нуля и неопределенность проекции импульса фотонов вдоль направления, перпендикулярного щели, т.е. в диафрагмированном излучении будут присутствовать фотоны, которые движутся не только в прежнем направлении, но и под некоторым углом α к нему. Проекция импульса таких фотонов на направление, перпендикулярное направлению первоначального пучка, будет равна .Если при дифракции основная доля излучения будет сосредоточена в диапазоне углов от -α до α, то неопределенность импульса будет составлять .Следовательно, произведение неопределенностей координаты и импульса будет равно

где λ – длина волны излучения.

Из этого неравенства следует, что угловая расходимость светового пучка после дифракции на щели шириной ∆х определяется неравенством

Это с точностью до порядка соответствует классической теории дифракции, в которой эта величина равна

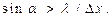
Здесь угол α определяет направления на первые минимумы дифракционной картины.

В работе предлагается измерить ширину щели, характеризующую неопределенность координаты фотона ∆х, и ширину дифракционной картины, характеризующую неопределенность поперечного импульса фотона ∆р_х .

Описание экспериментальной установки

Установка для проверки принципа неопределённостей (рис.1) состоит из источника монохроматического излучения (гелий-неоновый лазер) 1, оптической скамьи 2, на которой могут располагаться калиброванная щель 3 переменной ширины, экран со шкалой 4, калибровочный микроскоп 5.

Рис.1

Измерение и обработка результатов

Испускаемый гелий-неоновым лазером пучок света проходит через калиброванную щель и попадает на экран, где наблюдается исследуемая дифракционная картина. Меняя с помощью барабана ширину щели, можно наблюдать изменение вида дифракционной картины.

Задание 1. Измерение зависимости ширины главного максимума дифракционной картины от ширины щели

Установите щель и экран на оптической скамье согласно рис.1 на расстоянии, указанном в паспорте установки. Для этого, используя салазки, на которых установлена калиброванная щель, добейтесь того, чтобы луч лазера прошел через нее и попал на экран.

Меняя ширину щели, проведите не мене 5 измерений ширины 2D главного максимума дифракционной картины. Ширину щели меняйте с шагом в два деления по шкале барабана от значения, когда на экране уже отчетливо наблюдается дифракционная картина, до значения, при котором еще можно наблюдать изменение ширины главного максимума. Измерьте ширину главного максимума, пользуясь шкалой экрана. Для увеличения точности измерений установите калиброванную щель на расстоянии не менее 1м от экрана. Ширину максимума определите по положению темных полос, окаймляющих максимум.

Результаты измерения ∆х (в делениях шкалы барабана), 2D и D (в мм) (половина ширины главного максимума) занесите в табл.1.

Поделиться:

Воспользуйтесь поиском по сайту: