 |
Опасное состояние материала наступает тогда, когда на некоторой площадке осуществляется наиболее неблагоприятная комбинация нормального и касательного напряжений.
|
|
|
|
Вопросы к Задаче 1
1 Какой стержень называют стержнем большой жесткости?
Стержень большей жесткости – стержень, деформации которого бесконечно малы по сравнению с его размерами.
2 Какова структура формулы для определения нормальных напряжений в произвольной точке поперечного сечения при внецентренно приложенной продольной силе? Какой вид имеет эпюра напряжений?
Внецентренное растяжение (сжатие) представляет собой случай нагружения, при котором линия действия равнодействующей внешних сил параллельна оси стержня z, но не совпадает с ней. Пусть в торцевом сечении стержня в точке А с координатами (хF, уF) приложена равнодействующая внешних сил F.
В произвольном поперечном сечении стержня возникают три внутренних силовых фактора, постоянных по его длине:
Здесь хFуF – координаты точки приложения равнодействующей внешней нагрузки F (координаты полюса силы). Таким образом, внецентренное растяжение (сжатие) представляет собой сочетание косого изгиба с центральным растяжением или сжатием. Нормальное напряжение в произвольной точке поперечного сечения В (х, у) определяется следующим выражением:
или
Отношения 
и 
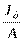представляют собой квадрат радиусов инерции сечения:
.
С учетом этих обозначений формула принимает вид
При определении напряжений по формуле величины хF, х, уF, у берутся с учетом их знака относительно координатных осей. В условиях внецентренного сжатия перед правой частью формулы ставится знак минус.
Эпюры напряжений:
3 Как определяется положение нейтральной линии при внецентрированном растяжении или сжатии?
При сложном профиле сечения стержня для определения опасной точки предварительно находится положение нейтральной линии. Учитывая, что на нейтральной линии напряжения равны нулю, тогда:
|
|
|
где х 0 и у 0 – координаты любой точки нейтральной линии. Уравнение нейтральной линии будет иметь вид:
Это – уравнение прямой, не проходящей через начало координат.
По уравнению можно определить отрезки, отсекаемые нейтральной линией на координатных осях. Обозначим эти отрезки через ах и ау.
Если принять, что у 0= 0, х 0 = ах, то из уравнения получим:
Принимая х 0 = 0, у 0 = ау, будем иметь:
Решая эти уравнения, получим отрезки, отсекаемые нейтральной линией на координатных осях:
, 
.
Исследование этих формул показывает, что точка приложения силы и нейтральная ось лежат по разные стороны относительно центра тяжести сечения.
Нейтральная линия делит поперечное сечение стержня на две зоны – сжатую и растянутую. Проводя параллельно нейтральной линии касательные к контуру сечения, найдем опасные точки С и D, лежащие в растянутой и сжатой зонах.
Условие прочности для стержня из пластичного материала запишется в виде
Где х оп и y оп – координаты точки, наиболее удаленной от нейтральной линии.
Для стержней, выполненных из неравнопрочного материала, расчет на прочность ведется для двух опасных точек (в растянутой и сжатой зонах).
Условия прочности имеют вид:
,
где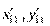 
и 
– координаты опасных точек соответственно в растянутой и сжатой зонах.
4 Может ли нейтральная линия находиться вне поперечного сечения?
Нулевая линия при косом изгибе не проходит перпендикулярно к силовой линии. Угол между нейтральной и силовой линиями будет прямым, только если главные центральные моменты инерции равны (
), но это не прямой изгиб.
Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).
5 В каком случае нейтральная линия перпендикулярна одной из главных осей инерции сечения?
|
|
|
Для нахождения главных осей симметричного сечения достаточно найти положение его центра тяжести. Одной из главных центральных осей является ось симметрии, вторая ось ей перпендикулярна. Если ось, перпендикулярная оси симметрии, проходит и не через центр тяжести сечения, т. е. ось симметрии и любая, ей перпендикулярная, образуют систему главных осей.
Следовательно нейтральная линия перпендикулярна одной из главных осей инерции сечения.
Вопросы к Задаче 2
6 Что называют напряженным состоянием в точке тела?
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по трем взаимно перпендикулярным площадкам (сечениям), содержащим данную точку.
7 Сколько компонентов напряжений необходимо знать для однозначного определения напряженного состояния в точке тела?
Исследуя напряженное состояние в данной точке деформируемого тела, в ее окрестности выделяют бесконечно малый (элементарный) параллелепипед, ребра которого направлены вдоль соответствующих координатных осей. При действии на тело внешних сил на каждой из граней элементарного параллелепипеда возникают напряжения, которые представляют нормальными и касательными напряжениями проекциями полных напряжений на координатные оси
Нормальные напряжения обозначают буквой σ с индексом, соответствующим нормали к площадке, на которой они действуют. Касательные напряжения обозначают буквой τ с двумя индексами: первый соответствует нормали к площадке, а второй - направлению самого напряжения (или наоборот).
Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов напряжения. Их можно записать в виде следующей квадратной матрицы:
Эта совокупность напряжений называется тензором напряжений.
Тензор напряжений полностью описывает напряженное состояние в точке, то есть если известен тензор напряжений в данной точке, то можно найти напряжения на любой из площадок, проходящих через данную точку.
Нормальное напряжение σ считается положительным, если совпадает по направлению с внешней нормалью 
к площадке, касательные напряжения τ считаются положительными, если вектор касательных напряжений следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью. Отрицательными считаются напряжения обратных направлений.
|
|
|
8 Какие площадки и напряжения называют главными?
Главные площадки - три взаимно перпендикулярные площадки в окрестности исследуемой точки, на которых касательные напряжения равны нулю.
9 Какие бывают виды напряженного состояния?
В зависимости от числа главных напряжений отличных от нуля напряженные состояния бывают:
1.1) Трехосные или объемные напряженные состояния – случай, когда ни одно из главных напряжений не равно нулю.
1.2) Напряженное состояние называется двухосным или плоским, если только два главных напряжения отличны от нуля. В этом случае кубический инвариант 
равен нулю. Характеристическое уравнение принимает вид
1.3) Если кубический 
и квадратичный инвариант одновременно равны нулю, то лишь одно главное напряжение отлично от нуля. Оно называется одноосным или линейным и возникает, например, при растяжении и сжатии при чистом изгибе.
10 Как нумеруют главные напряжения?
Главные напряжения принято обозначать буквой σ с цифрами 1, 2 и 3 в нижнем индексе.
При этом наибольшее с учетом знака напряжение обозначается как σ1 а наименьшее соответственно σ3.
Напряжение, расположенное на числовой оси правее других – σ1, а то, которое левее всех σ3.
11 Что понимают под так называемым упрощенным плоским напряженным состоянием? В каких случаях нагружения стержня оно возникает?
Упрощенное плоское напряженное состояние наиболее часто встречается при практических инженерных расчетах, так как именно этот тип напряженного состояния имеет место в точках бруса в общем случае его нагружения. Частным случаем плоского напряженного состояния является чистый сдвиг. При чистом сдвиге в окрестности точки можно выделить элемент, чтобы по четырем его граням действовали только равные по модулю касательные напряжения, а две грани были от напряжений свободны.
|
|
|
12 Что представляет собой круговая диаграмма О.Мора?
Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.
|
Рисунок 1 – Круговая диаграмма О.Мора.
s1 - максимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке;
s3 - минимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке;
tmax = 
- максимальное касательное напряжение, которое может возникнуть в точке на любой наклонной площадке, действует на площадках наклоненных к главным на угол 45°.
|
Вопросы к Задаче 3
13 Что называется эквивалентным напряжением?
Эквивалентное напряжение – напряжение, равное напряжению одноосного растяжения элемента материала, который равнопрочен тому же элементу при сложном напряженном состоянии.
14 Какие напряжения возникают в поперечных сечениях стержня при поперечном изгибе с кручением?
Изгиб с кручением стержня возникает тогда, когда внешние силы (включая и реакции внешних связей) создают на участках стержня моменты сил относительно продольной оси стержня (примем за продольную ось – ось х) и координатных осей y и z, лежащих в плоскости рассматриваемого поперечного сечения. Для круглого поперечного сечения стержня любые оси поперечного сечения, проходящие через его центр тяжести – главные центральные оси. Поэтому оси y и z являются главными центральными осями инерции поперечного сечения.
В опасном сечении вала при изгибе с кручением одновременно возникают наибольшие крутящий (
) и результирующий изгибающий 
момент.
15 Какие точки в поперечном сечении круглого стержня являются опасными при изгибе с кручением?
Для круглых стержней 
и косой изгиб для них невозможен, поэтому расчет можно вести на 
, определяемый по. Плоскость изгиба перпендикулярна и 
.
Наиболее опасными точками в круглом сечении являются точка а и точка b, где действуют 
и 
и возникает плоское напряженное состояние.
16 Как определяют эквивалентный момент в сечении по гипотезе максимальных касательных напряжений? По гипотезе октаэдрических касательных напряжений?
Напряженные состояния при сочетании основных деформаций и одноосном растяжении называют равноопасными или эквивалентными, если их главные напряжения отличаются от предельного для данного материала в одинаковое число раз, т. е. коэффициенты запаса прочности для эквивалентных напряжений одинаковы.
|
|
|
Ээквивалентным считается такое напряжение при простом одноосном растяжении, которое равноопасно данному сочетанию основных деформаций.
Таким образом, условие прочности при сочетании основных деформаций, когда в поперечных сечениях действуют и нормальные и касательные напряжения, будет иметь вид: σэкв ≤ [σp].
Формулы для определения эквивалентных напряжений, которые затем сопоставляют с предельно допускаемыми, выводят на основании гипотез прочности.
Гипотезы прочности – это научные предположения об основной причине достижения материалом предельного напряженного состояния при сочетании основных деформаций.
В настоящее время при вычислении эквивалентных напряжений используют три гипотезы прочности: гипотезу наибольших касательных напряжений (или третья гипотеза прочности), гипотезу Мора (четвертая гипотеза прочности) и энергетическую гипотезу (пятая гипотеза прочности).
Применявшиеся ранее при расчетах первая (гипотеза Галилея) и вторая (гипотеза Мариотта-Сен-Венана) гипотезы прочности, основанные соответственно на наибольших нормальных напряжениях и линейных деформациях, в настоящее время не используются, поскольку плохо подтверждаются опытами.
Чтобы вывести формулу для вычисления эквивалентных напряжений по третьей теории прочности, рассмотрим брус, у которого в поперечном сечении действуют нормальные σ и касательные τ напряжения.
Формула для вычисления эквивалентных напряжений:
Гипотеза наибольших касательных напряжений хорошо подтверждается опытами, в особенности для пластичных материалов.
17 Как записывают условие прочности при сложном напряженном состоянии в опасной точке в случае пластичного материала?
При сложном напряженном состоянии разрушение произойдет при условии, что 
безопасное состояние или условие прочности по этой теории запишется в виде:
Это условие может быть выполнено при:
Использование второй теории в случае сжатия, когда 
позволяет объяснить причины разрушения хрупких материалов по площадкам, параллельным направлению сжимающей силы, а также объяснить, почему сопротивление хрупких материалов сжатию значительно выше их сопротивления растяжению.
При растяжении:
а при сжатии:
Вопросы к Задаче 4
18 Что называют эквивалентным напряжением?
Эквивалентное напряжение – напряжение, равное напряжению одноосного растяжения элемента материала, который равнопрочен тому же элементу при сложном напряженном состоянии.
19 Как определяют эквивалентное напряжение по критериям пластичности? По теории Мора?
Гипотеза Мора, предложенная им в начале XX века может быть сформулирована так.
Опасное состояние материала наступает тогда, когда на некоторой площадке осуществляется наиболее неблагоприятная комбинация нормального и касательного напряжений.
По сути, это усовершенствованная и обобщенная гипотеза наибольших касательных напряжений, тем не менее, она дает возможность определять эквивалентные напряжения в балках с меньшей степенью погрешности и применима при расчетах на прочность как пластичных, так и хрупких материалов.
Формула для вычисления эквивалентных напряжений, согласно гипотезе Мора имеет вид:
Где 
;
√ - знак корня.
Очевидно, что при k = 1 формула Мора тождественна формуле третьей теории прочности (гипотезе наибольших касательных напряжений).
20 Какие точки являются опасными в стержне прямоугольного сечения при сочетании изгиба, растяжения и кручения?
Рассмотрим брус прямоугольного сечения, нагруженный таким образом, что в его поперечных сечениях действуют изгибающие моменты M z и M y, а также крутящий момент M x.
Чтобы проверить прочность бруса, нужно в опасном сечении найти опасную точку, вычислить для нее эквивалентное напряжение (по одной из теорий прочности) и сопоставить его с допускаемым напряжением.
Для нахождения опасной точки сечения построим эпюры напряжений от всех силовых факторов.
Эпюры нормальных и касательных напряжений показывают, что, в отличие от круглого сечения, точки, в которых максимальные нормальные и максимальные касательные напряжения, не совпадают. Вследствие этого, условие прочности составляют, как минимум для трех наиболее опасных точек поперечного сечения.
Опасной точкой по нормальным напряжениям является точка С, в которой 
от M y и от M z положительны, или точка A, в которой от M y и от M z также одного знака, но отрицательны. Касательные напряжения от крутящего момента в этих точках равны нулю. Таким образом, в этих точках имеет место линейное напряженное состояние.
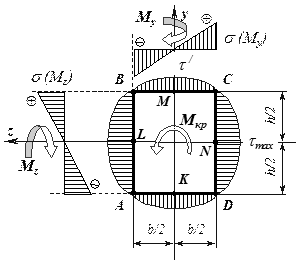
Опасной точкой по касательным напряжениям является точка N (или L), лежащая в середине длинной стороны прямоугольника. В этой точке действуют максимальные нормальные напряжения от изгибающего момента M y.
В точке M (или K), расположенной в середине короткой стороны также действуют касательные напряжения (несколько меньшие 
) и максимальные нормальные напряжения от M z.
Таким образом, в точках поперечного сечения N, M, (L, K) имеет место плоское напряженное состояние, которое обуславливает использование гипотез прочности при расчетах на прочность. Для пластичных материалов применяют III (наибольших касательных напряжений) и IV (энергетическую) гипотезы прочности.
Составим условия прочности для трех предположительно опасных точек поперечного сечения точке C:
Точке N:
Точке M:
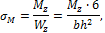
Расчетная формула по четвертой гипотезе прочности
Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к третьей гипотезе, а для очень хрупких – к первой гипотезе
21 Какие точки являются опасными в стержне круглого поперечного сечения при сочетании изгиба, растяжении и кручения?
У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента Mx, и My, а целесообразно их заменить результирующим (суммарным) изгибающим моментом:
,
который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору Мизг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру Мизг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.
Строится эпюра крутящего момента Мz.
Наибольшие напряжения изгиба возникают в точках k и k\, наиболее удаленных от нейтральной оси,
.
Где Wизг — момент сопротивления при изгибе.
В этих же точках имеют место и наибольшие касательные напряжения кручения
,
Где Wр — момент сопротивления при кручении.
22 Как записывают условие прочности в случае сложного напряженного состояния в опасной точке для пластичных материалов? Для хрупких материалов?
Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к третьей гипотезе, а для очень хрупких – к первой гипотезе
Вопросы к Задаче 5
23 Что понимают под потерей устойчивости сжатого стержня?
|
|
|
