Характеристики статистического распределения

В описательной статистике центральное место занимает оценивание параметров выборки.

Точечное оценивание параметров распределения

Точечная оценка - количественная характеристика генеральной совокупности, функция от наблюдаемых случайных величин. Далее речь пойдет о точечном оценивании параметров распределения.

Рассмотрим свойства точечных оценок.

А) Несмещенной оценкой параметра θ называется статистическая оценка θ*, математическое ожидание которой равно θ: М (θ*)= θ.

Если М (θ*) > θ (или М (θ*) < θ), то возникает систематическая ошибка (неслучайная ошибка, искажающая результаты измерений в одну сторону). Несмещенность оценки является гарантией защиты от систематических ошибок.

Б) Однако несмещенная оценка не всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения θ* могут быть сильно рассеяны вокруг своего среднего значения (дисперсия D (θ*) может быть велика). Тогда найденная по данной выборке оценка, например θ* ₁, может оказаться удаленной от М (θ*), а значит и от θ. Поэтому естественным вслед за несмещенностью, является требование малости дисперсии.

Эффективной называют оценку, которая при данном объеме выборки имеет наименьшую дисперсию.

В) При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности. Состоятельной называют оценку, которая при n→∞ по вероятности стремиться к оцениваемому параметру:

Например, если дисперсия несмещенной оценки стремиться к нулю при n→∞, то такая оценка оказывается и состоятельной.

Перейдем к оцениванию параметров распределения.

Параметры распределения – это его числовые характеристики. Они указывают, где в среднем располагаются значения признака (мера положения), насколько значения изменчивы (мера рассеяния), ихарактеризуют отклонение распределения от нормального (мера формы). В реальных условиях исследования мы оперируем не параметрами, а их приближенными значениями – оценками параметров, которые являются функциями от наблюдаемых величин. Заметим, что чем больше выборка, тем ближе может быть оценка параметра к его истинному значению.

Пусть x₁, x₂, … x_к вариационный ряд и n₁, n₂, … n_к - частоты соответствующих вариант, n – объем выборки.

Показатели положения

Выборочная средняя (оценка математического ожидания) – характеризует центр группирования данных (мера положения). Обозначается , вычисляется по формуле:

Если дано интервальное статистическое распределение, то выборочная средняя определяется для соответствующих интервалов .

Где - середина интервала .

Выборочная средняя является несмещенной и состоятельной оценкой.

Медиана - значение признака, приходящееся на середину упорядоченного по возрастанию вариационного ряда. Если ряд состоит их (2 N +1) вариант, то медианой является (N +1)-е значение варианта, если ряд состоит из 2 N вариант, то медиана равна полусумме N – го и (N +1) – ого значений вариант.

Мода - вариант с наибольшей частотой. Если таких вариант несколько (у них одна и та же частота), то распределение называют полимодальным.

Показатели вариации

Размах – разница между наибольшим и наименьшим значениями вариант.

(3)

Выборочная дисперсия (оценка дисперсии) – характеристика рассеяния наблюдаемых значений количественного признака выборки вокруг своего среднего значения. Обозначим D_в - выборочную дисперсию

Можно показать, что М(D_в) = (n/(n-1))D_в. Поэтому исправленная (несмещенная) дисперсия, которую будем обозначать через , равна

В случае интервального распределения заменяем на .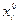

Кроме выборочной дисперсии для характеристики рассеяния пользуются сводной характеристикой - средним квадратическим отклонением (стандартом) σ

Коэффициент вариации служит для сравнения величины рассеяния по отношению к выборочной средней двух вариационных рядов. Рассеяние по отношению к выборочной средней больше для того ряда, для которого коэффициент вариации больше

5.1.3. Показатели формы распределения

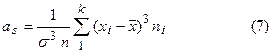Выборочная асимметрия – характеристика симметричности распределения. Обозначается . Для симметричных распределений (в том числе для нормального распределения) асимметрия равна нулю. Если , то «длинная часть» кривой распределения расположена справа от математического ожидания, если , то слева от математического ожидания (рис.2.).

Выборочный эксцесс – характеристика «подъема, крутости» кривой распределения. Обозначается . Для нормального распределения эксцесс равен нулю. При , то кривая имеет более высокую и острую вершину, если , то кривая имеет более низкую вершину, чем нормальная кривая (рис.1).

Рис.1 Рис.2

Замечание. Вышеуказанные характеристики статистических распределений можно вычислять с помощью EXCEL, используя возможности мастера функций или с помощью встроенного пакета «Анализ».

Итак, все указанные выше оценки являются точечными. Однако при небольших объемах выборок точечные оценки могут значительно отличаться от оцениваемого параметра. По этой причине при выборках небольшого объема следует использовать интервальные оценки.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: