 |
Электромагнитные колебания. Переменный ток.
|
|
|
|
ФИЗИКА
Задания для тестового контроля аудиторной и самостоятельной работы студентов на практических занятиях по курсу общей физики
Часть 2
Электричество и магнетизм
Учебно-методическое пособие
Ростов-на-Дону
Составители:
С.И. Егорова
В.С. Ковалева
В.С. Кунаков
Г.Ф. Лемешко
Ю.М. Наследников
УДК 530.1
Ф.48 Физика: Задания для тестового контроля аудиторной и самостоятельной работы студентов на практических занятиях по курсу общей физики. Часть 2. Электричество и магнетизм: Учебно-методическое пособие. – Ростов н/Д: Издательский центр ДГТУ, 2005 - с.
Цель пособия – обеспечить личностно-ориентированный подход к практическим занятиям по общей физике, учитывающий степень подготовки студентов и количество аудиторных часов, выделяемых на лекционные и практические занятия по курсу общей физики. Пособие предназначено для обучения и контроля работы студентов на практических занятиях по разделу «Электричество и магнетизм» в течение второго семестра обучения.
Печатается по решению редакционно-издательского совета Донского государственного технического университета
Научный редактор: д.т.н. проф. В.С. Кунаков
Рецензент: д.т.н. проф. Ю.М. Вернигоров
© Издательский центр ДГТУ, 2005
Общие методические указания
Структура практических занятий по курсу физики реализуется в трех семестров обучения, каждый из которых разбит на три блока рейтингового контроля знаний. С целью обеспечения дифференцированного подхода и объективности контроля аудиторной и самостоятельной работы студентов на практических занятиях по электричеству и магнетизму подобраны задачи в рамках тестовых заданий.
|
|
|
Они содержат задачи с выбором ответа и задачи с развернутым ответом, отмеченные звездочкой.
При оформлении задач с развернутым ответом необходимо соблюдать следующие требования:
1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины, приведенные в справочных таблицах «Приложения».
2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график, выполненные с помощью чертежных принадлежностей.
3. Решать задачу надо в общем виде, выразив искомую величину в буквенных обозначениях, заданных в условии задачи.
4. Произвести вычисления.
При оформлении заданий с выбором ответа необходимо привести номер задачи с указанием подраздела курса (напр., 1.25) и выбранный ответ в буквенном или числовом виде. Необходимо дать краткое без пояснений решение задачи, что позволяет выяснить ход рассуждений студента, степень ошибки или правильного ответа.
В «Приложении» даются варианты контрольных заданий.
В течение семестра студенты выполняют две контрольные работы: первую по электростатике и вторую по магнетизму.
В случае неудовлетворительной оценки по контрольной работе студент самостоятельно исправляет ошибки и сдает контрольную работу на повторную проверку. Результаты тестового контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и зачетов.
Электростатика
Основные формулы и законы
· Закон Кулона
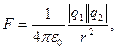
где F – модуль силы взаимодействия двух точечных зарядов q 1 и q 2в вакууме; r – расстояние между зарядами; e0 – электрическая постоянная, равная 8,85×10-12 Ф/м.
· Напряженность и потенциал электростатического поля
|
|
|
 ;
;  , или
, или  ,
,
где  - сила, действующая на точечный положительный заряд
- сила, действующая на точечный положительный заряд 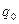 , помещенный в данную точку поля;
, помещенный в данную точку поля;  - потенциальная энергия заряда
- потенциальная энергия заряда 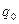 ;
;  - работа по перемещению заряда
- работа по перемещению заряда 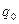 из данной точки поля за его пределы.
из данной точки поля за его пределы.
· Напряженность и потенциал электростатического поля точечного заряда  на расстоянии
на расстоянии  от заряда
от заряда
 ;
;  .
.
· Поток вектора напряженности через площадку 
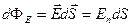 ,
,
где  - вектор, модуль которого равен
- вектор, модуль которого равен  , а направление совпадает с нормалью
, а направление совпадает с нормалью  к площадке;
к площадке; 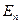 - составляющая вектора
- составляющая вектора  по направлению нормали
по направлению нормали  к площадке.
к площадке.
· Поток вектора напряженности через произвольную поверхность 
 .
.
· Принцип суперпозиции (наложения) электростатических полей
 ;
;  ,
,
где  ,
,  - соответственно напряженность и потенциал поля, создаваемого зарядом
- соответственно напряженность и потенциал поля, создаваемого зарядом  .
.
· Связь между напряженностью и потенциалом электростатического поля
 , или
, или 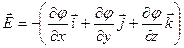 ,
,
где  ,
,  ,
,  - единичные векторы координатных осей.
- единичные векторы координатных осей.
· В случае поля, обладающего центральной или осевой симметрией
 .
.
· Электрический момент диполя (дипольный момент)
 ,
,
где  - плечо диполя.
- плечо диполя.
· Линейная, поверхностная и объемная плотность зарядов, т.е. заряд, приходящийся соответственно на единицу длины, поверхности и объема:
 ;
;  ;
;  .
.
· Теорема Гаусса для электростатического поля в вакууме
 ,
,
где  - алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; N – число зарядов; r - объемная плотность зарядов.
- алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; N – число зарядов; r - объемная плотность зарядов.
· Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью,
 .
.
· Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R с общим зарядом q на расстоянии r от центра сферы,
E = 0 при r < R (внутри сферы);
 при r ³ R (вне сферы).
при r ³ R (вне сферы).
· Напряженность поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью радиусом R на расстоянии r от оси цилиндра,
E = 0 при r < R (внутри цилиндра);
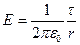 при r ³ R (вне цилиндра).
при r ³ R (вне цилиндра).
· Работа, совершаемая силами электростатического поля при перемещении заряда q 0 из точки 1 в точку 2,
 , или
, или  ,
,
где  - проекция вектора
- проекция вектора  на направление элементарного перемещения
на направление элементарного перемещения  .
.
· Поляризованность диэлектрика
 ,
,
где V – объем диэлектрика;  - дипольный момент i- й молекулы.
- дипольный момент i- й молекулы.
· Связь между поляризованностью и напряженностью электростатического поля внутри диэлектрика
 æ e 0
æ e 0  ,
,
|
|
|
где æ – диэлектрическая восприимчивость вещества.
· Связь диэлектрической проницаемости e с диэлектрической восприимчивостью æ
e = 1 + æ.
· Связь между напряженностью E поля в диэлектрике и напряженностью E 0 внешнего поля
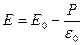 , или
, или  .
.
· Связь между векторами электрического смещения и напряженностью электростатического поля
 .
.
· Связь между  ,
,  и
и 
 .
.
· Теорема Гаусса для электростатического поля в диэлектрике
 ,
,
где  - алгебраическая сумма заключенных внутри замкнутой поверхности
- алгебраическая сумма заключенных внутри замкнутой поверхности  свободных электрических зарядов;
свободных электрических зарядов;  - составляющая вектора
- составляющая вектора  по направлению нормали
по направлению нормали  к площадке
к площадке  ;
;  - вектор, модуль которого равен
- вектор, модуль которого равен  , а направление совпадает с нормалью
, а направление совпадает с нормалью  к площадке. Интегрирование ведется по всей поверхности.
к площадке. Интегрирование ведется по всей поверхности.
· Электроемкость уединенного проводника и конденсатора
 ,
, 
 ,
,
где  - заряд, сообщенный проводнику;
- заряд, сообщенный проводнику;  - потенциал проводника; U – разность потенциалов между пластинами.
- потенциал проводника; U – разность потенциалов между пластинами.
· Электроемкость плоского конденсатора
 ,
,
где  - площадь пластины конденсатора;
- площадь пластины конденсатора;  - расстояние между пластинами.
- расстояние между пластинами.
· Электроемкость цилиндрического конденсатора
 ,
,
где 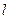 - длина обкладок конденсатора;
- длина обкладок конденсатора;  и
и 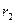 - радиусы внутренней и внешней обкладок конденсатора.
- радиусы внутренней и внешней обкладок конденсатора.
· Электроемкость сферического конденсатора
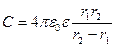 ,
,
где  и
и 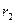 - радиусы концентрических сфер.
- радиусы концентрических сфер.
· Электроемкость системы конденсаторов соответственно при последовательном и параллельном соединениях
 и
и  ,
,
где  - электроемкость
- электроемкость  - го конденсатора;
- го конденсатора; 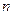 - число конденсаторов.
- число конденсаторов.
· Энергия уединенного заряженного проводника
 .
.
· Потенциальная энергия системы точечных зарядов
 ,
,
где ji – потенциал, создаваемый в той точке, где находится заряд qi, всеми зарядами, кроме i -го.
· Энергия заряженного конденсатора
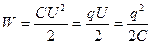 ,
,
где q – заряд конденсатора; C – его емкость; U - разность потенциалов между обкладками.
· Сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора
 .
.
· Энергия электростатического поля плоского конденсатора
 ,
,
где S – площадь одной пластины; U – разность потенциалов между пластинами; V=Sd – объем области между пластинами конденсатора.
· Объемная плотность энергии электростатического поля
 ,
,
|
|
|
где D – электрическое смещение.
1.1. Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусами 0,1 мм уравновешивается кулоновской силой отталкивания. Определите заряд капель. Плотность воды равна 1 г/см3.
А. [0,361 аКл] В. [3,61 аКл] С. [0,361 Кл] D. [361 Кл]
1.2. Два одинаковых заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Диэлектрическая проницаемость керосина e = 2.
А. [1,6 г/см3] В. [2,6 г/см3] С. [3,6 г/см3] D. [4,6 г/см3]
1.3. В вершинах равностороннего треугольника находятся одинаковые положительные заряды q = 2 нКл. Какой отрицательный заряд q 1 необходимо поместить в центр треугольника, чтобы сила притяжения со стороны заряда q 1 уравновесила силы отталкивания положительных зарядов?
А. [1,15 нКл] В. [1,15 Кл] С. [2,3 нКл] D. [2 нКл]
1.4. Свинцовый шарик (r1 = 11,3 г/см3) диаметром 0,5 см помещен в глицерин (r2 = 1,26 г/см3). Определите заряд шарика, если в однородном электростатическом поле шарик оказался взвешенным в глицерине. Электростатическое поле направлено вертикально вверх, и его напряженность 4 кВ/см.
А. [16,1 нКл] В. [11,3 нКл] С. [1,26 нКл] D. [4 Кл]
1.5. Определите напряженность электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды q 1 = 10 нКл и q 2 = -8 нКл и находящейся на расстоянии 8 см от отрицательного заряда. Расстояние между зарядами 20 см.
А. [10,1 кВ/м] В. [8 кВ/м] С. [101 В/м] D. [0,8 кВ/м]
1.6. Два точечных заряда 4 нКл и -2 нКл находятся друг от друга на расстоянии 60 см. Определите напряженность поля в точке, расположенной посередине между зарядами. Чему равна напряженность, если второй заряд положительный?
А. [0,6 кВ/м; 0,2 кВ/м] В. [0,6 В/м; 0,2 В/м]
С. [0,6 В/м; 0,2 кВ/м] D. [0,6 кВ/м; 0,2 В/м]
1.7. Расстояние l между двумя точечными зарядами ql = 2 нКл и q 2 = -3 нКл, расположенными в вакууме, равно 20 см. Определить: 1) напряженность Е; 2) потенциал j поля, создаваемого этими зарядами в точке, удаленной от первого заряда на расстояние r 1= 15 см и от второго заряда на r 2 = 10 см.
А. [ Е = 3кВ/м; 2) j = -150В] В. [ Е = 3В/м; 2) j = -150В]
С. [ Е = 3кВ/м; 2) j = -15 кВ] D. [ Е = 2кВ/м; 2) j = -3В]
1.8. Расстояние l между зарядами q = 2 нКл равно 20 см. Определите напряженность поля, созданного этими зарядами в точке, находящейся на расстоянии r 1 =15 см от первого и r 2 = 10 см от второго заряда.
А. [2,14 кВ/м] В. [2,14 В/м] С. [20 кВ/м] D. [15 кВ/м]
1.9. В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды q = 2 нКл. Определите напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата.
|
|
|
А. [1) 0; 2) 1,03 кВ/м] В. [1) 2 В/м; 2) 10,3 В/м]
С. [1) 2,5 В/м; 2) 1,03 кВ/м] D. [1) 0; 2) 1,03 В/м]
1.10. Определите поток ФЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды q 1 = 5 нКл и q 2 = -2 нКл.
А. [339 В×м] В. [3,39 В×м] С. [33,9 В×м] D. [10 В×м]
1.11. На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью 0,1 нКл/см2 расположена круглая пластинка. Нормаль к плоскости пластинки составляет с линиями напряженности угол 30°. Определите поток ФЕ вектора напряженности через эту пластинку, если ее радиус равен 15 см.
А. [3,46 кВ×м] В. [3,46 В×м] С. [0,1 кВ×м] D. [346 кВ×м]
1.12. Под действием электростатического поля равномерно заряженной бесконечной плоскости точечный заряд q = 1 нКл переместился вдоль силовой линии на расстояние 1 см; при этом совершена работа 5 мкДж. Определите поверхностную плотность заряда на плоскости.
А. [8,85 мкКл/м2] В. [8,85 мКл/м2]
С. [8,85 нКл/м2] D. [8,85 Кл/м2]
1.13. Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно одноименными зарядами с поверхностной плотностью соответственно s1 = 2нКл/м2 и s2 = 4 нКл/м2. Определите модуль напряженности электростатического поля: 1) между плоскостями; 2) за пределами плоскостей. Постройте график изменения напряженности поля вдоль линии, перпендикулярной плоскостям.
А. [1) 0,113 В/м; 2) 0,339 В/м] В. [1) 113 В/м; 2) 226В/м]
С. [1) 8 В/м; 2) 24 В/м] D. [1) 8 В/м; 2) 16 В/м]
1.14. Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно разноименными зарядами с поверхностной плотностью s1 = 1 нКл/м2 и s2 = - 2 нКл/м2. Определите модуль напряженности электростатического поля: 1) между плоскостями; 2) за пределами плоскостей.
А. [1) 0,169 В/м; 2) 0,0565 В/м] В. [1) 169 В/м; 2) 338 В/м]
С. [1) 169 мкВ/м; 2) 56,5 мкВ/м] D. [1) 169 мВ/м; 2) 338 мВ/м]
1.15. Электростатическое поле создается бесконечно длинной цилиндрической поверхностью радиусом 7 мм, равномерно заряженным с линейной плотностью t = 15 нКл/м. Определить: 1) напряженность Е поля в точках, лежащих от оси цилиндра на расстояниях r 1 = 5 мм и r 2 = 1 см; 2) разность потенциалов между двумя точками этого поля, лежащими на расстояниях r 3 = 1 см и r 4 = 2 см от поверхности цилиндра.
А. [1) E r1=0; E r2=27 кВ/м; 2) j3-j4 = 125 В]
В. [1) E r1=27 кВ/м; E r2=27 кВ/м; 2) j3-j4 = 125 кВ]
С. [1) E r1=27 В/м; E r2=27 В/м; 2) j3-j4 = 125 В]
D. [1) E r1=0; E r2=27 В/м; 2) j3-j4 = 125 кВ]
1.16. На металлической сфере радиусом 15 см находится заряд q = 2 нКл. Определите напряженность электростатического поля: 1) на расстоянии r 1= 10 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии r 2= 20 см от центра сферы.
А. [1) 0; 2) 800 В/м; 3) 450 В/м]
В. [1) 800 В/м; 2) 8 В/м; 3) 450 кВ/м]
С. [1) 800 В/м; 2) 800 кВ/м; 3) 450 В/м]
D. [1) 800 В/м; 2) 8 кВ/м; 3) 450 кВ/м]
1.17. Непроводящий шар радиусом 10 см в вакууме заряжен равномерно с объемной плотностью заряда 10 нКл/м3. Определите напряженность электростатического поля: 1) на расстоянии r 1 = 5 см от центра шара; 2) на расстоянии r2 = 15 см от центра шара.
А. [1) 18,8 В/м; 2) 16,7 В/м] В. [1) 18,8 кВ/м; 2) 16,7 кВ/м]
С. [1) 18,8 мВ/м; 2) 16,7 мВ/м] D. [1) 1 В/м; 2) 1 В/м]
1.18. Электростатическое поле создается положительно заряженной с постоянной поверхностной плотностью -10 нКл/м2 бесконечной плоскостью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния r 1= 2 см до r 2 = 1 см?
А. [9,04 • 10-19 Дж] В. [9,04 • 10-19 кДж]
С. [9,04 • 10-19 мкДж] D. [9,04 • 10-19 нДж]
1.19. Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью заряда 1 нКл/см. Какую скорость приобретет электрон, приблизившись к нити вдоль линии напряженности с расстояния r 1= 1,5 см до r 2 = 1 см от нити?
А. [16 Мм/с] В. [16 мм/с] С. [16 мкм/с] D. [16 м/с]
1.20. Одинаковые заряды q = 100 нКл расположены в вершинах квадрата со стороной 10 см. Определите потенциальную энергию этой системы.
А. [4,87 мДж] В. [4,87 мкДж] С. [4,87 нДж] D. [4,87 Дж]
1.21. Тонкое кольцо радиусом 5 см из тонкой проволоки имеет равномерно распределенный заряд q = 10 нКл. Определите потенциал j электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца.
А. [1) 1,8 кВ; 2) 805 В] В. [1) 1,8 В; 2) 805 кВ]
С. [1) 1,8 В; 2) 805 В] D. [1) 1,8 кВ; 2) 805 кВ]
1.22. Металлический шар радиусом 5 см имеет заряд q = 10 нКл. Определите потенциал электростатического поля: 1) на поверхности шара; 2) на расстоянии 2 см от его поверхности.
А. [1) 1,8 кВ; 2) 1,29 кВ] В. [1) 1,8 В; 2) 1,29 В]
С. [1) 1,8 кВ; 2) 1,29 В] D. [1) 1,8 В; 2) 1,29 кВ]
1.23. Сферическая поверхность имеет равномерно распределенный заряд. Определите радиус поверхности сферы, если потенциал в центре шара равен j1 = 200 В, а в точке, лежащей от его центра на расстоянии 50 см, j2 = 40 В.
А. [10 см] В. [10 м] С. [10 мм] D. [50 см]
1.24. Определите линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда q = 1 нКл с расстояния r 1 = 5 см до r 2 = 2 см равна 50 мкДж.
А. [3,03 мКл/м] В. [3,03 Кл/м]
С. [3,03 мкКл/м] D. [3,03 Кл/м]
1.25. Электростатическое поле создается положительно заряженной бесконечной нитью. Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния r 1= 1 см до r 2 = 5 см, изменил свою скорость от 1 до 10 Мм/с. Определите линейную плотность заряда нити.
А. [17,8 мкКл/м] В. [17,8 Кл/м]
С. [17,8 мКл/м] D. [17,8 нКл/м]
1.26. Определить ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, чтобы его скорость возросла от u 1 = 1 Мм/с до u2 = 5 Мм/с.
А. [68,3 В] В. [68,3 кВ] С. [68,3 мкВ] D. [68,3 мВ]
1.27. Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью s = 1 нКл/м2. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях х 1= 20 см и х 2 = 50 см от плоскости.
А. [16,9 В] В. [16,9 кВ] С. [16,9 мкВ] D. [16,9 мВ]
1.28. Определите поверхностную плотность зарядов на пластинах плоского слюдяного (e = 7) конденсатора, заряженного до разности потенциалов 200 В, если расстояние между его пластинами равно 0,5 мм.
А. [24,8 мкКл/м2] В. [24,8 Кл/м2]
С. [24,8 мКл/м2] D. [24,8 нКл/м2]
1.29. Электростатическое поле создается равномерно заряженной сферической поверхностью радиусом 10 см с зарядом q = 15нКл. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях 5 см и 15 см от поверхности сферы.
А. [360 В] В. [360 кВ] С. [360 мВ] D. [360 мкВ]
1.30. Электростатическое поле создается сферой радиусом 5 см, равномерно заряженной с поверхностной плотностью 1 нКл/м2. Определите разность потенциалов между двумя точками поля, расположенными на расстояниях 10 см и 15 см от центра сферы.
А. [0,94 В] В. [0,94 кВ] С. [0,94 мВ] D. [0,94 мкВ]
1.31. Электростатическое поле создается равномерно заряженным шаром радиусом 1 м и зарядом 50 нКл. Определите разность потенциалов для точек, расположенных от центра шара на расстояниях: 1) r 1 = 1,5 м, r 2 = 2 м; 2) r '1 = 0,3 м, r '2 = 0,8 м.
А. [1) 75 В; 2) 124 В] В. [1) 75 кВ; 2) 124 В]
С. [1) 75 В; 2) 124 кВ] D. [1) 75 кВ; 2) 124 кВ]
1.32. Электростатическое поле создается шаром радиусом 8 см, равномерно заряженным с объемной плотностью 10 нКл/м3. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях 10 см и 15 см от центра шара.
А. [0,64 В] В. [0,64 кВ] С. [0,64 мВ] D. [0,64 мкВ]
1.33. Электростатическое поле создается в вакууме непроводящим шаром радиусом 10 см, равномерно заряженным с объемной плотностью 20 нКл/м3. Определите разность потенциалов между точками, расположенными внутри шара на расстояниях 2 см и 8 см от его центра.
А. [2,26 В] В. [2,26 кВ] С. [2,26 мВ] D. [2,26 мкВ]
1.34. Электростатическое поле создается в вакууме бесконечным цилиндром радиусом 8 мм, равномерно заряженным с линейной плотностью 10 нКл/м. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях 2 мм и 7 мм от поверхности этого цилиндра.
А. [73 В] В. [73 кВ] С. [73 мВ] D. [73 мкВ]
1.35. Расстояние между пластинами плоского конденсатора 5 мм. После зарядки конденсатора до разности потенциалов 500 В между пластинами конденсатора поместили стеклянную пластинку (e = 7). Определите: 1) диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластинке.
А. [1) 6; 2) 759 нКл/м2] В. [1) 7; 2) 759 нКл/м2]
С. [1) 6; 2) 759 Кл/м2] D. [1) 7; 2) 759 Кл/м2]
1.36. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика — слюдяной пластиной (e 1 = 7) толщиной d 1 = 1 мм и парафиновой пластиной (e 2 = 2) толщиной d2 = 0,5 мм. Определите: 1) напряженности электростатических полей в слоях диэлектрика; 2) электрическое смещение, если разность потенциалов между пластинами конденсатора U = 500 В.
А. [1) Е 1= 182 кВ/м, Е2 = 637 кВ/м; 2) D = 11,3 мкКл/м2] В. [1) Е 1= 182 В/м, Е2 = 637 В/м; 2) D = 11,3 Кл/м2]
С. [1) Е 1= 14 В/м, Е2 = 32 В/м; 2) D = 1 Кл/м2] D. [1) Е 1= 14 кВ/м, Е2 = 32 кВ/м; 2) D = 1 мкКл/м2]
1.37. Расстояние между пластинами плоского конденсатора d = 5 мм, разность потенциалов U = 1,2 кВ. Определите: 1) поверхностную плотность заряда на пластинах конденсатора; 2) поверхностную плотность связанных зарядов на диэлектрике, если известно, что диэлектрическая восприимчивость диэлектрика, заполняющего пространство между пластинами, æ = 1.
А. [1) 4,24 мкКл/м2; 2) 2,12 мкКл/м2]
В. [1) 4,24 Кл/м2; 2) 2,12 мКл/м2]
С. [1) 4,24 мкКл/м2; 2) 2,12 мКл/м2]
D. [1) 4,24 Кл/м2; 2) 2,12 Кл/м2]
1.38. Пространство между пластинами плоского конденсатора заполнено стеклом (e = 7). Расстояние между пластинами d = 5 мм, разность потенциалов U = 1 кВ. Определите: 1) напряженность поля в стекле; 2) поверхностную плотность заряда на пластинах конденсатора; 3) поверхностную плотность связанных зарядов на стекле.
А. [1) 200 кВ/м; 2) 12,4 мкКл/м2; 3) 10,6 мкКл/м2]
В. [1) 200 В/м; 2) 12,4 мКл/м2; 3) 10,6 мКл/м2]
С. [1) 200 кВ/м; 2) 12,4 Кл/м2; 3) 10,6 Кл/м2]
D. [1) 200 В/м; 2) 12,4 Кл/м2; 3) 10,6 Кл/м2]
1.39. Определите расстояние между пластинами плоского конденсатора, если между ними приложена разность потенциалов U = 150 В, причем площадь пластин S = 100 см2, ее заряд q = 10 нКл. Диэлектриком является слюда (e = 7).
А. [9,29 мм] В. [9,29 м] С. [150 мм] D. [100 мм]
1.40. К пластинам плоского воздушного конденсатора приложена разность потенциалов U 1 = 500 В. Площадь пластин S = 200 см2, расстояние между ними d = 1,5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли парафин (e = 2). Определите разность потенциалов U2 между пластинами после внесения диэлектрика. Определите также электроемкости конденсатора C 1 и С2 до и после внесения диэлектрика.
А. [ U2 = 250 В, С 1 = 118 пФ, С 2 = 236 пФ]
В. [ U2 = 250 кВ, С 1 = 118 кФ, С 2 = 236 кФ]
С. [ U2 = 250 В, С 1 = 118 Ф, С 2 = 236 Ф]
D. [ U2 = 20 В, С 1 = 40 Ф, С 2 = 60 Ф]
1.41. Электроемкость батареи, образованной двумя последовательно соединенными конденсаторами, равна 100 пФ, а заряд батареи 20 нКл. Определите электроемкость второго конденсатора, а также разности потенциалов на обкладках каждого конденсатора, если электроемкость первого конденсатора200 пФ.
А. [ С 2 = 200 пФ; Dj1 = 100 В, Dj2 = 100 В]
В. [ С 2 = 200 Ф; Dj1 = 100 В, Dj2 = 100 В]
С. [ С 2 = 200 пФ; Dj1 = 100 пВ, Dj2 = 100 пВ]
D. [ С 2 = 200 Ф; Dj1 = 100 пВ, Dj2 = 100 пВ]
1.42. Шар, погруженный в масло (e = 2,2), имеет поверхностную плотность заряда s = 1 мкКл/м2 и потенциал j = 500 В. Определите: 1) радиус шара; 2) заряд шара; 3) электрическую емкость шара; 4) энергию шара.
А. [1) 9,74 мм; 2) 1,19 нКл; 3) 2,38 пФ; 4) 0,3 мкДж]
В. [1) 9,74 м; 2) 1,19 Кл; 3) 2,38 Ф; 4) 0,3 Дж]
С. [1) 9,74 мм; 2) 1,19 Кл; 3) 2,38 Ф; 4) 0,3 Дж]
D. [1) 9,74 мм; 2) 1,19 нКл; 3) 2,38 Ф; 4) 0,3 Дж]
1.43. Плоский воздушный конденсатор электроемкостью С = 10 пФ заряжен до разности потенциалов U 1= 500 В. После отключения конденсатора от источника тока расстояние между пластинами конденсатора было увеличено в 3 раза. Определите: 1) разность потенциалов на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин.
А. [1) 1,5 кВ; 2) 2,5 мкДж] В. [1) 1,5 В; 2) 2,5 Дж]
С. [1) 1,5 кВ; 2) 2,5 Дж] D. [1) 1,5 В; 2) 2,5 мкДж]
1.44. К пластинам плоского воздушного конденсатора приложено напряжение U 1= 500 В. Площадь пластин S = 200 см2, расстояние между ними d l = 1,5 мм. Пластины раздвинули до расстояния d2 = 15 мм. Найдите энергии W 1 и W2 конденсатора до и после раздвижения пластин, если источник тока перед раздвижением: 1) отключался; 2) не отключался.
А. [1) W 1= 14,8 мкДж, W 2 = 148 мкДж; 2) W 1= 14,8 мкДж; W 2 = 1,48 мкДж]
В. [1) W 1= 14,8 Дж, W 2 = 148 мДж; 2) W 1= 14,8 мДж; W 2 = 1,48 мДж]
С. [1) W 1= 14,8 Дж, W 2 = 148 Дж; 2) W 1= 14,8 Дж; W 2 = 1,48 Дж]
D. [1) W 1= 14,8 мДж, W 2 = 148 мДж; 2) W 1= 14,8 мкДж; W 2 = 1,48 мкДж]
1.45. Разность потенциалов между пластинами плоского конденсатора U = 100 В. Площадь каждой пластины S = 200 см2, расстояние между пластинами d = 0,5 мм, пространство между ними заполнено парафином (e = 2). Определите силу притяжения пластин друг к другу.
А. [7,08 мН] В. [7,08 Н] С. [7,08 нН] D. [7,08 мкН]
1.46. * Кольцо радиусом 5 см из тонкой проволоки равномерно заряжено с линейной плотностью t = 14 нКл/м. Определите напряженность поля на оси, проходящей через центр кольца, в точке А, удаленной на расстояние 10 см от центра кольца. [2,83 кВ/м]
1.47. * Поле создано двумя равномерно заряженными концентрическими сферами радиусами R 1= 5 см и R2 = 8 см. Заряды сфер соответственно равны q 1 = 2 нКл и q2 = -1 нКл. Определите напряженность электростатического поля в точках, лежащих от центра сфер на расстояниях: 1) r 1 = 3 см; 2) r 2 = 6 см; 3) r 3 = 10 см. [1) 0; 2) 5 кВ/м; 3) 0,9 кВ/м]
1.48. *Внутренний цилиндрический проводник длинного прямолинейного коаксиального провода радиусом R 1 = 1,5 мм заряжен с линейной плотностью t1 = 0,20 нКл/м. Внешний цилиндрический проводник этого провода радиусом R2 = 3 мм заряжен с линейной плотностью t2 = -0,15 нКл/м. Пространство между проводниками заполнено резиной (e = 3). Определите напряженность электростатического поля в точках, лежащих от оси провода на расстояниях: 1) r 1 = 1 мм; 2) r2 = 2 мм; 3) r 3 = 5 мм. [1) 0; 2) 800 В/м; 3) 180 В/м]
1.49.* На кольце с внутренним радиусом 80 см и внешним 1м равномерно распределен заряд 10 нКл. Определите потенциал в центре кольца. [100 В]
 2. Постоянный электрический ток
2. Постоянный электрический ток
Основные формулы и законы
 Сила тока
Сила тока

 ( если
( если  ).
).
 Плотность тока
Плотность тока
 ,
,
где S - площадь поперечного сечения проводника.
 Плотность тока в проводнике
Плотность тока в проводнике
 ,
,
где  -скорость упорядоченного движения зарядов в проводнике, n - концентрация зарядов, e - элементарный заряд.
-скорость упорядоченного движения зарядов в проводнике, n - концентрация зарядов, e - элементарный заряд.
 Зависимость сопротивления от параметров проводника
Зависимость сопротивления от параметров проводника
 ,
,
где l - длина проводника, S - площадь поперечного сечения проводника,  - удельное сопротивление,
- удельное сопротивление,  - удельная проводимость.
- удельная проводимость.
 Зависимость удельного сопротивления от температуры
Зависимость удельного сопротивления от температуры
 ,
,
где  - температурный коэффициент сопротивления,
- температурный коэффициент сопротивления,  - удельное сопротивление при
- удельное сопротивление при 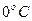 .
.
 Сопротивление при последовательном (а) и параллельном (б) соединении проводников
Сопротивление при последовательном (а) и параллельном (б) соединении проводников
а)  , б)
, б)  ,
,
где  - сопротивление
- сопротивление  го проводника, n – число проводников.
го проводника, n – число проводников.
 Закон Ома:
Закон Ома:
для однородного участка цепи
 ,
,
для неоднородного участка цепи
 ,
,
для замкнутой цепи
 ,
,
где U - напряжение на однородном участке цепи,  - разность потенциалов на концах участка цепи,
- разность потенциалов на концах участка цепи,  - ЭДС источника, r - внутреннее сопротивление источника тока.
- ЭДС источника, r - внутреннее сопротивление источника тока.
 Сила тока короткого замыкания
Сила тока короткого замыкания
 .
.
 Работа тока за время t
Работа тока за время t
 .
.
 Мощность тока
Мощность тока
 .
.
 Закон Джоуля-Ленца (количество теплоты, выделяемой при прохождении тока через проводник)
Закон Джоуля-Ленца (количество теплоты, выделяемой при прохождении тока через проводник)
 .
.
 Мощность источника тока
Мощность источника тока

 Коэффициент полезного действия источника тока
Коэффициент полезного действия источника тока
 .
.
 Правила Кирхгофа
Правила Кирхгофа
1)  - для узлов;
- для узлов;
2)  - для контуров,
- для контуров,
где 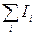 - алгебраическая сумма сил токов, сходящихся в узле,
- алгебраическая сумма сил токов, сходящихся в узле,  - алгебраическая сумма ЭДС в контуре.
- алгебраическая сумма ЭДС в контуре.
2.1. На концах медного провода длиной 5 м поддерживается напряжение 1 В. Определить плотность тока в проводе (удельное сопротивление меди


