 |
Двоично-десятичный счётчик
|
|
|
|
Двоично-десятичный счетчик является разновидностью недвоичного счетчика с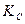 
=10. Счетчики строятся на основе четырехтриггерных двоичных счетчиков исключением шести избыточных состояний. Счетчики работают в различных двоично-десятичных кодах, часть из которых приведена в приложении 2. Особую группу составляют самодополняющие коды, характерной особенностью которых является соответствие обратных двоичных чисел обратным десятичным числам.
Порядок синтеза синхронных двоично-десятичных счетчиков принципиально не отличается от порядка синтеза недвоичных счетчиков. Разница заключается в том, что выбор комбинации шести исключаемых состояний определяется исходя из двоично-десятичного кода, в котором должен работать счётчик. В качестве примера рассмотрим синтез счетчика в простейшем коде 8-4-2-1. Таблица функционирования счетчика будет иметь вид табл. 7. Используя таблицу состояний счетчика, находим функции переходов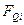 
. Для каждого разряда, карты которых даны на рис. 20.
Таблица 7
| № | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| ▲ | ||||||||||||
| ▲ | ▼ | |||||||||||
| ▲ | ||||||||||||
| ▲ | ▼ | ▼ | ||||||||||
| ▲ | ||||||||||||
| ▲ | ▼ | |||||||||||
| ▲ | ||||||||||||
| ▲ | ▼ | ▼ | ▼ | |||||||||
| ▲ | ||||||||||||
| ▼ | ▼ |
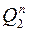
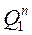
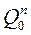
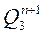
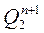
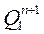
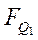
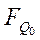
С помощью словаря переходов JK-триггера (см. табл. 2) получаем карты Карно для функций входов J и K триггеров в каждом разряде (рис. 21).
|
|
|
Рис. 20
После минимизации выражений функции входов J и K будут иметь вид:
, 
, 
, 
,
, 
, 
, 
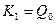Рис. 21
Счетчик реализуем на JK-триггерах, выполняющих операцию, "И" на входах. Схема счетчика показана на рис. 22.
Рис. 22
Моделирование счетчиков
Алгоритм моделирования счетчиков приведен на рис. 23, Вначале определяется тип кода. Если код равномерный, то заносятся начальный и конечный коды. Для того, чтобы определить, в каком режиме будет работать счетчик, производится сравнение начального и конечного кодов. Если начальный код меньше конечного, то выбирается режим суммирования и наоборот. Далее программным путем восстанавливается полная таблица переходов.
Если же код неравномерный, то осуществляется ввод последовательности кодов и строится таблица переходов.
На основании таблицы переходов определяется переключательная функция для каждого разряда счетчика 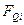, а затем (с помощью словаря переходов) - функции входов J и K для каждого разряда счетчика. Далее таблицы для J и K для каждого разряда счетчика минимизируются.
Квайном и Мак-Класки предложен следующий алгоритм минимизации логических функций /5/:
1. Составить таблицу для всех единичных точек (F=1) и неопределенных точек F=х функции 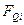, разбитых на классы 
,
, 
,... 
, где 
содержит все комбинации с i входными переменными. равными 1, и n-i переменными, равными 0.
Например, для четырехразрядного счетчика строятся классы ,
, , 
:
- содержит комбинацию, состоящую из нулей (т.е. 
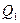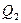=0, 
=0, 
=0, 
=0);
- комбинации из одной единицы и трех нулей (0001, 0010, 0100, 1000);
- комбинации из двух единиц и двух нулей (0011, 1001, 0110, 1100, 0101, 1010);
- комбинации из трех единиц и одного нуля (0111, 1011, 1101, 1110);
- комбинацию из четырех единиц 1111.
2. Сравнить каждый элемент в с каждым элементом +1 для всех i, 
.
|
|
|
Для пар, отличающихся только на один литерал X (отличие только в одном j разряде), образовать новые импликанты, покрывающие обе точки.
Эти импликанты не определены для 
, а оставшиеся переменные сохраняют те же значения, что и в паре комбинируемых строк. Новые импликанты поместить в класс , а строки, использованные для их образования, пометить знаком V.
Присвоить каждой новой строке 
=1, если хотя бы одна из строк, использованных, для её образования, имеет =1. Если обе строки имеют неопределенные метки, то это же значение присвоить новой строке.
3. Повторить шаг 2, используя ' и +1' для образования ''. Аналогично образовать ''' из " и Si+1" и продолжать эту процедуру до тех пор, пока дальнейшие комбинации окажутся невозможными. При этом неопределенные метки комбинируемых строк сохраняют неопределенность и во вновь образованных строках.
Строки, не учитываемые в процедуре (определяемые по отсутствию знака "V") являются простыми импликантами при условии, что они содержат метку , равную 1.
Таким образом, по окончании минимизации на экране дисплеи высвечиваются функции входов J и K для каждого разряда счетчика.
Приложение 1
Распространённые коды двоичных чисел
| Двоичное счисление | Обратный код | Дополнительный код | Циклический код Грея | |||||||||||||
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
|
|
|
Приложение 2
Распространённые двоично-десятичные коды чисел
| Десятичное число | Двоичный код
| Десятичные эквиваленты двоичных чисел в различных кодах | ||||||||
| Несамодополняющийся | Самодополняющийся | |||||||||
| 8-4-2-1 | 2-4-2-1 (код Айкена) | 4-2-2-1 | 5-2-1-1 | 5-4-2-1 | Невзвешенный | 2-4-2-1 | С избытком 3 | 4-2-2-1 | ||
| - | ||||||||||
| - | ||||||||||
| - | - | |||||||||
| - | ||||||||||
| - | - | - | - | |||||||
| - | - | - | - | |||||||
| - | - | - | ||||||||
| - | - | - | ||||||||
| - | - | - | - | - | ||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | - | - | - | ||||||
| - | - | - | - | |||||||
| - | - | - |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Алексеенко А.Г. Основы микросхемотехники. Элементы морфологии микроэлектронной аппаратуры. М.: Сов. Радио, 1971.
Алексеенко А.Г., Шагурин И.И. Микросхемотехника: учебное
пособие для вузов/ Под ред. И.П.Степаненко. М.: Радио и связь,
1982.
Букреев И.Н. и др. Микроэлектронные схемы цифровых устройств. Изд. 2-е, перераб. и доп. М.: Сов. Радио, 1975.
Проектирование радиоэлектронных устройств на интегральных микросхемах. Под ред. С.Я. Шаца. М.: Сов. Радио, 1976.
Фридман А., Шеннон П. Теория и проектирование переключательных схем. М.; Мир, 1978.
Составители Ю.В.ПАНОВ,
Т.C.ЛЕГОТКИНА
Корректор И.Н.ЖЕГАНИНА Формат 60х84/16. Объем 2 п.л. Тираж 100. Заказ 64. Бесплатно.
Редакционно-издательский отдел и ротапринт Пермского политехнического института
|
|
|
|
|
|
