Основные теоретические положения.

Лабораторная работа

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ

СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ И ПОЛУПРОВОДНИКОВ

ОТ ТЕМПЕРАТУРЫ И ОПРЕДЕЛЕНИЕ ЭНЕРГИИ

АКТИВАЦИИ ПОЛУПРОВОДНИКОВ.

 

СЕВЕРОДВИНСК

ЛАБОРАТОРНАЯ РАБОТА № 6

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ

ПРОВОДНИКОВ И ПОЛУПРОВОДНИКОВ

ОТ ТЕМПЕРАТУРЫ И ОПРЕДЕЛЕНИЕ

ЭНЕРГИИ АКТИВАЦИИ ПОЛУПРОВОДНИКОВ.

 

ЦЕЛЬ РАБОТЫ

Исследовать зависимость R=f(T) для проводника и lnR=f(1/T) для полупроводника. Вычислить температурный коэффициент сопротивления для проводника и энергию активации Δ E для полупроводника.

МЕТОД ИЗМЕРЕНИЯ– метод моста Уитстона.

 

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ.

В зависимости от величины электропроводности все вещества можно разделить на три группы: проводники, полупроводники и диэлектрики. Полупроводники характеризуются значениями электропроводности , промежуточными между электропроводностью металлов ) и хороших диэлектриков (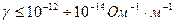). Электропроводность указана при комнатной температуре.

К проводникам относятся металлы, электролиты и плазма. Атомы металла легко отдают внешние (валентные) электроны. В кристаллической решетке металла не все электроны связаны со своими атомами. Некоторая их часть (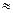 1 на атом) подвижна (свободна). Концентрация свободных электронов в металлах , чем и объясняется их хорошая проводимость и низкое удельное сопротивление.

По классической электронной теории проводимости металлов свободные электроны, находясь в состоянии хаотического теплового движения, образуют так называемый электронный газ, заполняющий пространство между узлами (положительными ионами) кристаллической решетки. Средняя скорость хаотического теплового движения и от температуры практически не зависит. Двигаясь со скоростью 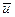электроны непрерывно сталкиваются с узлами решетки (и друг с другом), в

результате чего, направление движения электронов непрерывно меняется, следовательно, результирующая скорость теплового движения электронов в каком-то выделенном направлении равна нулю. Если же внутри проводника создать электрическое поле напряженностью E, то все свободные электроны начнут участвовать в направленном движении против поля, приобретая скорость упорядоченного движения, так как будут испытывать действие силы F=eE и получать ускорение ,

где e и m - заряд и масса электрона.

Предположим, что при соударениях с узлами кристаллической решетки электроны полностью теряют скорость v упорядоченного движения. Если - среднее время пробега электронов от соударения до соударения, то скорость электронов к концу пробега будет , а средняя скорость упорядоченного движения электронов равна:

.

Так как , где средняя длина свободного пробега электронов, то

(1)

Итак, под действием внешнего электрического поля в проводнике возникает упорядоченное движение электронов вдоль поля со средней скоростью , т.е. возникает электрический ток. Плотность тока j равна произведению величины заряда электрона e на число электронов , проходящих через единицу площади поперечного сечения проводника в единицу времени, т.е.

(2)

С учетом выражения (1) получим из (2) закон Ома в дифференциальной форме

(3)

 

где - называется удельной электропроводностью, а обратная ей величина - удельным сопротивлением.

(4)

По классической теории электропроводности скорость теплового движения электронов пропорциональна величине , т.е. , следовательно, из формулы (4) имеем, что или .

Хорошо объясняя механизм электропроводности, классическая электронная теория проводимости не объясняет температурной зависимости сопротивления проводников. Так, экспериментально установлено, что сопротивление проводников пропорционально абсолютной температуре . Однако по классической электронной теории ; это противоречие указывает на то, что классическая теория не учитывает всех свойств электрона.

В формуле (4) величины m=const, e=const, а n и 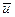практически от температуры не зависят, следовательно, зависимость удельного сопротивления от температуры может определяться лишь длиной свободного пробега электронов , т.е. обратно пропорциональна

Опыт показывает, что при и , что соответствует длине свободного пробега электронов . Поэтому можно сказать, что при абсолютном нуле температуры электроны двигаются сквозь кристаллическую решетку без столкновений, т.е. без сопротивления. С точки зрения волновой природы электрона (электрон-волна) это объясняется тем, что при Т = 0 положительные ионы металла становятся неподвижными, и электронные волны, огибая ионы, проходят через кристалл, не отклоняясь в стороны, т.е. без столкновений.

При нагревании металла узлы кристаллической решетки приходят в состояние теплового колебательного движения около положения равновесия. Чем выше температура металла, тем интенсивнее тепловые колебания узлов решетки и тем больше вероятность столкновения с ними свободных электронов. Следовательно, повышение температуры металла ведет к увеличению числа столкновений электронов с узлами решетки, и, соответственно, к уменьшению длины свободного пробега. Поэтому, в соответствии с формулой (5), нагрев металла ведет к увеличению его удельного сопротивления .

Примеси и неоднородности в кристаллической решетке металлов увеличивают их сопротивление. Это объясняется тем, что решетка образованная из различных атомов, оказывается искаженной, в силу чего увеличивается рассеяние электронов, т.е. возрастает сопротивление.

В противоположность металлам полупроводники увеличивают свою электропроводность (уменьшают удельное сопротивление) с ростом температуры, причем, как правило, в достаточно широком интервале температур возрастание происходит экспоненциально:

. (5)

Здесь постоянная Больцмана, - энергия активации электронов в полупроводнике, коэффициент пропорциональности

(в действительности зависит от температуры). С повышением температуры тепловое движение разрывает связи электронов, и часть их, пропорциональная , становится свободным носителем тока.

Связь электронов с атомами может быть разорвана не только тепловым движением, но и различными внешними воздействиями: светом, потоком быстрых частиц, сильным электрическим полем и т.д. Поэтому для полупроводников характерна высокая чувствительность электропроводности к внешним воздействиям, а также к содержанию примесей и дефектов в кристаллах.

Свойства полупроводников хорошо объясняет зонная теория. Каждый электрон в атоме имеет определенное значение энергии, называемое уровнем энергии. На каждом уровне по принципу Паули может находиться не более двух электронов, отличающихся спином, то есть собственным моментом количества движения. На рис.1 схематически изображены уровни энергии электронов в изолированном атоме.

 

Рис.2(а) Рис.2(б) Рис.1

 

В твердом теле энергетическое состояние каждого электрона определяется не только взаимодействием с ядром своего атома, но и взаимодействием с другими атомами. Поэтому при образовании твердого тела из N атомов каждый энергетический уровень изолированного атома расщепляется на N близко расположенных друг от друга уровней (рис.2 б), причем расщепление возрастает по мере сближения атомов, т.е. с уменьшением r. Совокупность этих уровней образует полосу или зону разрешенных значений энергии (рис.2 а). На каждом уровне зоны может находиться не более двух электронов. Зоны разрешенных значений энергии могут иметь различное заполнение электронами и разделены зонами запрещенных значений энергии. В полупроводниках и диэлектриках верхние из заполненных разрешенных зон называются валентными, а наиболее низкие из незаполненных зонами проводимости (рис.3 и 4а).

Электроны одной разрешенной зоны под действием внешних воздействий могут переходить в другую, а также совершать переходы внутри зоны. Для перехода электрона из валентной зоны в зону проводимости необходимо затратить энергию, не меньшую ширины запрещенной зоны между ними (рис.4б).

Для перехода электрона с одного уровня на другой внутри разрешенной зоны нужно затратить весьма малую энергию, меньшую энергии кТ теплового движения. Даже при самых высоких температурах , а ширина разрешенных зон обычно порядка 1 ¸10 эВ.

Наличие электронов в зоне проводимости делает тело проводником электричества. В зависимости от степени насыщения электронами валентной зоны и от ширины запрещенной зоны могут иметь место:

1. Все уровни валентной зоны при Т = 0 К заняты. В зоне проводимости

 

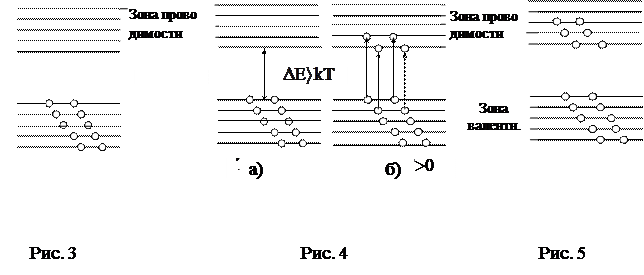
электронов нет. Ширина запрещенной зоны велика по сравнению с энергией теплового движения , т.е. (рис.3). В этом случае перевод электронов в зону проводимости возможен под действием очень сильных электрических полей или очень высоких температур.

Это- диэлектрик.

диэлектрик полупроводник металл

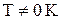2. Все уровни валентной зоны заняты. Электронов в зоне проводимости при нет. Ширина запрещенной зоны превышает величину всего в несколько десятков раз (рис.4). При такой ширине запрещенной зоны уже при комнатной температуре некоторые электроны способны перейти в зону проводимости. Поэтому, хотя при низких температурах такие твердые тела совершенно не проводят электричество, но уже при комнатной температуре приобретают проводимость.

Это - полупроводники.

3. В зоне проводимости есть электроны, занимающие при низкой температуре нижние уровни зоны. При небольшом увеличении температуры электроны легко переходят на соседние верхние свободные уровни. Валентная зона и зона проводимости могут перекрываться () или не перекрываться (). Это- металл. (Рис.5).

Электропроводность полупроводников слагается из электронной и дырочной проводимости. На схеме энергий переход электрона из валентной зоны в зону проводимости соответствует отрыву электрона от атома и переход его в свободное состояние в кристаллической решетке. Свободное от электрона место, то есть положительный ион, называется дыркой и ведет себя как положительный заряд, равный заряду электрона. Дырка может захватить электрон у соседнего атома, перескакивая на него, от него к следующему и т.д. При включении электрического поля хаотическое движение дырок и свободных электронов приобретает направленный характер. В результате электроны будут двигаться против поля, а дырки – по полю, то есть электрический ток будет обусловлен одновременно движением электронов и дырок.

Введение атомов примеси в чистый полупроводник ведет к появлению промежуточных уровней, расположенных в запрещенной зоне. Если уровни примеси заполнены электронами и расположены близко к зоне проводимости, то при повышении температуры электроны легко могут перескочить с промежуточных уровней в зону проводимости, обеспечивая тем самым электронную проводимость (рис.6).

Если уровни примеси не заполнены электронами и расположены близко к зоне заполнения, то при повышении температуры электроны из валентной зоны легко перескакивают на уровни примеси. При этом в валентной зоне образуется большое число дырок, что и обеспечивает электропроводность (рис.7), несмотря на отсутствие электронов в зоне проводимости.

Полупроводники, не имеющие примесей (атомов других элементов), являются чистыми полупроводниками. Обычно их называют полупроводниками с собственной проводимостью. Механизм электропроводности чистых полупроводников заключается в перемещении электронов против поля в зоне проводимости и дырок в валентной зоне по полю.

Важнейшей характеристикой чистых полупроводников является энергия активации - энергия, которую необходимо затратить, чтобы перевести электрон из валентной зоны в зону проводимости. Ее величина не меньше ширины запрещенной зоны.

Сопротивление полупроводников уменьшается с увеличением температуры по закону:

,

где а – const, k – постоянная Больцмана, - абсолютная температура, - энергия активации.

Причина уменьшения сопротивления полупроводников с увеличением температуры объясняется увеличением концентрации электронов в зоне проводимости, т.к. с увеличением температуры все большее число электронов переходит вследствие теплового возбуждения из валентной зоны в зону проводимости.

На использовании полупроводников основано устройство:

1. Термисторов, т.е. термосопротивлений, используемых в качестве термометров сопротивления.

2. Фотосопротивлений, фотоэлементов, фототранзисторов, фотодиодов.

3. Полупроводниковых термогенераторов.

4. Полупроводниковых лазеров.

5. Полупроводниковых выпрямителей переменного тока (диоды).

6. Полупроводниковых усилителей (триоды).

 

ВЫВОД РАБОЧЕЙ ФОРМУЛЫ.

Для определения температурного коэффициента сопротивления данного металла используется зависимость:

(6)

где - сопротивление проводника при ,

t – температура по шкале Цельсия,

- сопротивление проводника при температуре t.

Температурный коэффициент сопротивления характеризует собой относительное изменение сопротивления проводника при изменении его температуры на . Вычисляют значение по формуле:

(7)

Строго говоря, величина зависит от температуры. Поэтому из выражения (7) можно определить лишь среднее значение в интервале температур от 0 до 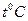. Для чистых металлов изменяется настолько незначительно, что в интервале температур порядка можно считать постоянным.

Для определения величины энергии активации данного полупроводника используется выражение:

,

откуда . (8)

График уравнения (8) в координатах изображается прямой линией (рис.8). Величина представляет собой угловой коэффициент прямой , т.е. (9)

 

Рис.8 Рис.9

 

 

Из рис.8 видно, что для двух температур Т₁ и Т₂

 

(10)

 

Сравнивая (9) и (10), получим:

 

. (11)

 

Измерение сопротивлений проводника и полупроводника при различных температурах производится с помощью моста Уитстона, схематически изображенного на рис.9. Он состоит из реохорда АС, чувствительного гальванометра G, известного и неизвестного сопротивлений. При условии отсутствия тока в мостике ВД стрелка гальванометра G станет на нуль (при замкнутом ключе К), а это значит, что потенциалы 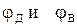точек Д и В равны, т.е. можно написать

(12)

По закону Ома для участка цепи имеем:

(13)

с учетом (13) из (12) получим:

откуда (14)

 

 

Итак, имеем: - рабочие формулы.

 

4.ОПИСАНИЕ ОПЫТНОЙ УСТАНОВКИ.

В состав опытной установки, схематически представленной на рис.10, входят: исследуемые проводник и полупроводник , эталонные сопротивления R_{э п} и R _эпп гальванометр G, выпрямитель на 6В, реохорд, переключатели К₁ и К₂, электроплитка и сосуд с водой (на схеме не указаны).

 

 

 

Рис.10

 

Исследуемые проводник 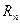и полупроводник опущены в сосуд с водой, который установлен на электроплитке. При включении электроплитки температура воды повышается, что ведет к увеличению температуры проводника и полупроводника и к изменению их сопротивлений. Измерение температуры производится термометром. Питание схемы осуществляется через выпрямитель от общего щита питания.

 

5.ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ.

1.Проверить схему установки и поставить переключатели 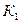и в положение “проводник”. Если температура воды более , заменить ее.

2.Тумблерами на щите питания включить электроплитку и схему установки.

3.Передвижением движка реохорда постоянно поддерживать стрелку гальванометра на нуле и при записать значения l₁ и l₂.

4.Поставить переключатель 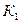и в положение “полупроводник”, движком реохорда установить стрелку гальванометра на нуль и при записать значения l₁ и l_2.

5.Повторить измерения при температурах 25°С, 30°С, 35°С, 40°С…90°С для проводника и при температурах 27°С, 32°С, 37°С…92°С для полупроводника.

6.Выключить электроплитку и установку.

 

ОБРАБОТКА ОПЫТНЫХ ДАННЫХ.

1.Для всех опытных пар значений l₁ и l₂ вычислить сопротивление проводника и полупроводника .

2.Вычислить для полупроводника значение величины .

3.Построить график зависимости сопротивления от температуры для проводника и для полупроводника

4.Пользуясь графиками, определить по рабочим формулам температурный коэффициент сопротивления проводника и энергию активации полупроводника .

5.Оценить погрешность опыта.

6.Данные опыта и расчета занести в таблицы.

- для проводника.

 

N	t (°C)	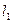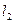(см)	(см)
…
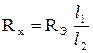
- для полупроводника
N	T (К)	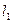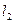(см)	(см)
...

 

 

7.КОНТРОЛЬНЫЕ ВОПРОСЫ.

1.В чем заключается сущность классической электронной теории проводимости?

2.Почему сопротивление проводников увеличивается, а полупроводников уменьшается с увеличением температуры?

3.Объясните свойства проводников и полупроводников с точки зрения зонной теории.

4.Объясните схему установки и выведите рабочие формулы.

5.Изменится ли условие равновесия моста, если гальванометр и выпрямитель поменять местами?

6.Почему гальванометр, применяемый в работе, имеет двухстороннюю шкалу с нулем посередине?

7.В чем сущность метода моста Уитстона?

Описание откорректировал ст. преподаватель

Шерстобитов И.В.___________

Зав. кафедрой доцент Горин С.В._____________

апрель 2002 г.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: