 |
Внутренние усилия. Метод сечений (Метод РОЗУ)
|
|
|
|
Nz=∑z (pi) нормальная с
Qx=∑x (pi) поперечная с
Qy=∑y (pi)
Mz=∑mz (pi) крутящий момент
Mx=∑mx (pi) изгибающий
My=∑my (pi)
Разрезаем мысл тело плоск
Отбрасываем одну из г внутр усил
Заменяем внутр усилиями
Уравновешив внутр ус внеш нагр
Правило знаков внутренних усилий
Правило знаков поперечных сил при изгибе:
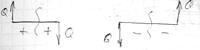
Крутящий момент
Против ЧС при взгляде со стороны сеч то +
Правило знаков изгибающих моментов:
Правило проверки правильности построения эпюр нагружения:
В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.
Эпюры внутренних усилий
ПРИ РАСТЯЖЕНИИ-СЖАТИИ
ПРИ КРУЧЕНИИ
при прямом изгибе
Дифференциальные зависимости при изгибе
; 
; 
Следствия из дифференциальных зависимостей
1. Если на участке нет распр нагр (q=0) то поперечная сила на этом участке имеет пост вел., а эпюры изгиб мом меняются по лин закону
2. На уч на котором присутст распр нагр пост интенсивн. Поперечная сила меняется по лин зак, а эпюры по закону квадр параболы. Причем эпюра мх всегда напр навстречу распр нагрузке. Где Qy равно 0 эпюра мх имеет экстремум. Если Qy равно 0 на всем участке, то мх постоян величину
4. На участке где Qy>0 эпюра мх возрастает слева направо
5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента
Понятие о напряжениях. Нормальные и касательные напряжения
Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции.
|
|
|
Выделим на плоскости сечения площадку A; по этой площадке будет действовать внутренняя сила R.
Величина отношения R/A=pср называется средним напряжением на площадке A. Истинное напряжение в точке А получим устремив A к нулю:
Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.
Очевидно, что 
. Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м2 (Па).
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
Закон парности касательных напряжений
Касат. напряжение на 2-ух взаимно перпендик. площ. направлены к ребру или от ребра и равны по величине
Понятие о деформациях. Мера линейной, поперечной и угловой деформации
Деформац – наз. взаимное перемещение точек или сечений тела по сравн с полож-ями тела которые они занимали до приложения внеш сил
бывают: упругие и пластические
а) линейная деформация
мерой явл относительное удлинение эпсила =l1-l/l
б) поперечная деф
мерой явл. относительное сужение эпсила штрих=|b1-b|/b
Гипотеза плоских сечений
Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. 
.
|
|
|
Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: 
, r — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя.
|
|
|
