Метод парабол отыскания корней уравнений

РЕФЕРАТ

 

по: Информационным технологиям

(наименование дисциплины)

Тема:Методы решения нелинейных

 

Руководитель:Коровацев А.В.

(фамилия, инициалы)

 

оценка:

 

 

Студент:Митрошкин А.В.

(фамилия, инициалы)

группа:60-102Б

 

 

подпись, дата: 07.12.2012г.

 

МОСКВА 2012

Содержание

Введение......................................................................................................................................... 3

1. Метод итераций......................................................................................................................... 4

2. Метод парабол отыскания корней уравнений....................................................................... 5

3. Метод секущих (метод хорд).................................................................................................... 9

4. Mетод Ньютона-Рафсона.......................................................................................................... 9

5. Метод половинного деления.................................................................................................. 11

Заключение.................................................................................................................................. 12

Список литературы..................................................................................................................... 13

 

Введение

При решении практических задач часто приходится составлять и решать уравнения. Любое уравнение с одним неизвестным можно представить в виде φ (x)=q(x). φ(x) и q(x) определены на некотором числовом множестве х, называемом областью допустимых значений уравнения. Уравнение обычно преобразуют к общему виду f(x)=0.

Совокупность значений переменных х, при котором уравнение f(x)=0 превращается в тождество, называется решением данного уравнения, а значение х – корнем данного уравнения.

Решить уравнение, значит найти множество всех корней этого уравнения. Если функция f(x) содержит тригонометрические, показательные, логарифмические и другие функции, то уравнение называется трансцендентным

Найти точное значение корней нелинейных уравнений можно только в исключительных случаях.

Задача нахождения корней уравнения считается решенной, если корни вычислены с заданной точностью.

Процесс нахождения приближенных значений корней уравнения разбивается на два этапа: отделение корней и уточнение корней.

В реферате рассмотрены методы решения нелинейных уравнений: метод простой итерации, парабол, секущих, Ньютона-Рафсона, деления отрезка пополам.

Метод итераций

Составим программу на Паскале. program iter; var a,e,x,xo:real; n:integer; function FunX(var m:real):real; begin funX:= ЗДЕСЬ ФУНКЦИЯ; //функция f(x) end; begin write ('Введите точность определения корня:'); readln (e); write ('Введите первое приближение x0:'); readln (x0); x:=x0; while ABS(FunX (x))>e do x:=funX(x); writeln ('Ответ: x=', xp:9:4); end.

При решении нелинейного уравнения методом итераций необходимо преобразовать уравнение к виду x=f(x). Необходимо задать начальное значение аргумента x₀ и точность ε. Первое приближение решения x₁ находим из выражения: x₁=f(x₀), второе - x₂=f(x₁) и т.д. В общем случае (i+1)-е приближение найдем по формуле x_i+1 =f(x_i). Указанную процедуру повторяем пока выполняется условие |f(xi)|>ε. Условие сходимости метода итераций |f'(x)|<1. То есть, первая производная на искомом отрезке по модулю должна быть меньше единицы. На рисунке 1 представлена блок-схема метода.

Рис. 1. Блок схема метода простых итераций

Метод парабол отыскания корней уравнений

Исходя из некоторых трех точек z 0, z 1, z 2 строится интерполяционный полином Лагранжа второй степени (парабола). Один из корней этого полинома zi выбирается в качестве приближения, и организуются новые три точки (z 0, z 1, zi). По ним опять строится полином и определяются его корни. Доказано, что такая последовательность сходится к корню уравнения (1).

Метод парабол предназначен для приближенного решения уравнения вида f(z)= 0, (1), где f(z) - заданная функция, позволяет находить все корни уравнения (1) без знания их начальных приближений (см. рис. 2). аналитический вид не требуется.

 

 

 

Рис. 2.

Полином L ₂(z) для i -го приближения имеет вид

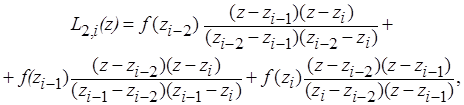(2)

где .

Точка z _{i+ 1} определяется как ближайший к z_i корень уравнения 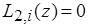. Для более удобной формы записи введем обозначения:

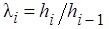, , , , , (i = 2, 3,…). (3)

Тогда соотношение (2)относительно новой переменной l запишется так:

(4)

Корни квадратного трехчлена (4) относительно l будут иметь следующий вид:

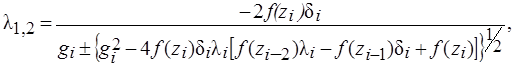(5)

где .

 

В (5) знак перед фигурной скобкой, чтобы модуль знаменателя был наибольшим, тогда

. (6)

При реализации на ЭВМ точность определения корня уравнения задается по формуле

, (7)

где e - наперед заданное положительное число, определяющее требуемую точность вычислений.

Сходимость метода парабол доказана, если начальные значения z ₀, z ₁, z ₂ находятся в достаточно малой окрестности корня уравнения (1). После того, как найден корень уравнения, требуется его выделить и приступить к отысканию следующего. Эту процедуру можно осуществить с помощью неявной схемы Горнера. Для определения второго корня уравнения, вместо исходного уравнения (1), рассматривается ,

где z ₁ - первый корень уравнения, затем

,

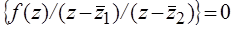и так далее.

Укажем очевидные преимущества метода парабол:

1. Не требуется знание начальных приближений корней.

2. В методе необходимо вычислять только значения функции (большинство методов требуют вычисления производных).

3. Если приближение выбрано симметрично относительно начала координат, то корни определяются в порядке возрастания.

Алгоритм метода парабол дан в виде блок-схемы (рис. 3).

 

Рис. 3. Блок – схема алгоритма метода парабол

 

Поделиться:

Воспользуйтесь поиском по сайту: