Критерии прочности и пластичности

Напряжения в точке. Главные напряжения и главные площадки.

 

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние сипы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют их смещению. Расположенная в данной точке частица по-разному взаимодействует с каждой из соседних частиц. Поэтому в общем случае в одной и той же точке напряжения различны по различным направлениям.

В сложных случаях действия сил на брус (в отличие от растяжения или сжатия) вопрос об определении наибольших напряжений, а также положения площадок, на которых они дей­ствуют, усложняется. Для решения этого вопроса приходится специально исследовать за­коны изменения напряжений при изменении положения площадок, проходящих через данную точку. Возникает проблема исследования напряженного состояния в точке деформируемого тела.

Напряженное состояние в точке - совокупность напряжений (нормальных и касательных), действующих по всевозможным площадкам (сечениям), проведенным через эту точку.

Изучение напряженного состояния дает возможность анализировать прочность материала для любого случая нагружения тела.

 

 

Рис. 5.1

 

Исследуя напряженное состояние в данной точке деформируемого тела, в ее окрестно­сти выделяют бесконечно малый (элемен­тарный) параллелепипед, ребра которого направлены вдоль соответствующих координатных осей. При действии на тело внешних сил на каждой из граней элемен­тарного параллелепипеда возникают на­пряжения, которые представляют нормаль­ными и касательными напряжениями проекциями полных напряжений на коор­динатные оси (рис. 5.1).

Нормальные напряжения обозначают буквой σ с индексом, соответствующим нормали к площадке, на которой они действуют. Касательные напряже­ния обозначают буквой τ с двумя индексами: первый соответствует нормали к площадке, а второй - направлению самого напряжения (или наоборот).

Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов напря­жения. Их можно записать в виде следующей квадратной матрицы:

σ_х τ_ху τ_хz

Т_σ = τ_уx σ_у τ_уz

τ_zx τ_zу σ_z

 

Эта совокупность напряжений называется тензором напряжений.

Тензор напряжений полностью описывает напряженное состояние в точке, то есть если известен тензор напряжений в данной точке, то можно найти напряжения на любой из площадок, проходящих через данную точку (заметим, что тензор представляет собой особый математический объект, компоненты которого при повороте координатных осей подчиняются специфическим правилам тензорного преобразования, при этом тензорное исчисление составляет отдельный раздел высшей математики и здесь не рассматривается).

Используем принятое правило знаков для напряжений в общем виде. Нормальное напряжение σ считается положительным, если совпадает по направлению с внешней нормалью к площадке, касательные напряжения τ считаются положительными, если вектор касательных напряжений следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью (рис. 5.2). Отрицательными считаются напряжения обратных направлений.

 

 

Рис. 5.2

 

Не все девять компонентов напряжений, действующих на гранях параллеле­пипеда, независимые (несвязанные друг с другом). В этом легко убедится, составив уравнения равновесия элемента в отношении его вращений относи­тельно координатных осей. Записав уравнения моментов от сил, действую­щих по граням параллелепипеда, и пренебрегая их изменением при переходе от одной грани к другой ей параллельной, получим, что

τ_ху = τ_ух, τ_хz = τ_zх, τ_yz = τ_zy (5.1)

Данные равенства называют законом парности касательных на­пряжений.

Закон парности касательных напряжений: по двум взаимно перпендикуляр­ным площадкам касательные напряжения, перпендикулярные линии пересе­чения этих площадок, равны между собой.

Закон парности касательных напряжений устанавливает зависимость между величинами и направлениями пар касательных напряжений, действующих по взаимно перпендикулярным площадкам элементарного параллелепипеда.

В окрестности исследуемой точки можно выделить бесконечное множество взаимно перпендикулярных площадок. В том числе можно найти и такие площадки, на которых действуют только нормальные напряжения, а каса­тельные напряжения равны нулю. Такие площадки называют главными (более точно – площадки главных напряжений).

Рассмотрим две взаимно перпендикулярные площадки с касательными напряжениями τ_ху и τ_ух. Согласно закону парности касательных напряжений эти напряжения равны. Поэтому, если площадку с напряжением τ_ху поворачивать до совпадения с площадкой с напряжением τ_ух, то обязательно найдется такое положение площадки, когда касательное напряжение τ = 0.

Главные площадки - три взаимно перпендикулярные площадки в окрестно­сти исследуемой точки, на которых касательные напряжения равны нулю.

Главные напряжения - нормальные напряжения, действующие по главным площадкам (то есть площадкам, на которых отсутствуют касательные напряжения).

Главные напряжения обозначаются σ₁, σ₂, σ₃, причем σ₁ ≥ σ₂ ≥ σ₃ .

На главных площадках нормальные напряжения (главные напряжения) принимают свои экстремальные значения – максимум σ₁, минимум σ₃ .

Тензор напряжений, записанный через главные напряжения, принимает наиболее простой вид:

σ₁ 0 0

Т_σ = 0 σ₂ 0

0 0 σ₃

 

В зависимости от того, сколько главных напряжений действует в окрестности данной точки, различают три вида напряженного состояния:

1) линейное (одноосное) - если одно главное напряжение отлично от нуля, а два других равны нулю (σ₁ ≠0, σ₂ = 0, σ₃ = 0);

2) плоское (двухосное) - если два главных напряжения отличны от нуля, а одно равно нулю (σ₁ ≠0, σ₂ ≠ 0, σ₃ = 0);

3) объемное (трехосное) - если все три главных напряжения отличны от нуля (σ₁ ≠0, σ₂ ≠ 0, σ₃ ≠ 0).

Рис. 5.3

 

Линейное напряженное состояние

Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис. 5.3, а).

Элементы, находящиеся в линейном напряженном состоянии, можно выделить в окрест­ности некоторых точек стержня, работающего на изгиб, иногда — при сложном нагружении, но главным образом на растяжение или сжатие.

 

Рассмотрим стержень, испытывающий простое растяжение (рис.5.4). Нормальные напряжения в его по­перечных сечениях определяются следующим образом:

σ₃ = = .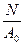

Касательные напряжения здесь равны нулю. Следовательно, эти сечения являются главными площадками (σ₁ = σ₀).

 

 

 

Рис. 5.4

 

Перейдем теперь к определению напряжений на неглавных, наклонных площадках. Выделим площадку, нормаль к которой составляет с осью стержня угол α (рис. 5.5). Проведенную таким образом наклонную площадку будем обозначать α -площадкой, а действующие на ней полные, нор­мальные и касательные напряжения - р _α, σ _α, τ_α соответственно. При этом площадь α -площадки (А _α)связана с площадью поперечного сечения стержня (А₀)следующим образом: А _α = А₀ /cos α.

Для определения напряжений воспользуемся методом мысленных сечений. Считая, что наклонная площадка рассекла стержень на две части, отбросим одну из них (верхнюю) и рассмотрим равновесие оставшейся (нижней). Осевая сила (N) в сечении представляет собой равнодействующую полных на­пряжений р _α. Следовательно,

N = р_α · А_α.

Отсюда

р _α= = 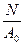cos α = σ₀ cos α.

 

 

Рис. 5.5

 

Нормальные и касательные напряжения определим, проецируя полное на­пряжение на нормаль и плоскость α -площадки соответственно:

σ _α = р _α · cos α;

τ_α = р _α · sin α,

или, учитывая, что р₀ = σ₀ cos α;

σ _α = σ₀ cos² α;

τ_α = 0,5σ₀ sin 2α.

Из анализа формул видно, что:

1) На площадках, перпендикулярных оси, касательные напряжения равны нулю (такие площадки называются главными, а действующие на них нормальные напряжения – главными нормальными напряжениями), т.е. при α = 0 в поперечных сечениях стержня τ_α = 0, σ _α = σ₀(σ₁ = σ₀, σ₂ = 0, σ₃ = 0);

2) На площадках, параллельных оси, никаких напряжений нет, поэтому это также главная площадка, т.е. при α = π / 2 в поперечных сечениях стержня τ_α = 0, σ _α = 0;

3) Наибольшие нормальные напряжения действуют в поперечных сечениях, а наибольшие касательные – на площадках, наклоненных к ним под углом 45°, т.е. при α = ± π / 4 в поперечных сечениях стержня возникают максимальные касательные напряжения τ_α = τ_max= σ₀/ 2 (нормальные напряжения σ_α = σ₀ / 2).

 

Напряжения на наклонных площадках при плоском напряженном состоянии

Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю (рис. 5.3, б).

Плоское (двухосное) напряженное состояние встречается при кручении, изгибе и сложном сопротивлении и является одним из наиболее распространенных видов напряженного со­стояния.

 

Рис. 5.6

 

Определим напряжения на наклонных пло­щадках при плоском напряженном состоя­нии. Рассмотрим элементарный параллеле­пипед, грани которого являются главными площадками (рис. 5.6). По ним действуют положи­тельные напряжения σ₁ и σ₂ , а третье глав­ное напряжение σ₃ = 0.

Проведем сечение, нормаль к которому по­вернута на угол α от большего из двух глав­ных напряжений (σ₁) против часовой стрел­ки (положительное направление α). Напря­жения σ_α и τ_α на этой площадке будут вызываться как действием σ₁. так и действием σ₂.

Запишем правила знаков. Будем считать положительными следующие направления напряжений и углов: нормальные напряжения σ — растягивающие: касательные напряжения τ — вращающие элемент по часовой стрелке: угол α — против часовой стрелки от наибольшего из главных напряжений (α < 45°).

Плоское напряженное состояние может быть представле­но как наложение (суперпозиция) двух взаимноперпендикулярных (ортогональных) одноосных напряженных состояний (рис. 5.7). При этом:

σ_α = σ_α΄ + σ_α΄΄,

τ_α = τ_α΄ + τ_α΄΄,

где σ_α΄, τ_α΄—напряжения, вызванные действием σ₁;

σ_α΄΄, τ_α΄΄ — напряжения, вызванные действием σ₂.

рис.5.7

Напряжения при одноосном напряженном состоянии (от действия Ci) связаны между собой как

σ_α΄ = σ₁ cos² α;

τ_α΄ = 0,5 σ₁ sin 2 α.

Напряжения σ_α΄΄, τ_α΄΄, вызванные действием σ₂, можно найти аналогично, но при этом необходимо учесть, что вместо угла α в формулы необходимо под­ставить угол β = — (90°— α) — угол между α -площадкой и напряжением σ₂.Отсюда получим

σ_α΄΄ = σ₂ ∙ cos²[— (90°— α)] → σ_α΄΄ = σ₂ sin² α;

τ_α΄΄ = 0,5 σ₂ sin 2[— (90°— α)] → τ_α΄΄ = - 0,5 σ₂ sin2 α;

Окончательно можем записать

σ_α = σ₁ cos² α + σ₂ sin² α = + 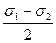cos2 α; (5.2)

τ_α = 0,5 σ₁ sin 2 α - 0,5 σ₂ sin2 α = 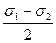sin2 α. (5.3)

Поделиться:

Воспользуйтесь поиском по сайту: