 |
Перечень учебных пособий и методических указаний
|
|
|
|
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ
Сборник заданий для контрольных работ
Направление: 09.03.01 «Информатика и вычислительная техника»
Профили: «Автоматизированные системы обработки информации и управления», «Высокопроизводительные вычислительные системы на базе больших ЭВМ», «Вычислительные машины, комплексы, системы и сети», «Системы автоматизированного проектирования»
Волгоград –2014
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Семестровая работа предполагает закрепление студентом полученных знаний по разделу “ Логические основы” курса “ Математическая логика и теория алгоритмов ”. Сборник для семестровой работы содержит 30 вариантов заданий по 11 задач в каждом, тем самым предусматривается индивидуальная работа студента. Вариант задания равен сумме трех последний цифр зачетной книжки (студенченского).
В результате выполнения работ оформляется протоколы в тонкой ученической тетради (12 или 18 листов) по правилу, рассмотренному в нижеследующем примере.
2. СБОРНИК ЗАДАНИЙ ДЛЯ СЕМЕСТРОВОЙ РАБОТЫ № 1 ПО КУРСУ «Математическая логика и теория алгоритмов»
Пример решения и оформления
| Тетрадь Для выполнения семестровой работы № 1 по курсу «Математическая логика и теория алгоритмов». Вариант 31 Выполнил: студент ФЭВТ ВолгГТУ группы ИВТ-160 Петров В.А. Дата сдачи работы: 10.12.2014 г. Проверил: Баллы: |
1. Используя таблицу истинности, установить эквивалентность функций в формуле:
Решение:
Обозначим: f1 = X1 Å X2
f2 = 
f3 = 
f4 = 
Составим таблицу истинности для правой и левой части функции:
| х1 х2 f1 |  f2  f3 f4
|
| 0 0 0 0 1 1 1 0 1 1 1 0 | 1 1 1 1 0 1 1 0 0 1 0 0 1 1 1 0 1 0 1 0 |
Ответ: Как видно из таблицы, значения правой и левой части равенства действительно совпадают, значит, функции в данной формуле эквивалентны.
|
|
|
2. Определить, какие переменные являются существенными и какие фиктивными в функции следующего вида:
f (х1,х2,х3) = (х1\/ х2) ® х 3.
Решение:
1.Необходимо составить таблицу истинности:
х1 х2 х3 х1 \/х2 (х1\/ х2) ® х3.
0 0 0 0 1
0 0 1 0 1
0 1 0 1 0
0 1 1 1 1
1 0 0 1 0
1 0 1 1 1
1 1 0 1 0
1 1 1 1 1
2.Разобьем таблицу на два подмножества: наборы для 0 значений и наборы для 1 значений:
0 1
0 1 0 0 0 0
1 0 0 0 0 1
1 1 0 0 1 1
1 0 1
1 1 1
3. Определим фиктивные и существенные переменные:
3.1. Вычеркнем первый столбец:
0 1 Видно, что есть
1 0 0 0 совпадающие
0 0 0 1 наборы, т. е.
1 0 1 1 х1 – существенная
0 1 переменная.
1 1
3.2. Вычеркнем второй столбец:
0 1 Аналогично,
0 0 0 0 х2 – существенная
1 0 0 1 переменная.
1 0 0 1
1 1
1 1
3.3. Вычеркнем третий столбец:
0 1
0 1 0 0 Аналогично,
1 0 0 0 х3 - существенная
1 1 0 1 переменная.
1 0
1 1
Ответ: х1,х2,х3 – существенные переменные.
3. Используя основные законы и соотношения алгебры логики, необходимо установить справедливость следующей формулы:
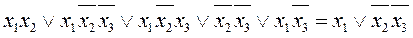
Решение:
Рекомендация: Заданное соотношение необязательно эквивалентно, поэтому необходимо перед выполнением задания проверить истинность согласно задаче № 1.
1. Проверка справедливости заданного соотношения по таблице истинности.
Если равенство неверно, основная часть задачи далее не выполняется.
Иначе
2. Необходимо левую часть равенства привести к правой части равенства.
2.1. 
2.2.. х1 
\/ х1х2 = х1 / по формуле склеивания /.
2.3. х1 \/ 
= х1 / по формуле поглощения /.
2.4. В результате в левой части равенства имеем: х1 \/ 
, что и требовалось доказать.
Ответ: соотношение в данной формуле справедливо.
4. Определить к каким классам (константы нуля, константы единицы, самодвойственных функций, монотонных функций, линейных функций, симметрических функций) относится функция следующего вида:
f(x1,x2,x3) = x1x2 \/ 
.
|
|
|
Решение:
1. Составим таблицу истинности:
х1 х2 х3 x1&x2 x3&x2 
0 0 0 0 0 1
0 0 1 0 0 1
0 1 0 0 0 1
0 1 1 0 1 0
1 0 0 0 0 1
1 0 1 0 0 1 1 1 0 1 0 1
1 1 1 1 1 0
| f(x1,x2,x3) |
2. Т. к. f (0,0,0) ¹ 0, значит, данная функция не относится к классу константы 0.
3. Т. к. f (1,1,1) = 1, значит, данная функция относится к классу константы 1.
4. Т. к. f (0,1,1) < f (0,1,0) и f (1,0,0) > f (0,1,1), значит, данная функция не относится к классу монотонных функций.
5. Т. к., например, f (0,0,0) = f (1,1,1) или f (0,0,1) = f(1,1,0), то данная функция не относится к классу самодвойственных функций.
6. Т. к. не выполняется условие f (0,1,1) = f (1,0,1) = f (1,1,0) / значения соответственно равны 0,1,1/, то данная функция не относится к классу симметрических функций.
7. Проверим принадлежность функции к классу линейных функций.
Для этого запишем ее в таком виде:
f1(x1,x2,x3) = C0 Å C1&X1 Å C2&X2 Å C3&X3.
Найдем коэффициенты Ci:
f (0,0,0) = 1 / из таблицы истинности /
С0 Å С1&0 Å C2&0 ÅC3&0 = 1, т.о., С0 = 1.
f (1,0,0)=1 / из таблицы истинности /
1 Å C1 &1 Å C 2&0 Å C 3&0 = 1, т.о., С 1 = 0.
f (0,1,0) = 1/ из таблицы истинности /
1 Å C1 &0 Å C 2&1 Å C 3&0 = 1, т.о., С 2 = 0.
f (0,0,1) = 1 / из таблицы истинности /
1 Å C 1&0 Å C 2&0 Å C 3&1 = 1,т.о., С 3 = 0.
Тогда f1(x1,x2,x3) = 1.
Сравним значения функций f и f 1 по таблице истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) 1 | f1(x1,x2,x3) |
Т. к. значения функций различны для одинаковых наборов, то данная функция не относится к классу линейных функций.
Ответ: данная функция относится к классу константы 1.
5. Необходимо для данной ФАЛ f(x1,x2,x3) найти ее ДСНФ,КСНФ,ПСНФ,ЭСНФ,ИСНФ, принимающей значение 1 на следующих наборах: 0, 4, 6, 7.
Решение:
1. Составим таблицу истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) |
2. Для получения ДСНФ, ПСНФ используем термы для 1 значений функции:
ДСНФ: f(x1,x2,x3 ) = 
ПСНФ: f(x1,x2,x3)= 
.
Для получения КСНФ, ЭСНФ используем термы для 0 значений функции:
КСНФ: f(x1,x2,x3) = 
ЭСНФ: f(x1,x2,x3) = 
4. ИСНФ:
4.1. Для получения первой формы ИСНФ 1 используем термы для 1 значений функции:
f(x1,x2,x3) = 
.
4.2. Для получения второй формы ИСНФ 0 используем термы для 0 значений функций:
f(x1,x2,x3) = 
6. Используя метод неопределенных коэффициентов, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах:
|
|
|
0, 5, 7.
Решение:
1. Составим таблицу истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) |
2.
К10 \/ К20 \/ К30 \/ К1200 \/ К1300 \/ К2300 \/ К123000 = 1
К10 \/ К20 \/ К31 \/ К1200 \/ К1301 \/ К2301 \/ К123001 = 0
К10 \/ К21 \/ К30 \/ К1201 \/ К1300 \/ К2310 \/ К123010 = 0
К10 \/ К21 \/ К31 \/ К1201 \/ К1301 \/ К2311 \/ К123011 = 0
К11 \/ К20 \/ К30 \/ К1210 \/ К1310 \/ К2300 \/ К123100 = 0
К11 \/ К20 \/ К31 \/ К1210 \/ К1311 \/ К2301 \/ К123101 = 1
К11 \/ К21 \/ К30 \/ К1211 \/ К1310 \/ К2310 \/ К123110 = 0
К11 \/ К21 \/ К31 \/ К1211 \/ К1311 \/ К2311 \/ К123111 = 1
3. Приравняем 0 все коэффициенты при 0 значениях функции:
К10 = К20 = К31 = К1200 = К1301 = К2301 = К123001 = 0
К10 = К21 = К30 = К1201 = К1300 = К2310 = К123010 = 0
К10 = К21 = К31 = К1201 = К1301 = К2311 = К123011 = 0
К11 = К20 = К30 = К1210 = К1310 = К2300 = К123100 = 0
К11 = К21 = К30 = К1211 = К1310 = К2310 = К123110 = 0.
4. Вычеркнем 0 коэффициенты из коэффициентов при 1 значениях функции:
К123000 = 1
К1311 \/ К123101 = 1
К1211 \/ К1311 \/ К123111 = 1
5. Найдем минимальное покрытие: К123000 и К1311 ,т. е.
f1(x1,x2,x3) = 
6. Проверка:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) 1 | f1(x1,x2,x3) |
Т.к. f = f1, то преобразования выполнены верно.
Ответ: f1(x1,x2,x3) =
7. Используя метод Квайна, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах: 2, 3, 4, 5, 7.
Решение:
1. Составим таблицу истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) |
2. Выпишем термы для 1 значений функции и склеим все возможные:
 *
 *
 *
 *
| 
|
3. Составим таблицу и найдем минимальное покрытие:
|
|
|
|
|
| |
|
| + | + | |||
|
| + | + | |||
|
| + |
В данном случае все импликанты являются существенными, поэтому
f1(x1,x2,x3) = \/ \/ .
Замечание: Необходимо подробно рассматривать этапы поиска существенных импликант и минимального количества покрывающих импликант (строить минимальную таблицу).
4. Проверка:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) 1 | f1(x1,x2,x3) |
Т. к. f1 = f, то преобразования выполнено верно.
Ответ: f1(x1,x2,x3) = \/ \/ .
8.Используя метод Квайна – Мак-Класки, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах:
|
|
|
2, 3, 4, 5, 6.
Решение:
1. Составим таблицу истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) |
2. Составим группы по количеству 1 и выполним необходимые преобразования:
2.1. 2.2.
1 - группа 010 100 1 - группа 01- -10 10- 1-0
2-группа 011 101 110
3. Составим таблицу и найдем минимальное покрытие:
| 01- | + | + | |||
| -10 | + | + | |||
| 10- | + | + | |||
| 1-0 | + | + |
Импликанты и являются существенными, после вычер-кивания соответствующих столбцов и строк остается один непокрытый столбец, который покрывается, например, импликантой 
.
Т. о., получаем f1(x1,x2,x3) = \/ \/ .
4. Проверка:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) 0 | f1(x1,x2,x3) |
Т.к. f1 = f, то преобразования выполнено верно.
Ответ: f1(x1,x2,x3) = \/ \/ .
9. Используя метод диаграмм Вейча, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах:
1, 2, 3, 4, 5
Решение:
1. Составим таблицу истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) |
2.
  x1
| 
| |||
| x2 | ||||
 1
| 
| |||
| x3 |
|
Получаем f1(x1,x2,x3) = \/ 
\/ .
3. Проверка:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) 0 | f1(x1,x2,x3) |
Т. к. f1 = f, то преобразования выполнено верно.
Ответ: f1(x1,x2,x3) = \/ \/ .
10. Доопределить функцию
.
Решение:
Составим таблицу истинности:
| № | 
| 
| 
| 
| 
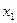
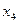
| Fопр |
| * | ||||||
| * | ||||||
| * | ||||||
| * | ||||||
| * | ||||||
| * | ||||||
| * | ||||||
| * |
1) доопрделим *=1 и получим минимальный вид функции
.
Доопрделим *=0
.
Оптимальное доопрделение функций соответствующее минимальному покрытию может быть найдено по методу Квайна.
| 
| 
| 
| |
| V | |||
| V | V | ||
| V | V | ||
| V |
В результате получится минимальный вид функции вида: 
, ее таблица единичных значений тогда будет: 
.
Ответ: (см. таблицу истинности).
11. Найти производную третьего порядка 
.
Решение:
.
.
.
.
.
.
.
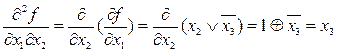Ответ:
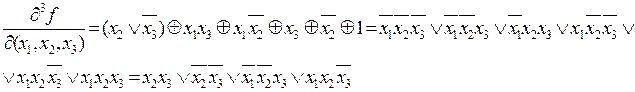
2.1. Условия задач и варианты заданий для семестровой работы.
Условия задач / общие для всех вариантов/
1. Используя таблицу истинности, установить эквивалентность функций в формуле.
|
|
|
2. Определить, какие переменные являются существенными и какие фиктивными в функции следующего вида.
3. Используя основные законы и соотношения алгебры логики, необходимо установить справедливость следующей формулы.
4. Определить к каким классам (константы нуля, константы единицы, самодвойственных функций, монотонных функций, линейных функций, симметрических функций) относится функция следующего вида.
5. Необходимо для данной ФАЛ f(x1,x2,x3,x4) найти ее ДСНФ, КСНФ, ПСНФ, ЭСНФ, ИСНФ, принимающей значение 1 на следующих наборах.
6. Используя метод неопределенных коэффициентов, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах.
7. Используя метод Квайна, необходимо найти МДНФ функции f(x1,x2,x3,x4), принимающей значение 1 на наборах.
8.Используя метод Квайна- Мак - Класки, необходимо найти МДНФ функции f(x1,x2,x3,x4), принимающей значение 1 на наборах.
9.Используя метод диаграмм Вейча, необходимо найти МДНФ функции f(x1,x2,x3,x4), принимающей значение 1 на наборах.
10. Доопределить функцию f(x1,x2,x3,x4).
11. Найти производную третьего порядка f(x1,x2,x3).
Варианты заданий для семестровой работы
Вариант 1
1. 
.
2. 
.
3. 
.
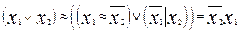4. 
.
5. 0, 2, 4, 6, 8, 9, 11, 12, 14, 15.
6. 0, 2, 4, 6.
7. 1, 2, 6, 7, 9, 12, 13.
8. 1, 6, 7, 8, 9, 10, 11, 12, 13.
9. 3, 8, 9, 10, 12, 13, 15.
10. 1, 6*, 7, 8, 9*, 10, 11*, 12, 13.
11. 
Вариант 2
1. 
.
2. 
.
3. 
.
4. 
.
5. 0, 1, 2, 6, 7, 8, 12, 13, 14.
6. 1, 3, 5, 7.
7. 2, 3, 5, 6, 10, 11, 14, 15.
8. 3, 6, 7, 8, 10, 11, 14.
9. 0, 5, 8, 9, 10, 12, 13, 15.
10. 0, 5, 8, 9, 10*, 12*, 13*, 15*.
11. 
Вариант 3
1. 
.
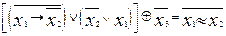2. 
.
3. 
.
4. 
.
5. 4, 6, 8, 9, 11, 12.
6. 0, 1, 3, 4.
7. 1, 2, 3, 7, 11, 13, 14, 15.
8. 6, 8, 9, 12, 13, 14.
9. 0, 8, 10, 11, 13, 15.
10. 1, 2, 3, 7*, 11*, 13*, 14, 15*.
11. 
.
Вариант 4
1. 
.
2. 
.
3. 
.
4. 
.
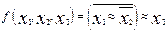5. 0, 1, 2, 3, 6, 12.
6. 2, 3, 6, 7.
7. 2, 3, 4, 5, 10, 12, 13, 15.
8. 6, 7, 8, 10, 11, 13.
9. 1, 2, 3, 12, 13, 14, 15.
10. 1, 2, 3, 12, 13*, 14, 15*.
11. 
.
Вариант 5
1. 
.
2. 
.
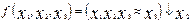3. 
.
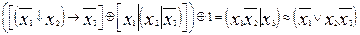4. 
.
5. 0, 6, 10, 14.
6. 0, 1, 2, 5, 6, 7.
7. 2, 4, 6, 9, 10, 11, 12, 13.
8. 5, 6, 7, 8, 9, 13, 14.
9. 2, 3, 7, 8, 10, 11, 12, 15.
10. 2, 3, 7, 8, 10*, 11*, 12, 15*.
11. 
.
Вариант 6
1. 
.
2. 
.
3. 
.
4. 
.
5. 1, 5, 6, 7, 8, 14.
6. 3, 4, 7.
7. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13.
8. 2, 4, 5, 6, 8, 11, 12, 14.
9. 0, 4, 6, 7, 8, 10, 13, 15.
10. 0, 4, 6, 7, 8*, 10, 13*, 15.
11. 
.
Вариант 7
1. 
.
2. 
.
3. 
.
4. 
.
5. 0, 1, 4, 5, 7, 9.
6. 0,1,2,3,4.
7. 0, 2, 3, 5, 7, 8, 10, 11, 15.
8. 2, 3, 5, 6, 7, 8, 10, 12, 14.
9. 0, 4, 5, 7, 8, 10, 11, 13, 15.
10. 0, 2, 3*, 5, 7*, 8, 10*, 11, 15.
11. 
.
Вариант 8
1. 
.
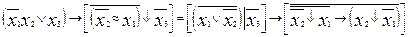2. 
.
3. 
.
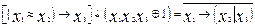4. 
.
5. 6, 7, 8, 9, 10, 11.
6. 1, 2, 5, 7.
7. 0, 3, 7, 8, 11, 13, 14, 15.
8. 2, 3, 4, 5, 12, 13, 14.
9. 0, 4, 5, 6, 7, 14, 15.
10. 0, 3, 7, 8, 11, 13*, 14, 15*.
11. 
.
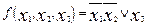Вариант 9
1. 
.
2. 
.
3. 
.
4. 
.
5. 1, 2, 4, 7, 8, 11, 13, 14.
6. 1, 2, 4.
7. 0, 1, 2, 3, 8, 9, 10, 11, 14, 15.
8. 1, 2, 5, 7, 8, 12, 13, 14.
9. 2, 4, 7, 9, 10, 14, 15.
10. 0, 1, 2, 3, 8*, 9, 10, 11*, 14, 15*.
11. 
.
Вариант 10
1. 
.
2. 
.
3. 
.
4. 
.
5. 3, 7, 11, 15.
6. 0, 1, 2, 3, 4, 5, 6.
7. 4, 6, 7, 8, 9, 10, 14, 15.
8. 1, 5, 6, 7, 8, 9, 10, 15.
9. 0, 3, 7, 8, 9, 10, 11, 12, 15.
10. 1, 5*, 6, 7, 8, 9*, 10, 15.
11. 
.
Вариант 11
1. 
.
2. 
.
3. 
.
4. 
.
5. 1, 2, 3, 4, 5, 6, 7, 9, 13, 14, 15.
6. 1, 2, 3, 4, 5, 6.
7. 0, 1, 2, 3, 4, 8, 9, 10, 11, 12.
8. 0, 1, 2, 3, 9, 10, 13, 14, 15.
9. 0, 2, 3, 5, 11, 12, 15.
10. 0, 2*, 3, 5, 11, 12*, 15*.
11. 
.
Вариант 12
1. 
.
2. 
.
3. 
.
4. 
.
5. 0, 3, 4, 7, 8, 11, 12, 15.
6. 2, 3, 4, 5.
7. 1, 3, 6, 8, 9, 10, 12, 13.
8. 0, 2, 5, 6, 8, 11, 12, 13, 14.
9. 0, 2, 4, 7, 8, 10, 13, 15.
10. 0, 2, 5, 6*, 8, 11*, 12*, 13, 14.
11. 
.
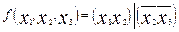Вариант 13
1. 
.
2. 
.
3. 
.
4. 
.
5. 0, 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15.
6. 0, 2, 3, 4, 5, 7.
7. 2, 5, 7, 8, 11, 12, 13, 15.
8. 1, 4, 6, 7, 10, 11, 12, 14.
9. 0, 3, 6, 8, 9, 12, 13, 15.
10. 0, 3, 6, 8, 9*, 12, 13*, 15*.
11. 
.
Вариант 14
1. 
.
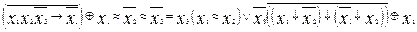2. 
.
3. 
.
4. 
.
5. 0, 1, 6, 7, 8, 9, 14, 15.
6. 0, 3, 4, 6, 7.
7. 1, 3, 6, 7, 9, 12, 13, 14, 15.
8. 0, 2, 5, 7, 8, 9, 11, 12.
9. 2, 4, 7, 9, 10, 11, 13, 15.
10. 0*, 2, 5, 7, 8, 9*, 11*, 12.
11. 
.
Вариант 15
1. 
.
2. 
.
3. 
.
4. 
.
5. 2, 3, 4, 5, 8, 9, 14, 15.
6. 0, 1, 2, 5.
7. 0, 1, 6, 7, 8, 9, 10, 11.
8. 3, 5, 6, 7, 8, 9, 13, 14.
9. 5, 7, 8, 9, 10, 11, 15.
10. 0*, 1*, 6*, 7, 8, 9, 10, 11.
11. 
.
Вариант 16
1. 
.
2. 
.
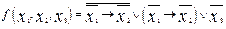3. 
.
4. 
.
5. 0, 1, 2, 3, 12, 13, 14, 15.
6. 1, 2, 3, 7.
7. 0, 1, 2, 3, 4, 10, 11, 14, 15.
8. 0, 1, 2, 3, 7, 8, 9, 10, 11, 15.
9. 2, 3, 4, 5, 9, 10, 12, 13.
10. 0, 1*, 2*, 3, 7*, 8, 9, 10, 11, 15.
11. 
.
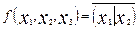Вариант 17
1. 
.
2. 
.
3. 
.
4. 
.
5. 1, 2, 4, 7, 9, 10, 13, 15.
6. 1, 2, 4, 5.
7. 2, 3, 6, 8, 9, 13, 14, 15.
8. 0, 1, 2, 7, 8, 9, 10, 13, 14, 15.
9. 2, 3, 4, 9, 10, 11, 14, 15.
10. 0, 1*, 2, 7*, 8*, 9*, 10, 13, 14, 15.
11. 
.
Вариант 18
1. 
.
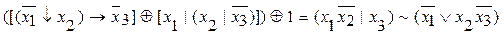2. 
.
3. 
.
4. 
.
5. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15.
6. 0, 3, 4, 7.
7. 3, 4, 5, 6, 13, 14, 15.
8. 2, 6, 7, 10,12,13 14, 15.
9. 0, 2, 4, 8, 12, 14, 15.
10. 2*, 6, 7*, 10,12,13 14, 15.
11. 
.
Вариант 19
1. 
.
2. 
.
3. 
.
4. 
.
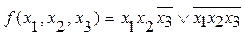5. 0, 10, 11, 12, 13, 14, 15.
6. 1, 2, 5, 6.
7. 7, 8, 9, 11, 12, 14.
8. 1, 2, 3, 4, 9, 11, 12, 14.
9. 3, 4, 5, 6, 11, 13, 15.
10. 3*, 4*, 5, 6*, 11, 13, 15.
11. 
.
Вариант 20
1. 
.
2. 
.
3. 
.
4. 
.
5. 0, 2, 4, 6, 9, 11, 13, 15.
6. 0, 1, 2, 3, 5, 6, 7.
7. 3, 5, 6, 7, 9, 12, 13, 15.
8. 3, 4, 5, 6, 7, 8, 9, 10, 11.
9. 5, 6, 7, 8, 9, 10, 11, 12, 13.
10. 5*, 6, 7*, 8*, 9, 10*, 11, 12, 13.
11. 
.
Вариант 21
1. 
.
2. 
.
3. 
.
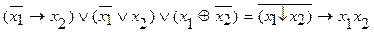4. 
.
5. 0, 1, 2, 3, 7, 11, 15.
6. 0, 1, 4, 5.
7. 2, 7, 8, 9, 10, 11, 12, 13, 14.
8. 0, 1, 5, 6, 8, 11, 12.
9. 2, 3, 7, 8, 10, 13, 14, 15.
10. 2*, 3, 7*, 8*, 10, 13*, 14, 15.
11. 
.
Вариант 22
1. 
.
2. 
.
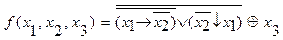3. 
.
4. 
.
5. 2, 3, 4, 5, 10, 11, 12, 13.
6. 1, 2, 4, 5, 6.
7. 3, 4, 6, 7, 8, 9, 11, 13, 15.
8. 1, 2, 4, 6, 7, 9, 10, 14, 15.
9. 2, 3, 4, 6, 8, 9, 11, 12.
10. 3*, 4*, 6, 7*, 8, 9*, 11, 13, 15.
11. 
.
Вариант 23
1. 
.
2. 
.
3. 
.
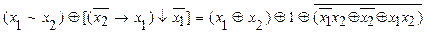4. 
.
5. 0, 2, 5, 7, 8, 10, 13, 15.
6. 1, 2, 3, 5, 6, 7.
7. 7, 9, 10, 13, 14, 15.
8. 0, 1, 2, 6, 10, 12, 13, 14.
9. 2, 3, 4, 8, 12, 14, 15.
10. 2*, 3, 4*, 8*, 12*, 14, 15.
11. .
Вариант 24
1. 
.
2. 
.
3. 
.
4. 
.
5. 0, 1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15.
6. 0, 2, 3, 4, 6, 7.
7. 4, 7, 8, 9, 11, 12, 15.
8. 1, 2, 4, 5, 9, 10, 13, 14.
9. 0, 3, 4, 6, 7, 11, 12, 15.
10. 4*, 7*, 8, 9, 11*, 12, 15.
11. 
.
Вариант 25
1. 
.
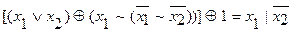2. 
.
3. 
.
4. 
.
5. 0, 4, 8, 11, 12, 13, 14, 15.
6. 0, 1, 3, 4, 6, 7.
7. 6, 7, 8, 9, 10, 14, 15.
8. 1, 3, 5, 8, 9, 10, 11, 12.
9. 3, 5, 7, 10, 11, 12, 13, 14.
10. 1*, 3, 5*, 8, 9, 10, 11, 12.
11.
