Предисловие. Оглавление. 15.1. Вариант 1

Министерство образования Российской Федерации

 

Новосибирский Государственный Технический Университет

________________________________________________________

 

 

КВАНТОВАЯ ОПТИКА

КВАНТОВАЯ МЕХАНИКА

 

 

Варианты задач индивидуальных заданий

для студентов I-II курсов ФЛА, АВТФ, ФАЭМС, ФАМ,

ФБ, ФПМ дневной формы обучения

 

 

Новосибирск

 

Составители: Э. Б. Селиванова, канд. пед. наук, доц., (тема 15-18)

       Л. М. Родникова, ассист. (тема 15)

       Н. В. Клягина, ассист. (тема 17)

       М. А. Шорохова, ассист. (тема 16)

 

 

Рецензент В. Я. Чечуев, канд. техн. наук, доц.

 

 

Работа подготовлена на кафедре общей физики

 

 © Новосибирский государственный

технический университет, 2003

 

Предисловие

 

 

В методическом пособии «Квантовая оптика. Квантовая механика» представлены 4 темы раздела курса общей физики: тема 15 – Тепловое излучение; тема 16 - Фотоэффект. Световое давление. Эффект Комптона; тема 17 – Волны де Бройля. Соотношение неопределенностей; тема 18 – Уравнение Шредингера. Одномерный бесконечный потенциальный ящик. Потенциальный барьер (низкий и высокий). Атом водорода. Молекулы (нумерация тем сквозная в первой, второй и третьей частях сборников задач).

По каждой теме подобраны 18 одинаковых по сложности вариантов специально подобранных задач. При их составлении учитывались результаты психолого-педагогического анализа процесса решения физических задач, выполненных как составителями, так и другими авторами.

В каждом варианте представлены задачи всех выделенных в данной теме типов; кроме того, присутствуют задачи на развитие образных компонентов мышления (графические задачи, при решении которых используется перевод с «языка» формул на «язык» образов и наоборот).

Более подробно о типах задач можно прочитать в методических указаниях к решению задач в курсе общей физики «Квантовая оптика» (составители: Селиванова Э. Б., Чечуев В. Я., 1999 г. ). В них в краткой наглядной форме (в виде таблиц) изложена теория, даны определения основных физических понятий, приведены соотношения между ними, указаны методы и разобраны примеры решения всех типов, выделенных в теме.

На основе приведенной теории и примеров могут быть решены и задачи других вариантов.

Настоящая работа может быть использована на практических занятиях, при выполнении индивидуальных и контрольных заданий, а также на экзаменах.

 

Канд. пед. наук, доц.

чл. -корр. МААН                                                            Селиванова Э. Б.

 

Оглавление

 

1. Предисловие........................................................................

 

2. Тема 15. Тепловое излучение (варианты 15. 1–15. 18).......

3. Тема 16. Фотоэффект. Световое давление. Эффект

         Комптона (варианты 16. 1–16. 18).............................

4. Тема 17. Волны де Бройля. Соотношение неопределен-

         ностей (варианты 17. 1–17. 18)..................................

5. Тема 18. Уравнение Шредингера. Одномерный бесконеч-

        ный потенциальный ящик. Потенциальный барьер

        (низкий и высокий). Атом водорода. Молекулы.

        (варианты 18. 1-1818).................................................

6. Приложение.........................................................................

 

15. Тема. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ

15. 1. Вариант 1

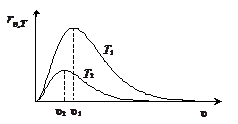· 15. 1. 1. На рисунке показаны графики зависимости испускательной способности серого тела от частоты излучения при двух разных температурах T₁ и Т₂. Изобразите аналогичные графики для абсолютно черного тела при тех же температурах. Сравните энергетические светимости этих тел при указанных температурах.

· 15. 1. 2. Вольфрамовая нить нагревается в вакууме током силой I₁ = 1, 0 А до температуры T₁ = 1000 К. При какой силе тока нить накалится до температуры T₂ = 3000 К? Коэффициенты излучения вольфрама и его удельные сопротивления, соответствующие температурам T₁ и T₂, равны: = 0, 115; = 0, 33; r₁ = 25, 7·10^-8 Ом·м; r₂ = 96, 6·10^–8 Ом·м.

· 15. 1. 3. Поток излучения абсолютно черного тела Ф = 10 кВт. Максимум энергии излучения приходится на длину волны l_m = 0, 8 мкм. Определите площадь S излучающей поверхности.

· 15. 1. 4. Расстояния между Солнцем и планетами Земля и Венера соответственно равны: r₁ = 1, 5·10⁸ км, r₂ = 1, 1·10⁸ км. Средняя температура поверхности Земли t = 20 ⁰С. Принимая Солнце и указанные планеты за абсолютно черные тела, оцените среднюю температуру поверхности Венеры.

· 15. 1. 5. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, l_m = 0, 55 мкм. Определите энергетическую светимость R_Э поверхности тела, а также спектральную излучательную способность r_{l, T}, соответствующую длине волны l_m.

15. 2. Вариант 2

· 15. 2. 1. Два тела одинаковой формы и размеров, но обладающие разной поглощательной способностью, нагреты до одинаковой температуры, а затем помещены в вакуум. В результате излучения эти тела остывают. Кривые на рисунке показывают изменение температуры тел в процессе остывания. По оси абсцисс отложено время остывания от момента помещения тел в вакууме, а по оси ординат – температуры тел. Какая из кривых характеризует остывание тела с большей поглощательной способностью, какая – с меньшей?

 

 

· 15. 2. 2. Определите поглощательную способность серого тела, имеющего температуру Т = 1·10³ К, если его поверхность с площадью S = 1·10^-2 м² излучает за время t = 1 мин энергию E = 13, 4 кДж.

· 15. 2. 3. Длина волны, на которую приходится максимум испускательной способности абсолютно черного тела, уменьшается в два раза. Как при этом изменяется площадь, ограниченная графиком функции распределения плотности энергии равновесного излучения по длинам волн?

· 15. 2. 4. Излучение Солнца по своему спектральному составу близко к излучению абсолютно черного тела, для которого максимум испускательной способности приходится на длину волны l_m = 0, 48 мкм. Найдите массу, теряемую Солнцем ежесекундно за счет излучения. Оцените время, за которое масса Солнца уменьшится на 1 %.

· 15. 2. 5. Определите длину волны, на которую приходится максимальное значение испускательной способности абсолютно черного тела, равное 6·10¹¹ Вт·м^–2·м^–1.

15. 3. Вариант 3    

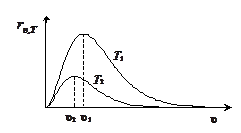· 15. 3. 1. На рисунке изображены графики зависимости испускательной способности абсолютно черного тела от частоты при двух разных температурах. Сравните температуры Т₁ и Т₂. Изобразите аналогичные зависимо-сти для серого тела при тех же температурах.

· 15. 3. 2. Пластинка с черной поверхностью помещена перпендикулярно падающим лучам в вакууме. Определите энергию Е, поглощаемую 1 см² поверхности за время t = 1 мин, если температура поверхности пластинки Т установилась равной 500 К.

· 15. 3. 3. Максимум излучения полого излучателя приходится на длину волны 0, 58 мкм. Определите лучистый поток, испускаемый излучателем, если площадь его поверхности равна 4 см².

· 15. 3. 4. Тело массой m = 10 г и поверхностью S = 200 см², имеющее температуру Т₀ = 600 К, помещено в вакуум. Определите, до какой температуры Т охладится тело за время t = 30 с, если поглощательная способность поверхности тела = 0, 4, а удельная теплоемкость С = 350 Дж·кг^–1·К^–1.

· 15. 3. 5. Длина волны, соответствующая максимуму излучения для Полярной звезды, = 0, 35 мкм, а для Сириуса = 0, 29 мкм. Вычислите температуру поверхностей этих звезд и сравните их интегральные и спектральные излучения за 1 с
с единичной поверхности звёзд, считая их абсолютно черными телами вблизи данной длины волны.

15. 4. Вариант 4

· 15. 4. 1. На графике, представляющем универсальную функцию Кирхгофа, выделены два участка, площади которых равны. Одинаково ли число квантов энергии, излучаемых в указанных интервалах длин волн абсолютно черным телом, имеющим данную температуру?

jl, Т

 

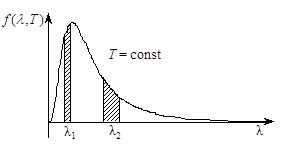
· 15. 4. 2. Диаметр вольфрамовой спирали в электрической лампочке d = 0, 3 мм, длина спирали = 5 см. При напряжении 127 В через лампочку течет ток силой 0, 31 А. Найдите температуру спирали, считая, что при достигнутом равновесии энергия теряется только за счет теплового излучения. Коэффициент поглощения вольфрама при этой температуре = 0, 3.

· 15. 4. 3. При нагревании абсолютно черного тела длина волны, на которую приходится максимум излучательной способности, изменилась от = 0, 69 мкм до 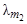= 0, 5 мкм. Как и во сколько раз изменилась при этом энергетическая светимость тела?

· 15. 4. 4. Найдите солнечную постоянную I, т. е. количество лучистой энергии, посылаемой Солнцем в единицу времени через единичную площадку, расположенную перпендикулярно солнечным лучам и находящуюся на таком же расстоянии от Солнца, как и Земля. Температура поверхности Солнца Т = 5800 К. Излучение Солнца считайте близким к излучению абсолютно черного тела (r _С-З = 1, 5·10⁸ км).

· 15. 4. 5. Температура абсолютно черного тела равна 2000 К. Определите: а) испускательную способность для длины волны l = 600 нм; б) энергетическую светимость в интервале длин волн от l₁ = 590 нм до l₂ = 610 нм. Примите, что среднее значение испускательной способности тела в этом интервале равно значению, найденному для l = 600 нм.

15. 5. Вариант 5

· I5. 5. 1. Нa рисунке показаны зависимости поглощательной способности некоторых тел, имеющих одинаковую температуру, от длины волны излучения. Изобразите зависимости испускательной способности от длины волны для этих тел при той же температуре. Сравните энергетические светимости тел.

 

· 15. 5. 2. Для повышения температуры верхнего слоя почвы ее поверхность покрыли угольным порошком, в результате чего установилась температура, равная 27 ^оС. Определите энерге-тическую светимость угольной мульчи, принимая ее за серое тело, если ее поглощательная способность при данной температуре равна 0, 88.

· 15. 5. 3. Оцените установившуюся температуру абсолютно черной пластины, находящейся в вакууме и расположенной перпендикулярно потоку лучистой энергии, равному 1, 4·10³ Вт/м². Определите, на какую длину волны приходится максимум спектральной плотности энергетической светимости при данной температуре.

· 15. 5. 4. Считая Солнце абсолютно черным телом, найдите уменьшение массы Солнца за 1 год вследствие излучения. Температуру поверхности Солнца примите равной 5800 К.

· 15. 5. 5. Найдите максимальное значение испускательной способности абсолютно черного тела, если оно соответствует длине волны l = 1, 45 мкм.

15. 6. Вариант 6

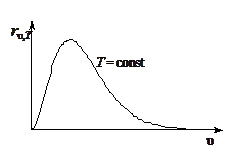· 15. 6. 1. На рисунке изображен график зависимости излуча-тельной способности абсолютно черного тела от частоты излучения при температуре Т. Как, поль-зуясь гpaфиком, определить энергетическую свeтимость серого тела, если поглоща-тельная способность при данной температуре равна

· 15. 6. 2. Температура вольфрамовой спирали электрической лампы мощностью 75 Вт равна 2500 К. Поглощательная способность вольфрама при данной температуре равна 0, 3. Найдите площадь излучающей поверхности, приняв спираль за серое тело.

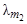· 15. 6. 3. Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра ( = 780 нм) на фиолетовую ( = 390 нм)?

· 15. 6. 4. Определите, за какое время медный шар, помещенный в вакуум, охладится с Т₁ = 500 К до Т₂ = 300 К. Радиус шара R = 1 см, поглощательная способность поверхности = 0, 8, удельная теплоемкость меди С = 0, 094 Kал·г^-1·К^–1, плотность r = 8, 9 г. см^–3. Излучением окружающих предметов пренебречь.

· 15. 6. 5. Температура абсолютно черного тела изменилась при нагревании от 1000 К до 3000 К. Найдите изменение при этом длины волны, на которую приходится максимум испускательной способности тела? Как и во сколько раз изменилось значение максимальной испускательной способности?

 

15. 7. Вариант 7         

·

jl, T

15. 7. 1. На графи-ке, представляющем универсальную функ-цию Кирхгофа, выде-лены два узких участ-ка, площади которых равны. Одинаковы ли для абсолютно черного тела на указаных дли-нах волн l₁ и l₂:

а) испускательная способность r _{l, T};

б) энергетическая светимость ∆ R _{l, T.}

· 15. 7. 2. Температура абсолютно черного тела возросла от Т₁ = 500 К до Т₂ = 1500 К. Во сколько раз увеличилась энергия, испускаемая единицей поверхности тела в единицу времени?

· 15. 7. 3. Определите длину волны, на которую приходится максимум энергии в спектре звезды с температурой 30 000 К. Чему равна энергетическая светимость такой звезды?

· 15. 7. 4. Пренебрегая потерями тепла на теплопроводность, определите мощность Р электрического тока, необходимую для накаливания нити диаметром d = 1 мм и длиной  до температуры 3500 К.

· 15. 7. 5. Если температура абсолютно черного тела уменьшилась с Т₁ = 2500 К до Т₂ = 1000 К, то как и во сколько раз изменилась его энергетическая светимость и максимальное значение испускательной способности?

15. 8. Вариант 8

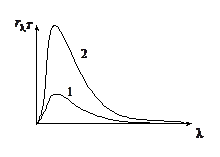· 15. 8. 1. На рисунке приведены зависимости испускательной способности от длины волны излучения для двух тел, одно из которых является аб-солютно черным. Тем-пература тел одина-кова. Все ординаты первого графика в 3 раза меньше ординат второго. Изобразите зависимости поглоща-тельных способностей этих тел от длины волны.

· 15. 8. 2. Вычислите ис-тинную температуру Т воль-фрамовой раскаленной ленты, если радиационный пирометр показывает температуру Т_р = 2, 5 К. Примите, что коэффициент излучения вольфрама не зависит от частоты излучения = 0, 35.

· 15. 8. 3. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела l_m = 0, 58 мкм. Определите энергетическую светимоcть Rэ поверхности тела.

· 15. 8. 4. Температура поверхности Солнца Т = 5600 К. Считая, что поглощательная способность Солнца и Земли равна единице, оцените среднюю температуру поверхности Земли (r _С-З = 1, 5·10⁸ км).

· 15. 8. 5. Температура абсолютно черного тела равна 3000 К. Определите энергетическую светимость абсолютно черного тела в интервале длин волн oт l₁ = 600 нм до l₂ = 620 нм, рассчитав среднее значение испуокательной способности тела в этом интервале, соответствующее l = 610 нм.

15. 9. Вариант 9

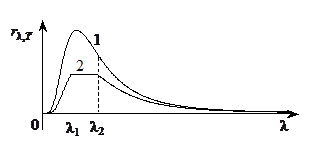
· 15. 9. 1. На рисунке изображено распределение энергии в спектре излучения абсолютно черного тела (кривая 1) и при той же температуре для некоторого условного тела в схематизированном виде. Все ординаты кривой 2 вдвое меньше ординат кривой 1 на участках 0 < l< l₁, l₂ < l < ¥, а для участка l = l₁¸ l₂ остаются постоянными. Нарисуйте распределение по длинам волн поглощательной способности условного тела.

 

 

· 15. 9. 2. Поглощательная способность вольфрама при Т = 2000 К равна 0, 26. Какая мощность электрического тока необходима для поддержания такой температуры нити лампы радиопередатчика, если площадь поверхности нити равна 0, 001 м²?

· 15. 9. 3. Какое количество энергии с 1 см² поверхности излучает абсолютно черное тело за 1 с, если известно, что длина волны, на которую приходится максимум его излучательной способности при этой температуре, равна 7·10^–5 см?

· 15. 9. 4. На небольшой плоский диск радиусом R = 0, 1 м, находящийся в вакууме на среднем расстоянии от Земли до Солнца, излучение падает почти нормально. Считая диск и Cолнце абсолютно черными телами, определите температуру диска. Температура поверхности Солнца Т_С = 6000 К
(r _С-З = 1, 5·10⁸ км).

· 15. 9. 5. Вследствие изменения температуры абсолютно черного тела максимум испускательной способности сместился с 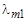= 2, 4 мкм на = 0, 8 мкм. Как и во сколько раз изменились интегральная и максимальная спектральная излучательная способности тела?

15. 10. Вариант 10   

· 15. 10. 1. Как, учитывая представленный на рисунке график универсальной функции Кирх-гофа, определить энергети-ческую светимость при одной и той же температуре для абсолютно черного тела и серого тела, имеющего погло-щательную способность, равную ?

· 15. 10. 2. Из смотрового окошечка печи излучается поток Ф = 4 кДж/мин. Определите температуру Т печи, если площадь окошечка S = 8 см².

· 15. 10. 3. Определите, как изменится энергетическая светимость абсолютно черного тела, если длина волны, на которую приходится максимум испускательной способности, увеличится в 1, 5 раза.

· 15. 10. 4. Поверхность Солнца близка по своим свойствам к абсолютно черному телу. Максимум испускательной способности приходится на длину волны l_m = 0, 50 мкм (в излучении Солнца, прошедшем через атмосферу и достигнувшем поверхности Земли, максимум приходится на l = 0, 55 мкм). Определите:
а) температуру поверхности Солнца; б) энергию, излучаемую Солнцем за 1 с в виде электромагнитных волн.

· 15. 10. 5. Температура абсолютно черного тела Т = 2000 К. Оцените, какая доля излучаемого потока энергии приходится на видимую часть спектра излучения.

15. 11. Вариант 11

· 15. 11. 1. На рисунке изображен график зави-симости испускательной способности серого тела, имеющего при данной тем-пературе поглощательную способность . Как, поль-зуясь графиком, определитъ энергетическую светимость абсолютно черного тела при той же температуре?

· 15. 11. 2. Для профилактики иссушения верхнего слоя почвы вследствие перегрева поверхность почвы покрывают молотым мелом (мульчируют). Определите поглощательную способность мульчи, принимая её за серое тело, если энергетическая светимость ее при температуре Т = 300 К равна 64 Вт/м².

· 15. 11. 3. Вследствие повышения температуры максимум излучательной способности абсолютно черного тела переместился с 2 мкм до 1 мкм. Во сколько раз изменилась энергетическая светимость тела?

· 15. 11. 4. До какого значения понизилась бы температура земного шара за столетие, если бы на Землю не поступала солнечная энергия? Радиус Земли примите равным 6, 4·10⁶ м, удельную теплоемкость 200 Дж·кг^-1·К^–1, плотность 5500 кг/м³, среднюю температуру поверхности 280 К, поглощательную способность а _Т = 0, 8.

· 15. 11. 5. Максимальное значение испускательной способности абсолютно черного тела равно 4, 16·10¹¹ Вт/м². На какую длину волны оно приходится?

15. 12. Вариант 12 

·

jl, Т

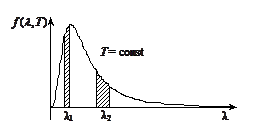15. 12. 1. В энергетическом распределении излучения абсолютно черного тела выделены два участка, площади которых одинаковы. Одинаковы ли мощности излучения, приходящиеся на соответствующие интервалы длин волн (ответ поясните) и одинаково ли число излучаемых квантов энергии за единицу времени?

·

jl, Т

15. 12. 2. Как из-менится общее ко-личество энергии, из-лучаемой телом в единицу времени, если температура одной его половины увеличилась в два раза, а другой – уменьшилась в два раза по сравнению с первоначальным состоянием. Тело считается абсолютно черным.

· 15. 12. 3. Энергетическая светимость абсолютно черного тела R_э = 3 Вт/см². Определите длину волны l_m, соответствующую максимуму испускательной способности тела.

· 15. 12. 4. Через какое время масса Солнца уменьшилась бы вдвое за счет теплового излучения, если бы мощность его оставалась постоянной? Температуру поверхности Солнца примите равной 5800 К и Солнце считайте абсолютно черным телом.

· 15. 12. 5. Вычислите, во сколько раз увеличится энергетическая светимость абсолютно черного тела в небольшом интервале длин волн вблизи l = 5 мкм при повышении температуры от Т₁ = 1000 К до Т₂ = 2000 К.

15. 13. Вариант 13

· 15. 13. 1. На рисунке изображен график универсальной функции Кирхгофа. Изобразите графики зависимости испуска-тельной способности от частоты излучения при той же температуре для абсолютно черного тела и серого тела. Поглоща-тельная способность серого тела = 0, 2.

 

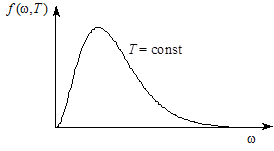
· 15. 13. 2. Абсолютно черное тело имеет температуру Т₁ = 500 К. Какова будет температура Т₂ тела, если в результате нагревания поток излучения увеличится в n = 5 раз?

· 15. 13. 3. Какое количество энергии с площади поверхности S = 1 см² излучает абсолютно черное тело за 1 с, если максимум излучения приходится на длину волны l_m = 4, 84·10^-7 м?

· 15. 13. 4. Расстояние между Солнцем и планетами Земля и Mepкурий соответственно равны: r₁ = 1, 5·10⁸ км, r₂ = 5, 8·10⁷ км. Средняя температура поверхности Земли t _З = 20 ^оС. Принимая Солнце и указанные планеты за абсолютно черные тела, оцените среднюю температуру поверхности Меркурия.

· 15. 13. 5. Абсолютно черное тело имеет температуру Т = 2400 К. До какой температуры охладится тело и насколько изменится максимальное значение испускательной способности тела, если длина волны, на которую приходится максимум испускательной способности, изменится на ∆ l = 9 мкм?

15. 14. Вариант 14

· 15. 14. 1. На рисунке изображен график зависимости испускательной способности от длины волны излучения для некоторого серого тела с поглощательной способностью = 0, 3 для данной температуры. Изо-бразите аналогичную зави-симость для абсолютно черного тела при этой же температуре. Как отличаются энергетические свети-мости этих тел?

· 15. 14. 2. Найдите пло-щадь излучающей поверх-ности нити 25-ваттной лампы, если температура нити равна 2450 К. Излучение нити составляет 30 % излучения абсолютно черного тела при данной температуре. Потерями энергии, связанными с теплопроводностью, можно пренебречь.

· 15. 14. 3. При переходе от температуры Т₁ к температуре Т₂ площадь, ограниченная графиком функции распределения плотности энергии равновесного излучения по длинам волн, увеличивается в 16 раз. Как изменяется при этом длина волна l_m, на которую приходится максимум испускательной способности абсолютно черного тела?

· 15. 14. 4. Шарик диаметром d = 1, 2 см поместили в сосуд, из которого откачан воздух, температура сосуда поддерживается близкой к абсолютному нулю. Начальная температура шарика Т₀ = 300 К. Считая поверхность шарика абсолютно черной, найдите, через какое время его температура уменьшится в n = 2 раза. Плотность материала шарика r = 7·10³ кг/м³, теплоемкость С = 300 Дж·кг^-1·К^–1.

· 15. 14. 5. Максимум испускательной способности абсолютно черного тела сместился с l₁ = 1, 9 мкм до l₂ = 0, 5 мкм. Как изменилась при этом энергетическая светимость и спектральная излучательная способность тела?

15. 15. Вариант 15

· 15. 15. 1. Какие основные теоретические рассуждения легли в основу вывода формулы Планка? Чему равна энергетическая светимость абсолютно черного тела, вычисленная по формуле Планка?

· 15. 15. 2. Найдите температуру нити лампы, мощность которой равна 25 Вт, если площадь излучающей поверхности нити S = 0, 4 см², а поглощательная способность нити a _{w, T} = 0, 3.

· 15. 15. 3. Волосок лампы накаливания, рассчитанный на напряжение U = 2 В, имеет длину = 10 см и диаметр d = 0, 03 мм. Полагая, что волосок излучает как абсолютно черное тело, определите температуру нити и длину волны, на которую приходится максимум энергии в спектре излучения. Удельное сопротивление материала волоска r = 5, 5·10^–8 Ом·м, а потери вследствие теплопроводности пренебрежимо малы.

· 15. 15. 4. В черный тонкостенный металлический сосуд, имеющий форму куба, налита вода массой 1 кг при температуре t₁ = 50 °С, целиком заполняющая сосуд. Определите время остывания сосуда до температуры t₂ = 10 °С, если сосуд помещен в черную полость, температура стенок которой близка к абсолютному нулю.

· 15. 15. 5. Определите энергетическую светимость абсолютно черного тела в интервале длин волн, соответствующим видимой части спектра (l = 0, 4÷ 0, 8 мкм). Примите, что среднее значение испускательной способности тела в этом интервале соответствует значению, найденному для l = 0, 6 мкм. Температура абсолютно черного тела равна 2000 К.

15. 16. Вариант 16

· 15. 16. 1. Для некоторого условного тела испускательная способность задана функцией

 

где Р – постоянная величина. Найдите энергетическую светимость тела.

· 15. 16. 2. Определите поглощательную способность  серого тела, для которого температура, измеренная радиационным пирометром, Т_р = 1, 4 кК, тогда как истинная температура Т = 3, 2 кК.

· 15. 16. 3. Во сколько раз уменьшается мощность излучения абсолютно черного тела при увеличении его температуры от 500 до 1000 K? Определите длины волн, на которые приходится максимум энергии излучения при этих температурах.

· 15. 16. 3. Расстояние между Солнцем и планетами Земля и Марс соответственно равны: r₁ = 1, 5·10⁸ км, r₂ = 2, 3·10⁸ км. Средняя температура поверхности Земли t _З = 20 ^оС. Принимая Солнце и указанные планеты за абсолютно черные тела, оцените среднюю температуру поверхности Марса.

· 15. 16. 5. Определите температуру поверхности Солнца, принимая. его за абсолютно черное тело, если известно, что максимум интенсивности спектра Солнца лежит вблизи l_m = 5·10^–5 см. Чему равно максимальное значение испускательной способности, соответствующее найденной температуре?

15. 17. Вариант 17

· 15. 17. 1. В чем суть «ультрафиолетовой катастрофы», о которой говорили физики, в начале XX в.? Какие допущения предложил Планк, чтобы выйти из «ультрафиолетовой катастрофы»?

· 15. 17. 2. При работе 25-ваттной лампы накаливания на переменном токе (ν = 50 Гц) наибольшая и наименьшая температуры нити отличаются на ∆ t = 70 ^оС. Принимая среднюю температуру нити равной 2450 К, определите относительное изменение за полупериод лучистого потока (мигание лампы).

· 15. 17. 3. При какой температуре максимум спектральной плотности энергетической светимости абсолютно черного тела приходится на длину волн 0, 642 мкм? Найдите энергетическую светимость абсолютно черного тела при этой температуре.

· 15. 17. 4. Тело массой 10 г, площадью поверхности 200 см², имеющее температуру 600 К, помещено в вакуум. Определите, до какой температуры охладится тело за 30 с, если поглощательная способность поверхности тела равна 0, 4, а удельная теплоемкость составляет 335 Дж·кг^–1·К^–1. Лучистым потоком, падающим на тело вследствие излучения окружающих предметов, можно пренебречь.

· 15. 17. 5. Длина волны, на которую приходится максимум испускательной способности абсолютно черного тела, сместилась с 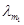= 0, 7 мкм на = 0, 1 мкм. Как и во сколько раз изменилась при этом энергетическая светимость тела и максимальное значение испускательной способности тела?

15. 18. Вариант 18

· 15. 18. 1. На рисунке изображен график зависимости испускательной способности абсолютно черного тела от частоты излучения. Нарисуйте в этих же осях координат аналогич-ный график для серого тела, имеющего при этой же температуре поглощательную способность а _Т = 0, 5. Как отличаются энер-гетические светимости этих тел и частоты, на которые приходятся максимумы испускательных способностей тел?

· 15. 18. 2. Какую мощность нужно подводить к свинцовому шарику радиусом 4 см, чтобы поддерживать его температуру при t₁ = 27 ^оC, если температура окружающей среды t₂ = 23 ^оС. Считайте, что энергия теряется только вследствие излучения. Поглощательная способность свинца равна 0, 6.

· 15. 18. 3. Энергетическая светимость абсолютно черного тела R_э = 250 кВт·м^-2. На какую длину волны приходится максимум испускательной способности этого тела?

· 15. 18. 4. В излучении Солнца, прошедшем через атмосферу и достигнувшем поверхности Земли, максимум испускательной способности приходится на длину волны l_m = 0, 55 мкм. Определите массу, теряемую Солнцем за одни сутки за счет излучения, считая Солнце абсолютно черным телом.

· 15. 18. 5. Температура абсолютно черного тела Т = 3 кК. Определите длину волны l_m, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости для этой длины волны.

Поделиться:

Воспользуйтесь поиском по сайту: