 |
Оптически активные вещества.
|
|
|
|
Оптически активными называются вещества, после прохождения через которые плоскость поляризации линейно поляризованного света поворачивается на некоторый угол (φ) (рис.3).

Рис.3. Поворот плоскости поляризации в оптически активном веществе.
Для определенной длины волны угол поворота плоскости РР' прямо пропорционален толщине слоя вещества d, пройденного светом:
φ = α·d (град) (2)
где α - коэффициент пропорциональности, называемый постоянной вращения. Постоянная вращения зависит от природы вещества, температуры и длины волны света. Зависимость постоянной вращения от длины волны называется вращательной дисперсией. В растворах постоянная вращения прямо пропорциональна концентрации (С) оптически активного вещества, т.е. a=[a]C, и
φ=[α]·С·d (град) (3)
где [α] - удельная постоянная вращения вещества, (град-см2/г). Т.е. удельная постоянная вращения вещества численно равна углу поворота плоскости поляризации, при прохождении светом слоя единичной толщины с единичной концентрацией оптически активного вещества. Соотношение (3) выражает закон Био.
Оптически активные вещества существуют в двух модификациях - правовращающей и левовращающей. Если смотреть навстречу распространению световой волны, то в правовращающих веществах плоскость поляризации поворачивается вправо (по часовой стрелке). Постоянные вращения для правовращающей и левовращающей модификации одного и того же вещества одинаковы.
Основы теории вращения плоскости поляризации.
Любая линейно поляризованная волна может рассматриваться как суперпозиция двух поляризованных по кругу волн с правым и левым направлением вращения светового вектора, т.е. Еп и Ел, соответственно. Френель впервые предположил, что вращение плоскости поляризации линейно поляризованного света можно объяснить, если допустить, что в оптически активной среде монохроматические волны правой и левой круговой поляризации имеют различные фазовые скорости и, следовательно, различные показатели преломления, т.к. фазовая скорость (V) связана с показателем преломления (n) выражением:
|
|
|
V=С/n
где С - скорость света в вакууме.
Рассмотрим линейно поляризованную волну как суперпозицию двух векторов Еп и Ел, которые с течением времени вращаются с одинаковой частотой вправо и влево. (Рис. 4а). Пусть в заданный момент времени t = 0, результирующий вектор Ер (о) = Еп (0) + Ел (0) в точке пространства z = 0 был направлен вдоль оси OY (см. рис.4). На расстоянии z = d вектора Еп (0) и Ел (0) повернутся по отношению к их положению в точке Z = 0соответственно на углы:
δ1=ω·d/Vп; δ2=ω·d/Vл.
где Vп, Vл - скорости волн, поляризованных по правому и левому кругу соответственно, d/Vп, d/Vл - время распространения этих волн на расстояние d. Следовательно, из-за разности скоростей Vп и Vл, между векторами Еп (0) и Ел (0) в точке z = dвозникает разность фаз.
δ=δ1-δ2=ω·d·(1/Vп–1/Vл)

Рис.4. Сложение волн поляризованных по правому и левому кругу:
а) на входе в оптически активное вещество, б) после прохождения в оптически активном веществе пути равного d.
Результирующий вектор E’p (0), как видно из рис.4, при этом повернется на угол d /2, т.е. при прохождении волной расстояния d плоскость поляризации повернется на угол
φ=δ/2=ω·d/2·(1/Vп-1/Vл) (4)
Используя соотношения:
ω = 2p·С/λ; Vп=C/nп; Vл = С/nл
где λ - длина волны в вакууме, nп и nл соответствующие показатели преломления, формулу (4) можно переписать в виде:
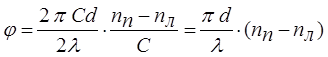 .
.
Таким образом, получим:
 (5)
(5)
Причины различия скоростей волн, поляризованных по правому и левому кругу, в оптически активных веществах связаны с асимметричным строением молекул.
|
|
|
|
|
|


