 |
Теоретические пояснения к теме
|
|
|
|
Метод анализа иерархий (МАИ) является одним из универсальных методов оптимизации, используемых в логистике. Преимуществом МАИ над большинством существующих методов является четкое выражение суждений экспертов и лиц, принимающих решение, а также ясное представление структуры проблемы: элементов и взаимозависимостей между ними. Метод анализа иерархий опирается на достаточно простые элементы, которые оцениваются в шкале МАИ в виде суждений экспертов. А затем на основании обработки экспертных оценок определяется относительная степень их взаимного влияния в иерархии.
Цель, критерии оценивания и альтернативы образуют иерархическую структуру (рис. 1).





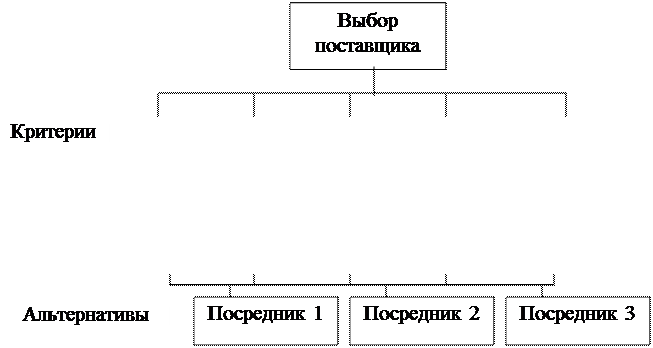
Рисунок 1. Иерархия проблем выбора
Общая цель (фокус) проблемы (например, выбор наилучшего поставщика) является высшим уровнем иерархии. За фокусом следует уровень наиболее важных критериев. Каждый из критериев может разделяться на субкритерии. За субкритериями следует уровень альтернатив, число которых может быть достаточно большим.
Метод анализа иерархий включает в себя парные сравнения, разработку шкалы для преобразования суждений в числовые значения, использование обратно симметричных отношений.
Парные сравнения факторов и альтернатив проводятся в терминах доминирования одного из элементов над другим. Эти суждения в шакале МАИ выражаются в целых числах. Если элемент А доминирует над элементом В, то клетка квадратной матрицы, соответствующая строке А и столбцу В, заполняется целым числом, а клетка, соответствующая строке В и столбцу А, обратным ему числом. Если А и В эквивалентны, то в обе позиции записывается 1.
Обработка результатов в МАИ осуществляется на базе методов матричного анализа с использованием ряда специальных процедур оценки предпочтений на основании специальной шкалы (таблица 1). Это означает, что вначале осуществляется соотношение показателей между собой, а затем расчет веса факторов.
|
|
|
Таблица 1. Шкала отношений МАИ
| Степень важности | Определение | Пояснение |
| Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели | |
| Некоторое преобладание значимости одного действия (показателя фактора) перед другим, слабая зависимость - незначительное предпочтение | Опыт и суждения дают легкое предпочтение одному действию перед другим | |
| Существенное предпочтение или сильная значимость | Опыт и суждения дают сильное предпочтение одному действию перед другим | |
| Очень сильная значимость или очевидное предпочтение | Предпочтение одного действия перед другим очень сильно, его превосходство практически явно | |
| Абсолютное предпочтение | Свидетельство в пользу предпочтения одного действия другому в высшей степени убедительно | |
| 2, 4, 6, 8 | Промежуточные значения между соседними значениями шкалы | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных чисел | Если действию i при сравнении с j присваивается одно из приведенных выше чисел, то действию j по сравнению с i присваивается обратное значение | Если над диагональю находится целое число, то под диагональю – его обратное значение |
| Рациональное значение | Отношение, возникающее в заданной шкале | Для получения согласованной матрицы требуется n числовых значений |
Для обоснования шкалы МАИ учитывается, что способность человека производить количественные разграничения можно представить пятью определениями: а) равный; б) слабый; в) сильный; г) очень сильный; д) абсолютный. Можно принять компромиссные определения между отмеченными соседними, когда нужна большая точность. В целом требуется девять значений, выносимых при сравнении суждений. Использование единицы в начале шкалы соответствует отношению значимости объекта относительно самого себя.
|
|
|
Для определения точности действий необходимо провести расчет показателей согласованности. Отклонение от согласованности называют индексом согласованности (ИС):

При оценивании величины порога несогласованности суждений для матриц размером от одного до пятнадцати методом имитационного моделирования были получены оценки случайного индекса (СИ). СИ является индексом согласованности для сгенерированных случайным образом величин по шкале от одного до девяти положительной обратно симметрической матрицы. В таблице 2 приведены средние (модельные) значения СИ для матриц порядка n = 1:15.
Таблица 2. Случайные индексы
| n | |||||||||||||||
| СИ | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,48 | 1,56 | 1,57 | 1.59 |
Отношение ИС к среднему СИ для матрицы суждений того же порядка называется отношением согласованности (ОС).

Значение ОС ≤0,10 считается приемлемым порогом допустимой согласованности суждений. Если ОС ≥0,1, то необходимо уточнить данные в той или иной матрице суждений.
Первым этапом решения любой задачи (выбора поставщика, определения места расположения склада и др.) является построение иерархии, как показано на рисунке 1. Затем определяется вес элементов на первом уровне иерархии. Для каждого из этих элементов строится матрица векторов-столбцов элементов, находящихся на следующем уровне иерархии. Векторы весов элементов используются для взвешивания собственных векторов-столбцов. Перемножением матрицы векторов на вектор-столбец весов рассчитывают общий вектор весов элементов нижнего уровня. Расчеты необходимо проводить в матричной форме. При этом должно соблюдаться свойство обратной симметрии.
Сравнение следует осуществлять на основе шкалы отношений (таблица 1).
Для определения значений суждений следует начинать с левого элемента матрицы постановкой вопроса, насколько он важнее элемента, расположенного вверху. В случае сравнения элемента с самим собой отношение равно единице. Когда первый элемент важнее второго, используется целое число из шкалы; в противоположном случае берется обратная величина. Для объединения суждений целесообразно найти среднегеометрическое значение, заключающееся в умножении соответствующих числовых значений в матрице суждений и извлечении корня степени, равной числу оцениваемых факторов. Полученный в результате этого столбец нормализуется, и получается вектор приоритета.
|
|
|
После определения вектора приоритета находят оценки согласованности мнений экспертов. Определяется главное значение матрицы -  . Для этого суммируются произведения векторов приоритетов на суммы элементов каждого столбца. Затем определяют отношение согласованности, оно не должно превышать 0,1.
. Для этого суммируются произведения векторов приоритетов на суммы элементов каждого столбца. Затем определяют отношение согласованности, оно не должно превышать 0,1.
|
|
|


